#1 Cách giải bất phương trình bậc 2 chứa tham số hay nhất – Món Miền Trung

Hướng dẫn Cách giải bất phương trình bậc 2 chứa tham số hay nhất, chi tiết, bám sát nội dung SGK Toán lớp 10, giúp các em ôn tập tốt hơn.

1. Bất phương trình bậc hai

– Bất phương trình bậc hai ẩn x là bất phương trình dạng ax2 + bx + c < 0 ( hoặc ax2 + bx + c ≤ 0, ax2 + bx + c > 0, ax2 + bx + c ≥ 0 ), trong đó a, b, c là những số thực đã cho, a ≠ 0 .

* Ví dụ: x2 – 2 >0; 2×2 +3x – 5 <0;

– Giải bất phương trình bậc hai ax2 + bx + c < 0 thực ra là tìm những khoảng chừng mà trong đó f ( x ) = ax2 + bx + c cùng dấu với thông số a ( trường hợp a < 0 ) hay trái dấu với thông số a ( trường hợp a > 0 ) .

2. Dấu của tam thức bậc hai

Nhận xét :

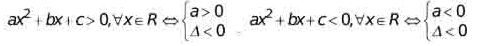
* Định lý : Cho f ( x ) = ax2 + bx + c, Δ = b2 – 4 ac .
– Nếu Δ < 0 thì f ( x ) luôn cùng dấu với thông số a với mọi x ∈ R . – Nếu Δ = 0 thì f ( x ) luôn cùng dấu với thông số a trừ khi x = - b / 2 a . – Nếu Δ > 0 thì f ( x ) luôn cùng dấu với thông số a khi x < x1 hoặc x > x2 ; trái dấu với thông số a khi x1 < x < x2 trong đó x1, x2 ( với x1 < x2 ) là hai nghiệm của f ( x ) .

3. Cách xét dấu của tam thức bậc 2

– Tìm nghiệm của tam thức
– Lập bảng xét dấu dựa vào dấu của thông số a
– Dựa vào bảng xét dấu và Tóm lại

4. Giải bất phương trình bậc 2

– Giải bất phương trình bậc hai ax2 + bx + c < 0 thực ra là tìm những khoảng chừng mà trong đó f ( x ) = ax2 + bx + c cùng dấu với thông số a ( trường hợp a < 0 ) hoặc trái dấu với thông số a ( trường hợp a > 0 ) .
Để giải BPT bậc hai ta vận dụng định lí về dấu của tam thức bậc hai .

5. Một số dạng toán thường gặp

Dạng 1 : Giải bất phương trình bậc hai .

Phương pháp:

– Bước 1 : Biến đổi bất phương trình về dạng một vế là tam thức bậc hai, một vế bằng 0 .
– Bước 2 : Xét dấu vế trái của tam thức bậc hai và Kết luận nghiệm .

Dạng 2 : Giải bất phương trình tích .

Phương pháp:

– Bước 1 : Biến đổi bất phương trình về dạng tích những nhị thức bậc nhất và tam thức bậc hai .
– Bước 2 : Xét dấu những nhị thức bậc nhất và tam thức bậc hai ở trên và Kết luận nghiệm .

Dạng 3 : Giải bất phương trình chứa ẩn ở mẫu

Phương pháp:

– Bước 1 : Biến đổi bất phương trình đã cho về dạng tích, thương những nhị thức bậc nhất và tam thức bậc hai .
– Bước 2 : Xét dấu những nhị thức bậc nhất và tam thức bậc hai ở trên và Kết luận nghiệm .
Chú ý : Cần chú ý quan tâm điều kiện kèm theo xác lập của bất phương trình .

Dạng 4 : Tìm điều kiện kèm theo của tham số để bất phương trình vô nghiệm – có nghiệm – nghiệm đúng

Phương pháp:

Sử dụng 1 số ít đặc thù :
– Nếu Δ < 0 thì tam thức bậc hai cùng dấu với aa . – Bình phương, căn bậc hai, giá trị tuyệt đối của một biểu thức luôn không âm .

Dạng 5 : Giải hệ bất phương trình bậc hai

Phương pháp:

– Bước 1 : Giải từng bất phương trình có trong hệ .
– Bước 2 : Kết hợp nghiệm và Kết luận .

6. Bài tập tìm hiểu thêm có hướng dẫn

Bài 1: Tìm m để bất phương trình x2 – 2(m + 1) + m2 + 2m ≤ 0 có nghiệm với mọi x ∈ [0; 1]

Hướng dẫn giải:

Đặt x2 – 2 ( m + 1 ) + mét vuông + 2 m ≤ 0
Vậy bất phương trình có nghiệm đúng với ∀ x ∈ [ 0 ; 1 ]Phương trình f ( x ) = 0 có hai nghiệm thỏa mãn nhu cầu

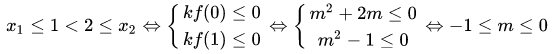
Vậy với – 1 ≤ m ≤ 0 thỏa mãn nhu cầu điều kiện kèm theo đề bài cho .

Bài 2: Tìm m để bất phương trình sau (m + 2)x2 – 2mx + m2 + 2m ≤ 0 có nghiệm.

Hướng dẫn giải

Xét 3 trường hợp :
– Trường hợp 1 : Với m + 2 = 0 ⇒ m = – 2 ta được :
( 1 ) ⇔ 4 x + 4 < 0 ⇔ x < - 1 Bất phương trình vô nghiệm – Trường hợp 2 : Với m < - 2 Bất phương trình đã cho cũng có nghiệm – Trường hợp 3 : m + 2 > 0 ⇒ m > – 2. Khi đó bất phương trình đã cho có nghiệm thì vế trái phải có 2 nghiệm phân biệt :
m > √ 2 và – 2 < m < - √ 2 Vậy với | m | < √ 2 thì bất phương trình có nghiệm .

Bài 3: Tìm m để bất phương trình sau có nghiệm: m2x + 3 <  mx + 4

Hướng dẫn giải:

Bất phương trình tương tự với : m2x – mx < 4 ⇔ ( m2 – m ) x < 1 ; mét vuông – m = 0 ⇔ m = { 0 ; 1 } thì bất phương trình trở thành 0 < 1 đúng với mọi x . Nên bất phương trình có vô số nghiệm .
Vậy bất phương trình có nghiệm với mọi giá trị thực của m .

Bài 4: Tìm tham số m để bất phương trình: f(x) = (m2 + 1)x2 + (2m – 1)x – 5 < 0

Nghiệm đúng với mọi x thuộc khoảng ( -1; 1)

Hướng dẫn giải:

Ta có :

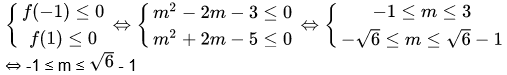
Vậy để bất phương trình có nghiệm đúng với mọi x thuộc khoảng chừng ( – 1, 1 ) thì m ∈ ( – 1 ; √ 6 – 1 )

Source: http://wp.ftn61.com
Category: Hỏi Đáp