Home » Toán Học7 Hằng Đẳng Thức Đáng Nhớ lớp 8 Chi Tiết, Đầy Đủ, Chính XácToán Học

7 Hằng Đẳng Thức Đáng Nhớ lớp 8 Chi Tiết, Đầy Đủ, Chính Xác

7 hằng đẳng thức đáng nhớ là những hằng đẳng thức không còn xa lạ với các bạn nữa, Hôm nay THPT CHUYÊN LAM SƠN sẽ nói kỹ hơn về 7 hằng đẳng thức quan trọng là : bình phương của một tổng, bình phương của một hiệu, hiệu của hai bình phương, lập phương của một tổng, lập phương của một hiệu, tổng hai lập phương và cuối cùng là hiệu hai lập phương.

Chi tiết 7 hẳng đẳng thức đáng nhớ như sau

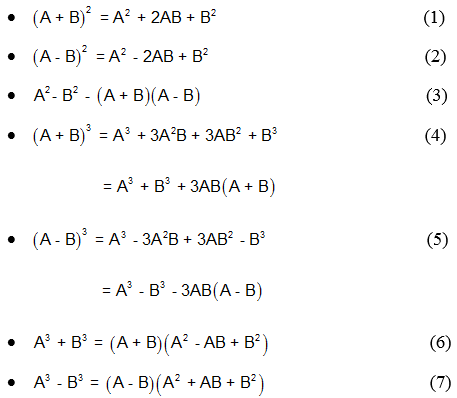
1. Bình phương của một tổng

=> Bình phương của một tổng sẽ bằng bình phương của số thứ nhất cộng hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai .

Ta có 

2. Bình phương của một hiệu

=> Bình phương của một hiệu sẽ bằng bình phương của số thứ nhất trừ đi hai lần tích của số thứ nhất và số thứ hai, sau đó cộng với bình phương của số thứ hai .

Ta có 

3. Hiệu hai bình phương

=> Hiệu của hai bình phương của hai số sẽ bằng hiệu của hai số đó nhân với tổng của hai số đó .

Ta có 

4. Lập phương của một tổng

=> Lập phương của một tổng của hai số sẽ bằng lập phương của số thứ nhất cộng với ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó cộng với lập phương của số thứ hai .

Ta có 

5. Lập phương của một hiệu

=> Lập phương của một hiệu của hai số sẽ bằng lập phương của số thứ nhất trừ đi ba lần tích của bình phương số thứ nhất nhân cho số thứ hai, cộng với ba lần tích của số thứ nhất nhân với bình phương của số thứ hai, rồi sau đó trừ đi lập phương của số thứ hai .

Ta có 

6. Tổng hai lập phương

=> Tổng của hai lập phương của hai số sẽ bằng tổng của số thứ nhất cộng với số thứ hai, sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai .

Ta có 

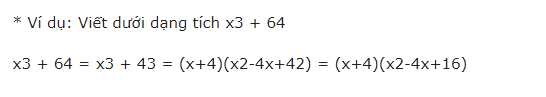
7. Hiệu hai lập phương

=> Hiệu của hai lập phương của hai số sẽ bằng hiệu của số thứ nhất trừ đi số thứ hai, sau đó nhân với bình phương thiếu của tổng số thứ nhất và số thứ hai .

Ta có 

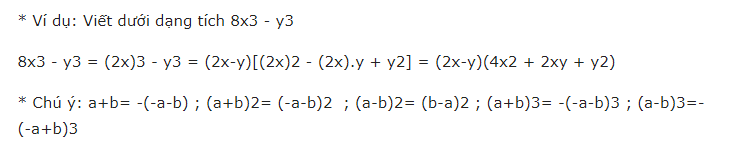
=> Đây là 7 đẳng thức này được sử dụng liên tục trong những bài toán tương quan đến giải phương trình, nhân chia những đa thức, biến hóa biểu thức tại cấp học trung học cơ sở và trung học phổ thông. Học thuộc bảy hằng đẳng thức đáng nhớ giúp giải nhanh những bài toán nghiên cứu và phân tích đa thức thành nhân tử .

Hằng đẳng thức lan rộng ra

Ngoài ra, người ta đã suy ra được những hằng đẳng thức lan rộng ra tương quan đến những hằng đẳng thức trên :

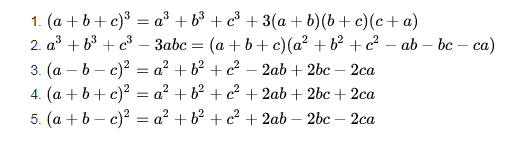
Đây là những hằng đẳng thức rất quan trọng chính vì thế những em cần nhớ rõ trong đầu để mối khi làm bài tập về nhân chia những đa thức, đổi khác biểu thức tại cấp học trung học cơ sở và trung học phổ thông .

Một số bài tập vận dụng bảy hằng đẳng thức đáng nhớ

Dạng 1 : Tính giá trị của biểu thức

Ví dụ : Tính giá trị của biểu thức : A = x2 – 4 x + 4 tại x = – 1
* Lời giải .
– Ta có : A = x2 – 4 x + 4 = x2 – 2. x. 2 + 22 = ( x – 2 ) 2
– Tại x = – 1 : A = ( ( – 1 ) – 2 ) 2 = ( – 3 ) 2 = 9
⇒ Kết luận : Vậy tại x = – 1 thì A = 9

Dạng 2 : Chứng minh biểu thức A không phụ thuộc vào biến

Ví dụ : Chứng minh biểu thức sau không nhờ vào vào x : A = ( x – 1 ) 2 + ( x + 1 ) ( 3 – x )
* Lời giải .
– Ta có : A = ( x – 1 ) 2 + ( x + 1 ) ( 3 – x ) = x2 – 2 x + 1 – x2 + 3 x + 3 – x = 4 : hằng số không phụ thuộc vào vào biến x .

Dạng 3 : Tìm giá trị nhỏ nhất của biểu thức

Ví dụ: Tính giá trị nhỏ nhất của biểu thức: A = x2 – 2x + 5

* Lời giải :
– Ta có : A = x2 – 2 x + 5 = ( x2 – 2 x + 1 ) + 4 = ( x – 1 ) 2 + 4
– Vì ( x – 1 ) 2 ≥ 0 với mọi x .
⇒ ( x – 1 ) 2 + 4 ≥ 4 hay A ≥ 4
– Vậy giá trị nhỏ nhất của A = 4, Dấu “ = ” xảy ra khi : x – 1 = 0 hay x = 1
⇒ Kết luận GTNN của A là : Amin = 4 ⇔ x = 1

Dạng 4 : Tìm giá trị lớn nhất của biểu thức

Ví dụ : Tính giá trị lớn nhất của biểu thức : A = 4 x – x2
* Lời giải :
– Ta có : A = 4 x – x2 = 4 – 4 + 4 x – x2 = 4 – ( 4 – 4 x + x2 ) = 4 – ( x2 – 4 x + 4 ) = 4 – ( x – 2 ) 2
– Vì ( x – 2 ) 2 ≥ 0 với mọi x ⇔ – ( x – 2 ) 2 ≤ 0 với mọi x
⇔ 4 – ( x – 2 ) 2 ≤ 4 [ cộng 2 vế với 4 ] ⇔ A ≤ 4 Dấu “ = ” xảy ra khi : x – 2 = 0 hay x = 2
⇒ Kết luận GTLN của A là : Amax = 4 ⇔ x = 2 .

Dạng 5 : Chứng minh đẳng thức bằng nhau

Ví dụ : Chứng minh đẳng thức sau đúng : ( a + b ) 3 – ( a – b ) 3 = 2 b ( 3 a2 + b2 )
* Lời giải :
– Đối với dạng toán này tất cả chúng ta biến hóa VT = VP hoặc VT = A và VP = A
– Ta có : VT = ( a + b ) 3 – ( a – b ) 3
= ( a3 + 3 a2b + 3 ab2 + b3 ) – ( a3 – 3 a2b + 3 ab2 – b3 )
= a3 + 3 a2b + 3 ab2 + b3 – a3 + 3 a2b – 3 ab2 + b3
= 6 a2b + 2 b3
= 2 b ( 3 a2 + b2 ) = VP ( đpcm ) .
⇒ Kết luận, vậy : ( a + b ) 3 – ( a – b ) 3 = 2 b ( 3 a2 + b2 )

Dạng 7: Phân tích đa thức thành nhân tử

Ví dụ 1 : Phân tích đa thức sau thành nhân tử : A = x2 – 4 x + 4 – y2
* Lời giải :
– Ta có : A = x2 – 4 x + 4 – y2 [ chú ý x2 – 4 x + 4 có dạng hằng đẳng thức ] = ( x2 – 4 x + 4 ) – y2 [ nhóm hạng tử ] = ( x – 2 ) 2 – y2 [ Open đẳng thức số A2 – B2 ] = ( x – 2 – y ) ( x – 2 + y )
⇒ A = ( x – 2 – y ) ( x – 2 + y )

Dạng 8: Tìm giá trị của x

Ví dụ : Tìm giá trị củ x biết : x2 ( x – 3 ) – 4 x + 12 = 0
* Lời giải .
x2 ( x – 3 ) – 4 x + 12 = 0
⇔ x2 ( x – 3 ) – 4 ( x – 3 ) = 0
⇔ ( x – 3 ) ( x2 – 4 ) = 0

⇔ (x – 3)(x – 2)(x + 2) = 0

⇔ ( x – 3 ) = 0 hoặc ( x – 2 ) = 0 hoặc ( x + 2 ) = 0
⇔ x = 3 hoặc x = 2 hoặc x = – 2
⇒ Kết luận, vậy nghiệm : x = 3 ; x = 2 ; x = – 2

Source: http://wp.ftn61.com
Category: Thủ Thuật