Tóm tắt kiến thức toán lớp 11 bài 2: Phương trình lượng giác cơ bản

Dưới đây là bài tóm tắt kiến thức và hướng dẫn giải toán lớp 12 bài 1: Phương trình lượng giác cơ bản, mà các bạn có thể tham khảo để học tốt hơn!

Tóm tắt kiến thức và kỹ năng toán hình lớp 11 bài 2

Với bài này, các bạn cần nắm được các nội dung sau

1. Phương trình sinx = a

Phương trình sinx = a có nghiệm là:

x = a + k2π,          k Bạn đang đọc: Tóm tắt kiến thức toán lớp 11 bài 2: Phương trình lượng giác cơ bản ∈ Z ;    x = π – a + k2π,    k ∈ Z ;

Chú ý :

a) Phương trình sin x = sin βo có các nghiệm là:

x = βo+ k .360 o,k∈ Z ;    x = 180o – βo + k.360o,   k ∈ Z ;

b ) Trong một công thức về nghiệm của phương trình lượng giác không được dùng đồng thời hai đơn vị chức năng độ là radian .
c ) Các trường hợp đặc biệt quan trọng :

a = 1 : Phương trình sinx = 1 có các nghiệm là:

                    x = π/2 + k2π, k ∈ Z

a = –1 : Phương trình sinx = -1 có các nghiệm là:

                    x = –π/2 + k2π, k ∈ Z

a = 0 : Phương trình sinx = 0 có các nghiệm là:

                    x = kπ, k ∈ Z

2. Phương trình cosx = a

Phương trình cosx = a có nghiệm là:

x =±a + k2π, k∈ Z

Chú ý :

a) Phương trình cos x = cos βo có các nghiệm là:

x =±βo+ k .360 o,k∈ Z ;

b ) Các trường hợp đặc biệt quan trọng :

a = 1 : Phương trình cosx = 1 có các nghiệm là:

                    x = k2π, k ∈ Z

a = –1 : Phương trình cosx = -1 có các nghiệm là:

                    x = –π + k2π, k ∈ Z

a = 0 : Phương trình cosx = 0 có các nghiệm là:

                    x = π/2 + kπ, k ∈ Z

3. Phương trình tanx = a

Phương trình tanx = a có nghiệm là:

x =arctana + kπ, k∈ Z

Chú ý :

Phương trình tan x = tan βo có các nghiệm là:

x = βo+ k .180 o,k∈ Z ;

4. Phương trình cotx = a

Phương trình cot x = a có nghiệm là:

x =arctana + kπ, k∈ Z

Chú ý :

Phương trình cot x = cot βo có các nghiệm là:

x = βo+ k .180 o,k∈ Z ;

Hướng dẫn giải bài tập toán lớp 11 bài 2

Bài tập trong sách : ( sgk / 28 )

Câu 1 :

Giải những phương trình sau :

a) sin(x + 2) = 1/3 ;                          b) sin3x = 1 ;

c) sin(2x/3 – π/3) = 0 ;                      d) sin(2x + 20o) = √3/2

Lời giải :

a) sin(x + 2) = ⅓

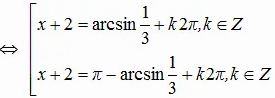
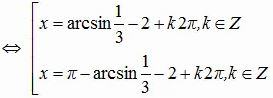
b) sin3x = 1

⇔ sin3x = sin3(π/2)

⇔ 3x = π/2 + k2π  (k ∈ Z)

⇔ x = π/6 + k2π/3  (k ∈ Z)

c) sin(2x/3 – π/3) = 0

⇔ 2x/3 – π/3 = kπ  (k ∈ Z)

⇔ 2x/3 = π/3 + kπ

⇔ x = π/2 + 3kπ/2  (k ∈ Z)

d) sin(2x + 20o) = √3/2

⇔ sin(2x + 20o) = sin(-60o)

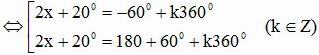
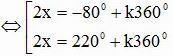
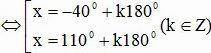
Câu 2: 

Với những giá trị nào của x thì giá trị của các hàm số y = sin 3x và y = sin x bằng nhau?

Lời giải :

Ta có: sin 3x = sin x

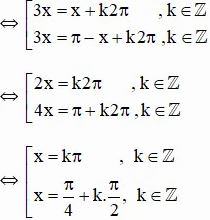
Vậy với x ∈ { kπ ; π / 4 + kπ / 2 } ( k ∈ Z ) thì sin x = sin 3 x

Câu 3: 

Giải những phương trình sau :

a) cos(x – 1) = 2/3 ;                           b) cos3x = cos12o ;

c) cos(3x/3 – π/4) = -1/2 ;                  d) cos22x = 1/4

Lời giải :

a) cos(x – 1) = ⅔

⇔ x – 1 = ± arccos⅔ + k2π ( k ∈ Z )
⇔ x = 1 ± arccos⅔ + k2π
Vậy phương trình có họ nghiệm :
x = 1 ± arccos⅔ + k2π ( k ∈ Z )

b) cos3x = cos12o

⇔ 3 x = ± 12 o + k360o ( k ∈ Z )
⇔ x = 4 o + k120o
Vậy phương trình có họ nghiệm :
x = 4 o + k120o ( k ∈ Z )

c) cos(3x/3 – π/4) = -½

⇔ cos(3x/3 – π/4) = cos(2π/3)

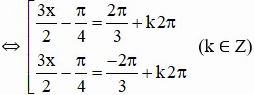
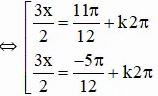
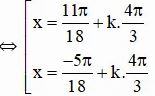
Vậy phương trình có hai họ nghiệm :

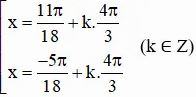
d) cos22x = ¼

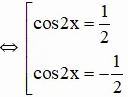
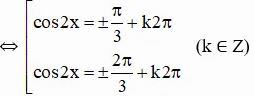
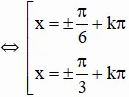
Vậy phương trình có bốn họ nghiệm :

Câu 4:

Giải phương trình

Lời giải :

Điều kiện: sin2x ≠ 1

Ta có :

⇔ 2 cos 2 x = 0
⇔ cos 2 x = 0
⇔ 2 x = π / 2 + kπ ( k ∈ Z )
⇔ x = π / 4 + kπ / 2
Với k = 2 n
⇒ x = π / 4 + n. π
⇒ sin2x = sin ( π / 2 + n. 2 π ) = 1 ∀ n ( TMĐK )
Với k = 2 n + 1
⇒ x = π / 4 + ( 2 n + 1 ) π / 2 = 3 π / 4 + n. π
⇒ sin2x = sin ( 3 π / 2 + n. 2 π ) = – 1 ∀ n ( khôngTMĐK )
Vậy phương trình có họ nghiệm : x = 3 π / 4 + n. π ( n ∈ Z )

Câu 5:

Giải những phương trình sau :

a) tan(x – 15o) = √3/3 ;                  b) cot(3x – 1) = -√3 ;

c) cos2x tanx = 0 ;                           d) sin3x cotx = 0

Lời giải :

a) tan(x – 15o) = √3/3 (ĐK: x – 15 ≠ k.180o  ∀ k ∈ Z)

⇔ x – 15o = 30o + k180o,  k ∈ Z

⇔ x = 45o + k180o,  k ∈ Z

Vậy phương trình có họ nghiệm: x = 45o + k180o  (k ∈ Z)

b) cot(3x – 1) = -√3 (ĐK: 3x – 1 ≠ π/2 + k.π  ∀ k ∈ Z)

⇔ cot ( 3 x – 1 ) = cot ( 5 π / 6 )
⇔ 3 x – 1 = 5 π / 6 + kπ
⇔ x = 1/3 + 5 π / 18 + kπ / 3
Mọi giá trị thuộc họ nghiệm đều thỏa mãn nhu cầu điều kiện kèm theo xác lập
Vậy phương trình có họ nghiệm : x = 1/3 + 5 π / 18 + kπ / 3 k ∈ Z

c) cos2x tanx = 0 

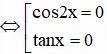
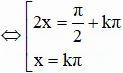
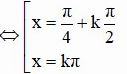
Vậy phương trình có họ nghiệm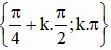

(

k ∈ Z )

d) sin3x cotx = 0 (ĐK: x ≠ k.π với ∀ k ∈ Z)

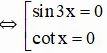
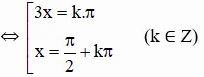
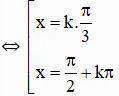
Kết hợp với điều kiện kèm theo ta được :

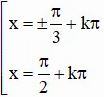
Vậy phương trình có họ nghiệm:

Câu 6:

Với những giá trị nào của x thì giá trị của các hàm số y = tan(π/4 – x) và y = tan2x bằng nhau?

Lời giải :

Ta có: tan(π/4 – x) = tan2x

⇔ 2 x = π / 4 – x + kπ
⇔ 3 x = π / 4 + kπ
⇔ x = π / 12 + kπ / 3 ( k ∈ Z )

Vậy với x = π/12 + kπ/3 thì tan(π/4 – x) = tan2x

Câu 7:

Giải những phương trình sau :

a) sin3x – cos5x = 0 ;                          b) tan3x tanx = 1 ;

Lời giải :

a) sin3x – cos5x = 0

⇔ cos5x = sin3x 

⇔ sin(π/2 – 5x) = sin3x 

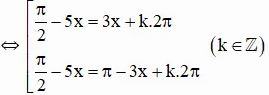
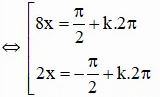
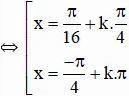
Vậy phương trình có hai họ nghiệm:

(

k ∈ Z )

b) tan3x tanx = 1

( ĐK : 3 x ≠ π / 2 + k. π ; x ≠ π / 2 + k. π ∀ k ∈ Z )

⇔ tan3x = 1/tanx

⇔ tan3x = cotx

⇔ tan3x = tan(π/2 – x)

⇔ 3x = π/2 – x + kπ  (k ∈ Z)

⇔ 4x = π/2 + kπ

⇔ x = π/8 + kπ

Các nghiệm thuộc họ nghiệm trên đều thỏa mãn nhu cầu điều kiện kèm theo

Vậy phương trình có họ nghiệm x = π/8 + kπ (k ∈ Z).

Đó là tóm tắt kiến thức và hướng dẫn giải toán lớp 11 bài 2: Phương trình lượng giác cơ bản, các bạn có thể tham khảo. Đừng quên xem thêm các bài giải toán khác tại chuyên mục : Toán Học lớp 11.

Share this:

• Tweet

• Xem thêm: Một Loại Rau Muống Trong Tiếng Anh Là Gì, Rau Muống In English

We on social :

Facebook

Share this:

• Tweet

Source: http://wp.ftn61.com
Category: Hỏi Đáp