15 câu bài tập Phương trình mũ cơ bản có lời giải chi tiết nhất.

Xin chào các bạn, sau khi hoàn thành bài Phương pháp giải Phương trình mũ chi tiết nhất thì các bạn chắc đã nắm vững được phương pháp giải dạng toán này. Vì vậy hôm nay HocThatGioi sẽ đem đến cho các bạn 15 câu bài tập Phương trình mũ cơ bản giúp các bạn nắm vững kiến thức hơn. Hãy theo dõi hết bài học hôm nay nhé.

1. Cho phương trình 3 ^ { x ^ { 2 } – 4 x + 5 } = 9 tổng lập phương các nghiệm thực của phương trình ?

a. 28

Bạn đang đọc: 15 câu bài tập Phương trình mũ cơ bản có lời giải chi tiết nhất.
b. 27
c. 26
d. 25

Ta có:
3 ^ { x ^ { 2 } – 4 x + 5 } = 9 \ Leftrightarrow 3 ^ { x ^ { 2 } – 4 x + 5 } = 3 ^ { 2 } \ Leftrightarrow x ^ { 2 } – 4 x + 5 = 2 \ Leftrightarrow x = 1 hoặc x = 3
Suy ra 1 ^ { 3 } + 3 ^ { 3 } = 28

2. Cho phương trình 3 ^ { x ^ { 2 } – 3 x + 8 } = 9 ^ { 2 x – 1 }, khi đó tổng các nghiệm của phương trình là ?

a. 5
b. 6
c. 7
d. 8

Ta có:
3 ^ { x ^ { 2 } – 3 x + 8 } = 9 ^ { 2 x – 1 } \ Leftrightarrow 3 ^ { x ^ { 2 } – 3 x + 8 = 3 ^ { 4 x – 2 } } \ Leftrightarrow x ^ { 2 } – 3 x + 8 = 4 x – 2 \ Leftrightarrow x ^ { 2 } – 7 x + 10 = 0 \ Leftrightarrow x = 5 hoặc x = 2.
Vậy tổng các nghiệm 2 + 5 = 7

3. Phương trình 3 ^ { 1 – x } = 2 + ( \ frac { 1 } { 9 } ) ^ { x } có bao nhiêu nghiệm âm ?

a. 0
b. 1
c. 2
d. 3

Phương trình tương đương với \ frac { 3 } { 3 ^ { x } } = 2 + ( \ frac { 1 } { 9 } ) ^ { x } \ Leftrightarrow 3. ( \ frac { 1 } { 3 } ) ^ { x } = 2 + ( \ frac { 1 } { 3 } ) ^ { 2 x } .
Đặt t = ( \ frac { 1 } { 3 } ) ^ { x }, t > 0. Phương trình trở thành
3 t = 2 + t ^ { 2 } \ Leftrightarrow t = {1 ; 2}.
Với t = 1 \ Leftrightarrow ( \ frac { 1 } { 3 } ) ^ { x } = 1 \ Leftrightarrow x = 0.
Với t = 2 \ Leftrightarrow ( \ frac { 1 } { 3 } ) ^ { x } = 2 \ Leftrightarrow x = \ log_ { \ frac { 1 } { 3 } } 2 = – \ log_ { 3 } 2 < 0.
Vậy phương trình có 1 nghiệm âm

4. Số nghiệm của phương trình 9 ^ { \ frac { x } { 2 } } + 9. ( \ frac { 1 } { \ sqrt { 3 } } ) ^ { 2 x + 2 } – 4 = 0 là :

a. 2
b. 4
c. 1
d. 0

Phương trình tương đương với 3 ^ { x } + 3. \ frac { 1 } { 3 ^ { x } } – 4 = 0 \ Leftrightarrow 3 ^ { 2 x } – 4.3 ^ { x } + 3 = 0.
Đặt t = 3 ^ { x }, t > 0. Phương trình trơ thành t ^ { 2 } – 4 t + 3 \ Leftrightarrow t = 1 hoặc t = 3.
Với t = 1 \ Leftrightarrow 3 ^ { x } = 1 \ Rightarrow x = 0.
Với t = 3 \ Leftrightarrow 3 ^ { x } = 3 \ Rightarrow x = 1.
Vậy phương trình có 2 nghiệm

5. Cho phương tình: 2 ^ { | \ frac { 28 } { 3 } x + 4 | } = 16 ^ { x ^ { 2 } – 1 }. Khẳng định nào sau đây đúng ?

a. Tích các nghiệm của phương trình là một số âm.
b. Tổng các nghiệm của phương tình là một số nguyên.
c. Nghiệm của phương trình là các số vô tỉ.
d. Phương trình vô nghiệm.

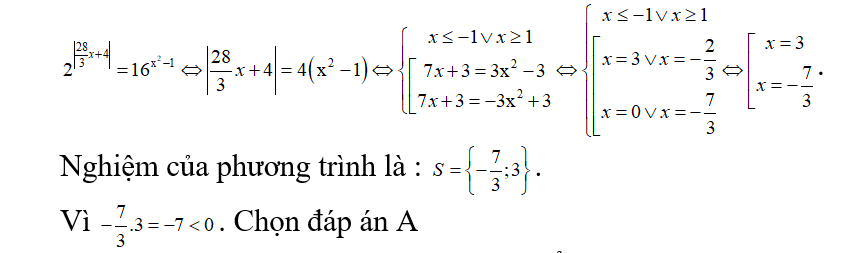
6. Phương trình 2 ^ { 8 – x ^ { 2 } }. 5 ^ { 8 – x ^ { 2 } } = 0,001. ( 10 ^ { 5 } ) ^ { 1 – x } có tổng các nghiệm là :

a. 5
b. 7
c. -7
d. -5

Phương trình đã cho tương đương với ( 2.5 ) ^ { 8 – x ^ { 2 } } = 10 ^ { – 3 }. 10 ^ { 5 – 5 x } \ Leftrightarrow 10 ^ { 8 – x ^ { 2 } } = 10 ^ { 2 – 5 x } \ Leftrightarrow 8 – x ^ { 2 } = 2 – 5 x \ Leftrightarrow x = – 1 ; x = 6.
Ta có : – 1 + 6 = 5

7. Phương trình 9 ^ { x } – 5.3 ^ { x } + 6 – 0 có nghiệm là:

a. x = – 1 ; x = \ log_ { 3 } 2
b. x = 1 ; x = \ log_ { 3 } 2
c. x = 1 ; x = \ log_ { 2 } 3
d. x = – 1 ; x = – \ log_ { 3 } 2

Đặt = 3 ^ { x } ] khi đó phương trình tương đương với:
t ^ { 2 } – 5 t + 6 = 0 \ Leftrightarrow t = 2 ; t = 3.
Với t = 2 \ Leftrightarrow 3 ^ { x } = 2 \ Rightarrow x = \ log_ { 3 } 2
Với t = 3 \ Leftrightarrow 3 ^ { x } = 3 \ Rightarrow x = 1

8. Cho phương trình 4.4 ^ { x } – 9.2 ^ { x + 1 } + 8 = 0. Gọi x_ { 1 }, x_ { 2 } là hai nghiệm phương trình trên. Khi đó x_ { 1 }. x_ { 2 } bằng:

a. -2
b. 2
c. -1
d. 1

Đặt

t = 2^{x}, t > 0

Xem thêm: Một Loại Rau Muống Trong Tiếng Anh Là Gì, Rau Muống In English

khi đó phương trình đã cho tương đương với:
4 t ^ { 2 } – 18 t + 8 = 0 \ Leftrightarrow t = 4 ; t = \ frac { 1 } { 2 } \ Leftrightarrow x_ { 1 } = 2 ; x_ { 2 } = – 1.
Vậy x_ { 1 }. x_ { 2 } = – 2

9. Cho phương trình 4 ^ { x } – 4 ^ { 1 – x } = 3. Khăng định nào sai ?

a. Phương trình có một nghiệm.
b. Nghiệm của phương trình là luôn lớn hơn 0.
c. Phương trình vô nghiệm.
d. Phương trình đã cho tương đương với phương trình 4 ^ { 2 x } – 3.4 ^ { x } – 4 = 0.

Đặt t = 4 ^ { x }, t > 0 khi đó phương trình đã cho tương đương với:
t ^ { 2 } – 3 t – 4 = 0 \ Leftrightarrow t = 4 ; t = – 1 (loại) \ Leftrightarrow x_ { 1 } = 2.

10. Cho phương trình 9 ^ { x ^ { 2 } + x – 1 } – 10.3 ^ { x ^ { 2 } + x – 2 } + 1 = –. Tổng tất cả các nghiệm của phương trình là:

a. -2
b. 2
c. 1
d. 0

Đặt t = 3 ^ { x ^ { 2 } + x – 1 }, t > 0, khi đó phương trình đã cho tương đương với:
3 t ^ { 2 } – 10 t + 3 = 0 \ Leftrightarrow t = 3 ; t = \ frac { 1 } { 3 }
Với t = 3 \ Leftrightarrow 3 ^ { x ^ { 2 } + x – 1 } = 3 \ Leftrightarrow x ^ { 2 } + x – 1 = 1 \ Rightarrow x = 1 hoặc x = – 2
Với t = \ frac { 1 } { 3 } \ Leftrightarrow 3 ^ { x ^ { 2 } + x – 1 } = \ frac { 1 } { 3 } \ Leftrightarrow x ^ { 2 } + x – 1 = – 1 \ Rightarrow x = – 1 hoặc x = – 0
Vậy tổng các nghiệm bằng -2

11. Nghiệm của phương trình 2 ^ { x } + 2 ^ { x + 1 } = 3 ^ { x } + 3 ^ { x + 1 } là:

a. x = \ log_ { \ frac { 3 } { 2 } } \ frac { 3 } { 4 }
b. x = 1
c. x = 0
d. x = \ log_ { \ frac { 4 } { 3 } } \ frac { 2 } { 3 }

Phương trình đã cho tương đương với:
3.2 ^ { x } = 4.3 ^ { x } \ Leftrightarrow ( \ frac { 3 } { 2 } ) ^ { x } = \ frac { 3 } { 4 } \ Rightarrow x = \ log_ { \ frac { 3 } { 2 } } \ frac { 3 } { 4 }

12. Tổng nghiệm của phương tình 2 ^ { 2 x } – 3.2 ^ { x + 2 } + 32 = 0 là

a. 2
b. 3
c. 4
d. 5

Ta có:
2 ^ { 2 x } – 3.2 ^ { x } + 32 = 0 \ Leftrightarrow 2 ^ { 2 x } – 12.2 ^ { x } + 32 = 0 \ Leftrightarrow 2 ^ { x } = 8 ; 2 ^ { x } = 4 \ Leftrightarrow x = 3 ; x = 2

13. Nghiệm của phương trình 6.4 ^ { x } – 13.6 ^ { x } + 6.9 ^ { x } = 0 là:

a. x \ in {1 ; – 1}
b. x \ in {\ frac { 2 } { 3 } ; \ frac { 3 } { 2 }}
c. x \ in {- 1 ; 0}
d. x \ in {0 ; 1}

Phương trình đã cho tương đương với:
6. ( \ frac { 3 } { 2 } ) ^ { x } – 13. ( \ frac { 3 } { 2 } ) ^ { x } + 6 = 0
\ Leftrightarrow ( \ frac { 3 } { 2 } ) ^ { x } = \ frac { 3 } { 2 } ; ( \ frac { 3 } { 2 } ) ^ { x } = \ frac { 2 } { 3 } \ Rightarrow x = \ pm 1

14. Phương trình 9 ^ { x } – 5.3 ^ { x } + 6 = 0 có tổng các nghiệm là:

a. 3
b. \ log_ { 3 } \ frac { 2 } { 3 }
c. 2
d. \ log_ { 3 } 6

Phương trình đã cho tương đương với
( 3 ^ { 2 } ) ^ { x } – 5.3 ^ { x } + 6 \ Leftrightarrow ( 3 ^ { x } ) ^ { 2 } – 5.3 ^ { x } + 6 = 0 \ Leftrightarrow 3 ^ { x } = 2 ; 3 ^ { x } = 3 \ Rightarrow x = \ log_ { 3 } 2 ; x = 1.
Vậy 1 + \ log_ { 3 } 2 = \ log_ { 3 } 6

15. Cho phương trình 2 ^ { 1 + 2 x } + 15.2 ^ { x } – 8 = 0, khẳng định nào sau đây đúng ?

a. Có một nghiệm
b. Vô nghiệm
c. Có hai nghiệm dương
d. Có hai nghiệm âm.

Phương trình đã cho tương đương với

2.2^{2x} + 15.2^{x} – 8 \Leftrightarrow 2^{x} = \frac{1}{2}

Xem thêm: Bộ Kế hoạch Đầu tư Tiếng Anh là gì?

hoặc 2 ^ { x } = – 8 (loại).
Với 2 ^ { x } = \ frac { 1 } { 2 } \ Rightarrow x = – 1

Trên đây là bài viết 15 câu bài tập Phương trĩnh mũ cơ bản có lời giải chi tiết nhất mà HocThatGioi đã đem đến cho các bạn. Qua bài viết này, Các bạn cùng theo dõi các bài viết tiếp theo về chương Hàm số mũ – Hàm số logarit để có một nền tảng thật vững chắc nhé. Cảm ơn các bạn đã theo dõi bài viết của HocThatGioi. Hãy đồng hành cùng HocThatGioi để tiếp thu thêm các kiến thức hay, bổ ích nhé. Chúc các bạn học tốt