Bảng công thức lượng giác chi tiết, dễ hiểu, tải về file pdf

Bảng công thức lượng giác thật sự là một vấn đề khá nan giải đối với các em học sinh “lười học công thức”. Tuy nhiên, học lượng giác mà không nắm rõ công thức thì thật sự rất khó để làm bài tập. Dưới đây là hệ thống lại các công thức lượng giác cần thiết cơ bản, cũng như nâng cao. Chỉ cần nắm vững các công thức dưới đây, các em hoàn toàn có thể giải quyết bài tập một cách nhanh gọn. Hãy tải công thức về ở dạng file pdf sau đó áp dụng những phương pháp học thuộc mà chúng tôi giới thiệu dưới đây nhé!

TẢI XUỐNG PDF ↓



Công thức lượng giác cơ bản và mở rộng

Công thức cơ bản nhất

• \[{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\]
• \[\tan \alpha .\cot \alpha =1\]
• \[1+{{\tan }^{2}}\alpha =\frac{1}{{{\cos }^{2}}\alpha }\]
• \[1+{{\cot }^{2}}\alpha =\frac{1}{{{\sin }^{2}}\alpha }\]

Công thức cộng

• \[\sin (a+b)=\sin a.\cos b+\sin b.\cos a\]
• \[\sin (a-b)=\sin a.\cos b-\sin b.\cos a\]
• \[\cos (a+b)=\cos a.\cos b-\sin a.\sin b\]
• \[\cos (a-b)=\cos a.\cos b+\sin a.\sin b\]

Công thức nhân đôi

• \[\sin 2\alpha =2.\sin \alpha .\cos \alpha \]
• \[\cos 2\alpha ={{\cos }^{2}}\alpha -{{\sin }^{2}}\alpha =2.{{\cos }^{2}}\alpha -1=1-2{{\sin }^{2}}\alpha \]
• \[\tan 2\alpha =\frac{2\tan \alpha }{1-{{\tan }^{2}}\alpha }\]
• \[\cot \alpha =\frac{{{\cot }^{2}}\alpha -1}{2\cot \alpha }\]

Hệ quả công thức hạ bậc bậc hai

• \[{{\sin }^{2}}\alpha =\frac{1-\cos 2\alpha }{2}\]
• \[{{\cos }^{2}}\alpha =\frac{1+\cos 2\alpha }{2}\]
• \[{{\tan }^{2}}\alpha =\frac{1-\cos 2\alpha }{1+\cos 2\alpha }\]

Công thức nhân ba

• \[\sin 3\alpha =3\sin \alpha -4{{\sin }^{3}}\alpha \]
• \[\cos 3\alpha =4{{\cos }^{3}}\alpha -3\cos \alpha \]
• \[\tan 3\alpha =\frac{3\tan \alpha -{{\tan }^{3}}\alpha }{1-3{{\tan }^{2}}\alpha }\]

Hệ quả: Công thức hạ bậc bậc ba:

• \[{{\sin }^{3}}\alpha =\frac{1}{4}.3\sin \alpha -\sin 3\alpha \]
• \[{{\cos }^{3}}\alpha =\frac{1}{4}.3cos\alpha +\cos 3\alpha \]

Công thức biến đổi tổng thành tích

• \[\cos a+\cos b=2\cos \frac{a+b}{2}.\cos \frac{a-b}{2}\]
• \[\cos a-\cos b=-2\sin \frac{a+b}{2}.\sin \frac{a-b}{2}\]
• \[\sin a+\sin b=2.\sin \frac{a+b}{2}.\cos \frac{a-b}{2}\]
• \[\sin a-\sin b=2.\cos \frac{a+b}{2}.\sin \frac{a-b}{2}\]

Công thức biến đổi tích thành tổng

• \[\cos a.\cos b=\frac{1}{2}[\cos (a-b)+cos(a+b)]\]
• \[\sin a.\sin b=\frac{1}{2}[\cos (a-b)-\cos (a+b)]\]
• \[\sin a.\cos b=\frac{1}{2}[\sin (a-b)+\sin (a+b)]\]

Công thức lượng giác biểu diễn theo tan

• \[\sin \alpha =\frac{2t}{1+{{t}^{2}}}\]
• \[\cos \alpha =\frac{1-{{t}^{2}}}{1+{{t}^{2}}}\]
• \[\tan \alpha =\frac{2t}{1-{{t}^{2}}}\]

Công thức lượng giác bổ sung

• \[\cos \alpha \pm \sin \alpha =\sqrt{2}.\cos \left( \alpha \pm \frac{\pi }{4} \right)=\sqrt{2}.sin\left( \frac{\pi }{4}\pm \alpha \right)\]
• \[\sin \alpha \pm \cos \alpha =\sqrt{2}.sin\left( \alpha \pm \frac{\pi }{4} \right)=\sqrt{2}.\cos \left( \frac{\pi }{4}\mp \alpha \right)\]
• \[1+\sin 2\alpha ={{(\cos \alpha +\sin \alpha )}^{2}}\]
• \[\tan \alpha +\cot \alpha =\frac{2}{\sin 2\alpha }\]
• \[\cot \alpha -\tan \alpha =2\cot 2\alpha \]
• \[{{\sin }^{4}}\alpha +{{\cos }^{4}}\alpha =1-\frac{1}{2}{{\sin }^{2}}2\alpha =\frac{1}{4}\cos 4\alpha +\frac{3}{4}\]
• \[{{\sin }^{6}}\alpha +{{\cos }^{6}}\alpha =1-\frac{3}{4}{{\sin }^{2}}2\alpha =\frac{3}{8}\cos 4\alpha +\frac{5}{8}\]

Công thức tổng quát hơn về việc hơn kém pi

Hơn kém bội hai pi của sin và cos và tang, cotang hơn kém bội pi .

• Sin(a+k.2.180) = sin (a+k.2.pi) = sin a
• Cos(a+k.2.180) = cos (a+k.2.pi) = sin a
• Tg(a+k.180) = tga
• Cotg(a+k.180)=cotga

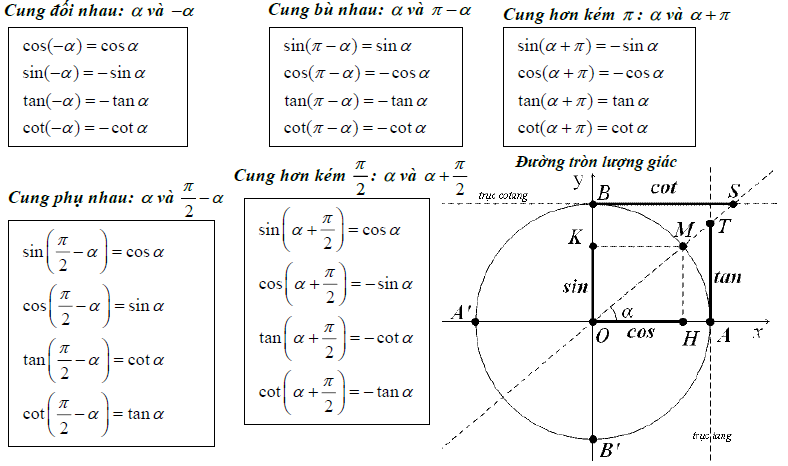
Giá trị lượng giác đặc biệt của các cung liên quan

Cung đối nhau

\ [ \ sin ( – \ alpha ) = – sin \ alpha \ ] \ [ \ cos ( – \ alpha ) = \ cos \ alpha \ ] \ [ \ tan ( – \ alpha ) = – \ tan \ alpha \ ] \ [ \ cot ( – \ alpha ) = – \ cot \ alpha \ ]

Cung bù nhau

• \[\sin (\pi -\alpha )=\sin \alpha \]
• \[\cos (\pi -\alpha )=-\cos \alpha \]
• \[\tan (\pi -\alpha )=-\tan \alpha \]
• \[\cot (\pi -\alpha )=-\cot \alpha \]

Cùng phụ nhau

• \[\sin (\frac{\pi }{2}-\alpha )=\cos \alpha \]
• \[\cos (\frac{\pi }{2}-\alpha )=\sin \alpha \]
• \[\tan (\frac{\pi }{2}-\alpha )=\cot \alpha \]
• \[\cot (\frac{\pi }{2}-\alpha )=\tan \alpha \]

Góc hơn kém nhau pi

• \[\sin (\pi +\alpha )=-\sin \alpha \]
• \[\cos (\pi +\alpha )=-\cos \alpha \]
• \[\tan (\pi +\alpha )=\tan \alpha \]
• \[\cot (\pi +\alpha )=\cot \alpha \]

Góc hơn kém pi/2

• \[\sin \left( \frac{\pi }{2}+\alpha \right)=\cos \alpha \]
• \[\cos \left( \frac{\pi }{2}+\alpha \right)=-\sin \alpha \]
• \[\tan \left( \frac{\pi }{2}+\alpha \right)=-\cos \alpha \]
• \[\cot \left( \frac{\pi }{2}+\alpha \right)=-\tan \alpha \]

Xem thêm : Bảng giá trị lượng giác từ 0 độ đến 360 độ

Học thuộc công thức lượng giác bằng thơ

Bài thơ công thức cộng lượng giác

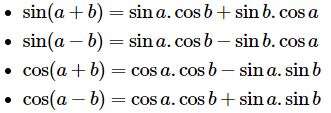
Cos thì cos cos sin sin
Sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi nàng
Sin thì giữ dấu xin chàng nhớ cho !

Bài thơ công thức nhân đôi

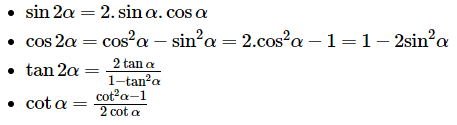
Bài thơ của cos và sin

Sin gấp đôi bằng hai sin cos
Cos gấp đôi bằng bình cos trừ bình sin
Bằng trừ một cộng hai bình cos
Bằng cộng một trừ hai bình sin

Bài thơ của tan

Tang đôi ta lấy đôi tang
Chia 1 trừ lại bình tang, ra liền.

Bài thơ công thức nhân ba

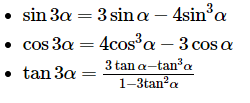
Bài 1

cos 3 x bằng 4 cỏn trừ 3 con
sin 3 x bằng 3 sin trừ 4 sỉn

Bài 2

Nhân ba một góc bất kể ,
sin thì ba bốn, cos thì bốn ba ,
dấu trừ đặt giữa 2 ta, lập phương chỗ bốn ,
… thế là okee

Bài thơ công thức tổng thành tích

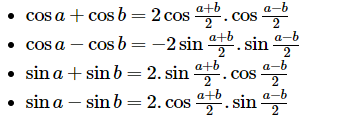
Đối với các hệ số khi khai triển

Cos cộng cos bằng hai cos cos
Cos trừ cos bằng trừ hai sin sin
Sin cộng sin bằng hai sin cos
Sin trừ sin bằng hai cos sin.

Ghi nhớ cho: Tổng chia hai trước, hiệu chia hai sau ( nhớ thứ tự \[\frac{a+b}{2},\frac{a-b}{2}\])

Bài thơ công thức tích thành tổng

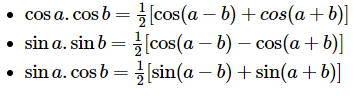
Nhớ rằng hiệu trước, tổng sau
Sin sin, cos tổng phải ghi dấu trừ
Cos thì cos hết
Sin sin cos cos, sin cos sin sin
Một phần hai phải nhân vào, chớ quên

Bài thơ công thức biến đổi theo tan:

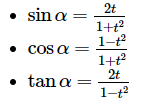
Sin, cos mẫu giống nhau chả khác

Ai cũng là một + bình tê (1+t^2)

Sin thì tử có 2 tê ( 2 t ) ,
cos thì tử có 1 trừ bình tê ( 1 – t ^ 2 ) .

Cách nhớ giá trị lượng giác cung đặc biệt

• Sin bù: Sin(180-a)=sina.
• Cos đối: Cos(-a)=cosa.
• Hơn kém pi tang: Tan(a+180) = tan a.
• Cotg (a+180) = cotga.
• Phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia. Ví dụ tan góc này = cotg góc kia.

Định nghĩa góc và cung lượng giác

Đường tròn định hướng và cung lượng giác

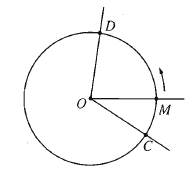
Đường tròn khuynh hướng là một đường tròn trên đó ta đã chọn một chiều hoạt động gọi là chiều dương, chiều ngược lại là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ đeo tay làm chiều dương. Trên đường tròn đó ta cho hai điểm A, B. Một điểm M di động trên đường tròn luôn theo một chiều âm hoặc dương từ A đến B tạo nên một cung lượng giác có điểm đầu là A và điểm cuối B. Theo dõi hình vẽ dưới đây :

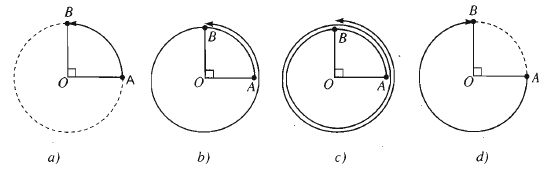
Định nghĩa về góc lượng giác trong các công thức lượng giác

Trên đường tròn cố định và thắt chặt cho một cung lượng giác \ [ \ overset \ frown { CD } \ ]. Một điểm M hoạt động trên đường tròn từ C tới D tạo nên cung lượng giác nói trên. Khi đó tia OM quay xung quanh gốc O từ vị trí OC tới vị trí OD. Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là OD. Kí hiệu góc lượng giác đó là ( OC, OD ) .

Đường tròn lượng giác

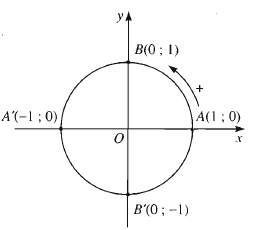
Trong mặt phẳng tọa độ Oxy vẽ đường tròn định hướng tâm O nửa đường kính R = 1. Đường tròn này cắt trục tọa độ tại bốn điểm A ( 1 ; 0 ), A ‘ ( – 1 ; 0 ), B ( 0 ; 1 ), B ‘ ( 0 ; – 1 ). Ta lấy A ( 1 ; 0 ) làm điểm gốc của đường tròn đó. Đường tròn như trên được gọi là đường tròn đường tròn lượng giác gốc A .

So sánh độ và radian

• Đơn vị độ đã được sử dụng để đo góc từ rất lâu đời. Trong toán học và vật lí người ta còn dùng một đơn vị nữa để đo cung, đó là rađian.
• Định nghĩa: Trên một đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số đo 1 rad.
• Quan hệ giữa độ và radia: Bằng một vài chứng minh đơn giản, ta hoàn toàn có thể chứng minh được công thức sau:

Bảng chuyển đổi thông dụng

Số đo của một cung lượng giác

Số đo của một cung lượng giác là một số thực, âm hoặc dương. Số đo lượng giác của những cung có cùng điểm đầu và điểm cuối sai khác nhau một bội số 2 pi. Ta viết :

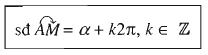
Công thức số đo của một góc lượng giác

Ta định nghĩa : Số đo của một góc lượng giác ( OA, OC ) là số đo của cung lượng giác AC tương ứng .

Vì mỗi cung lượng giác ứng với một góc lượng giác và ngược lại, đồng thời số đo của những cung và góc lượng giác tương ứng là trùng nhau, nên từ nay về sau khi ta nói về cung thì điều đó cũng đúng cho góc và ngược lại .

Biểu diễn cung lượng giác lên đường tròn lượng giác

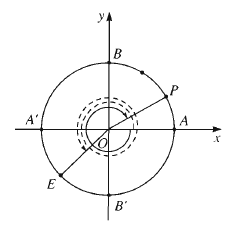
Chọn điểm gốc A ( 1 ; 0 ) làm điểm đầu của toàn bộ những cung lượng giác trên đường tròn lượng giác. Để trình diễn cung lượng giác có số đo anlpha trên đường tròn lượng giác ta cần chọn điểm cuối M của cung này. Điểm cuối M được xác lập bởi hệ thức số đo AM = anlpha

Giá trị lượng giác của cung anlpha

Trên đường tròn lượng giác cho cung \ [ \ overset \ frown { AM } = \ alpha \ ]. Tung độ \ [ y = \ overline { OK } \ ]. Điểm M dược gọi là sin của \ [ \ alpha \ ] và kí hiệu là \ [ \ sin \ alpha \ ]. Hoành độ \ [ x = \ overline { OH } \ ] thì điểm M gọi là cosin của anlpha và được kí hiệu là \ [ \ sin \ alpha \ ] .
\ [ \ sin \ alpha = \ overline { OK } \ ] Các giá trị \ [ \ sin \ alpha ; \ cos \ alpha ; \ tan \ alpha ; \ cot \ alpha \ ] được gọi là những giá trị lượng giác của cung \ [ \ alpha \ ] .
Ta cũng gọi trục tung là trục sin, còn trục hoành là trục cosin .
Các định nghĩa trên được vận dụng cho những góc lượng giác
Nếu \ [ \ alpha \ ] nằm trong khoảng chừng 0 đến 180 độ, thì những giá trị lượng giác của góc \ [ \ alpha \ ] chính là những giá trị lượng giác của góc đó đã nêu trong SGK hình học lớp 10 .
Do đó, ta có một số ít hệ quả sau về công thức lượng giác và giá trị lượng giác tương quan đến góc :

Bảng xác định dấu của các giá trị lượng giác

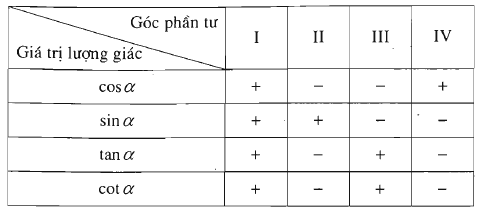
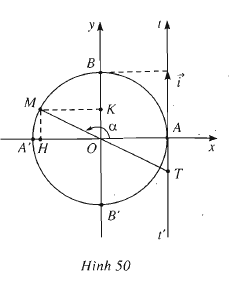
Ý nghĩa hình học của \[\tan \alpha \]

Từ A vẽ tiếp tuyến t’At với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc A và vec tơ đơn vị chức năng …
Cho cung lượng giác AM có số đo là anpla. Gọi T là giao điểm của OM với trục tung t’At. Giả sử T không trùng với A. Vì MH song song với AT, nên ta có
\ [ \ frac { AT } { HM } = \ frac { OA } { OH } \ ] suy ra \ [ \ frac { \ overline { AT } } { \ overline { HM } } = \ frac { \ overline { OA } } { \ overline { OH } } \ ] Vậy, \ [ \ tan \ alpha \ ] được trình diễn bởi độ dài đại số của véc tơ AT trên trục t’At. Trục t’At được gọi là trục tang .

Trắc nghiệm công thức lượng giác

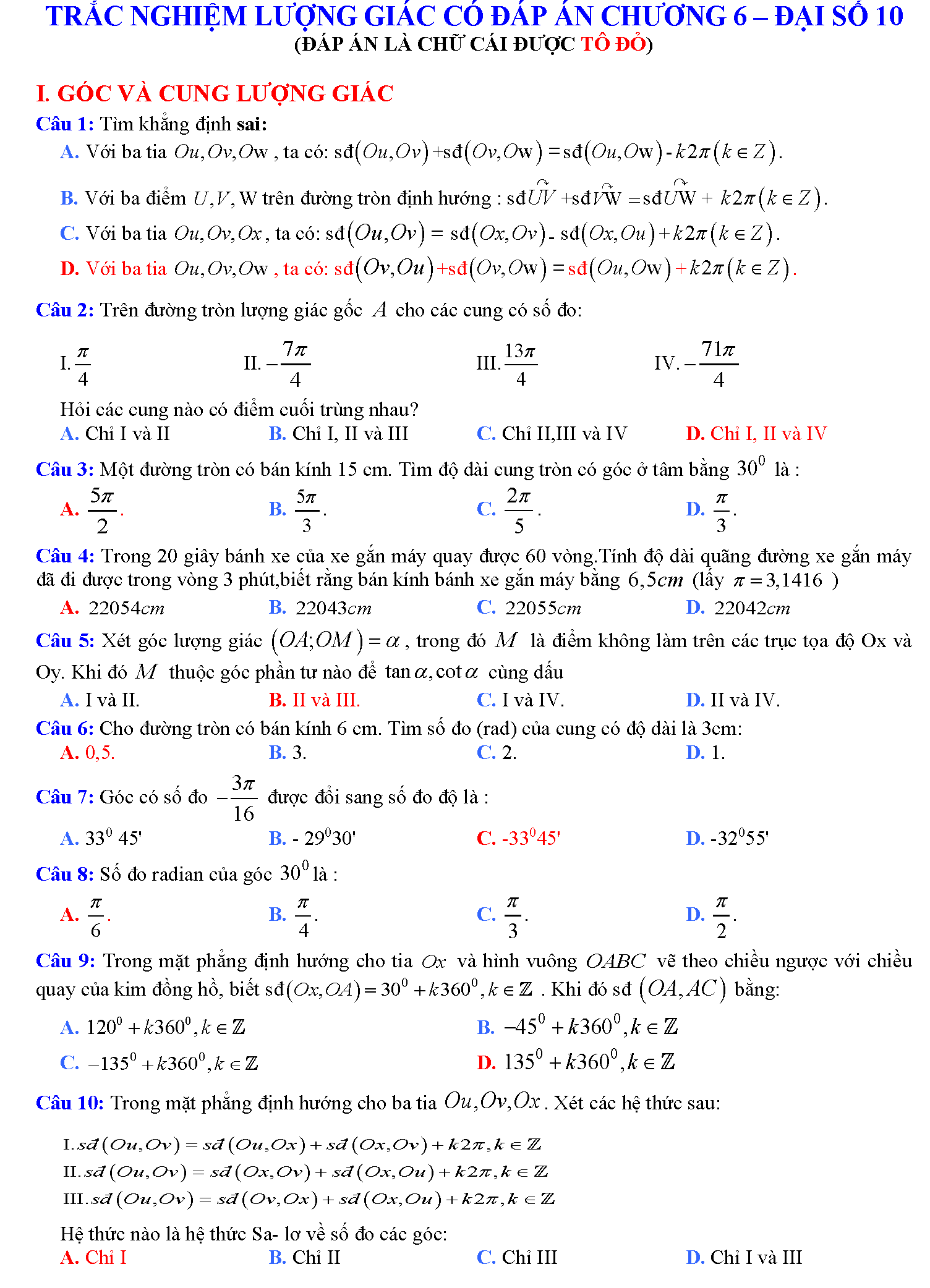
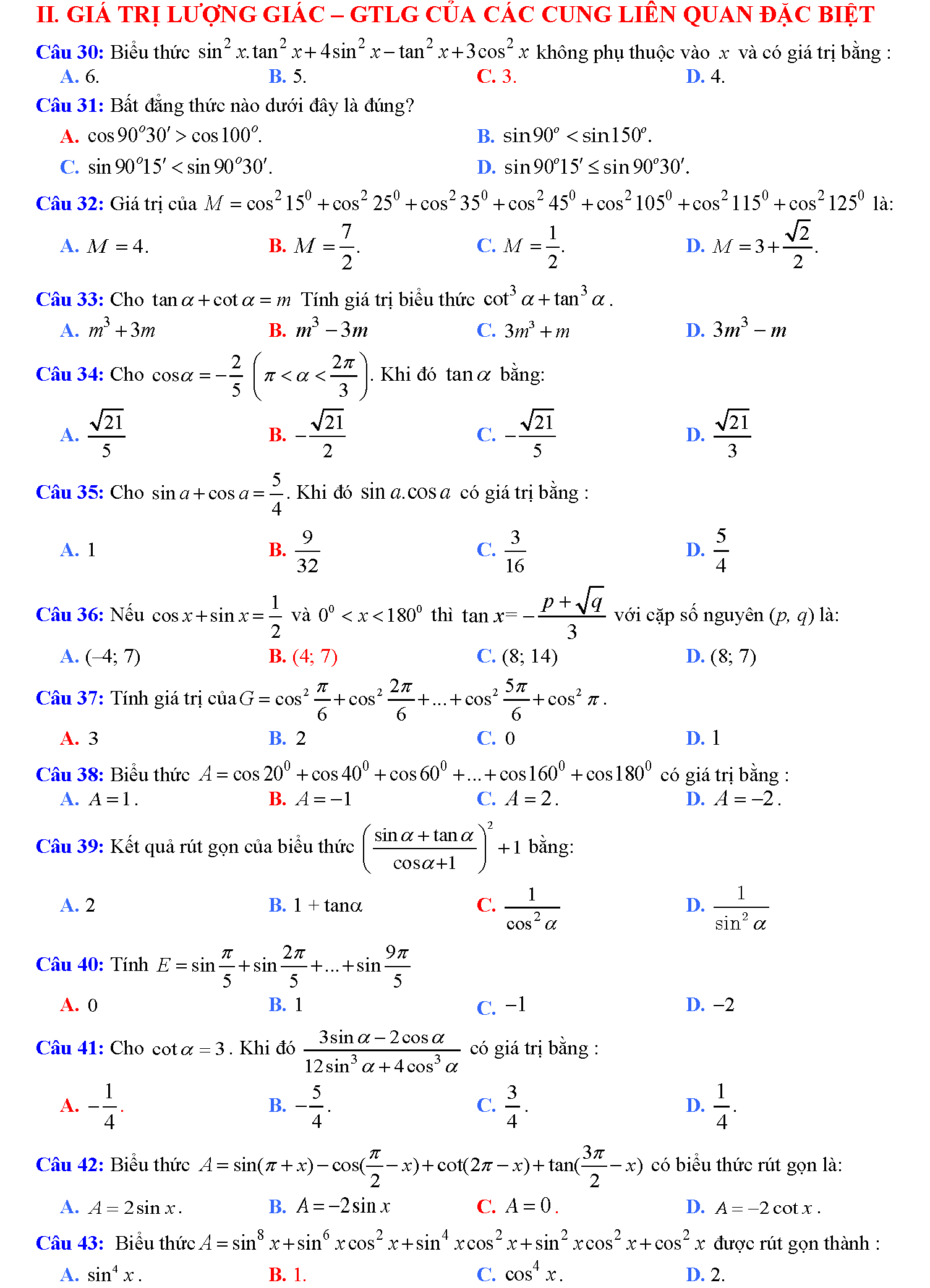
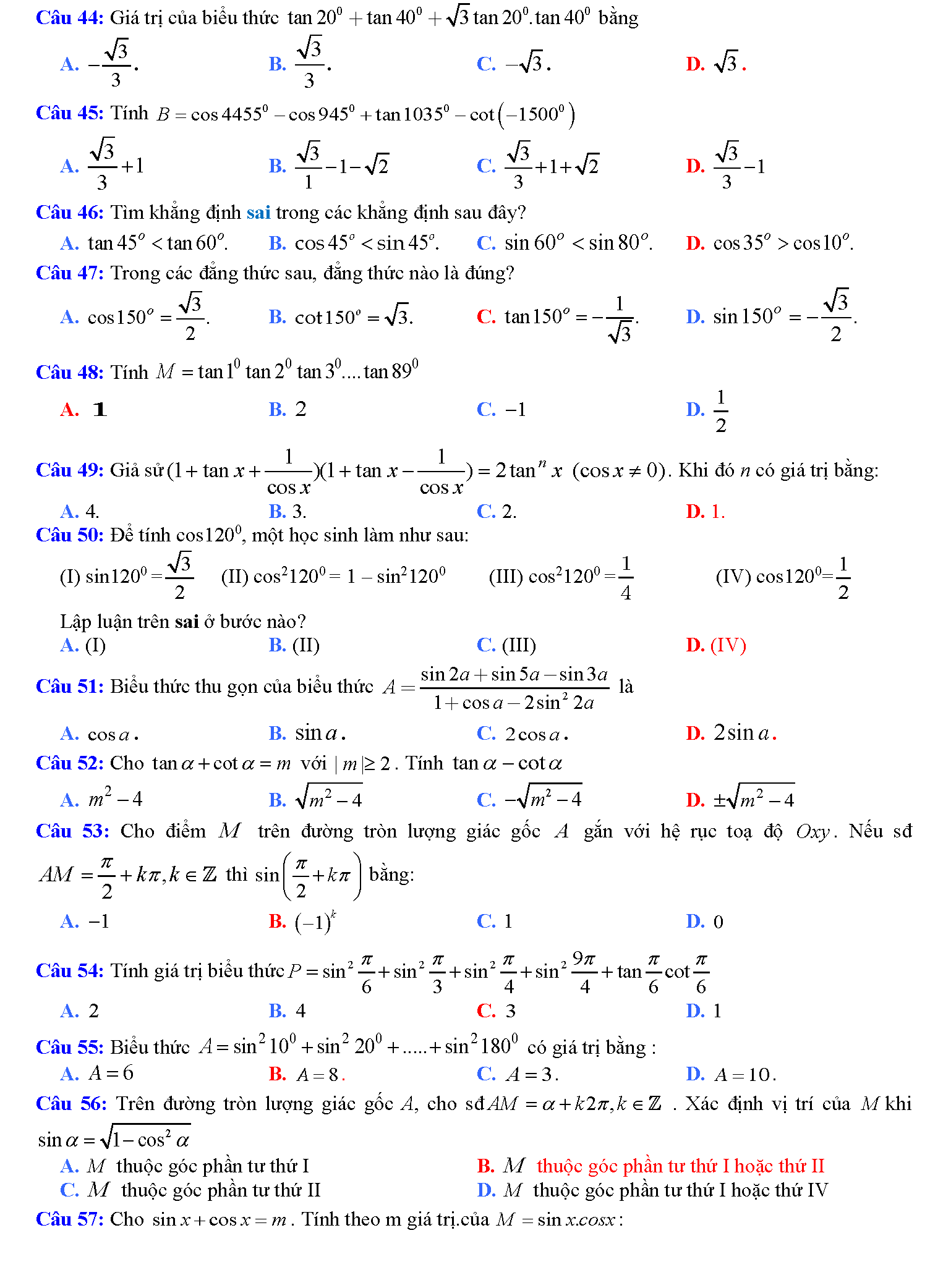
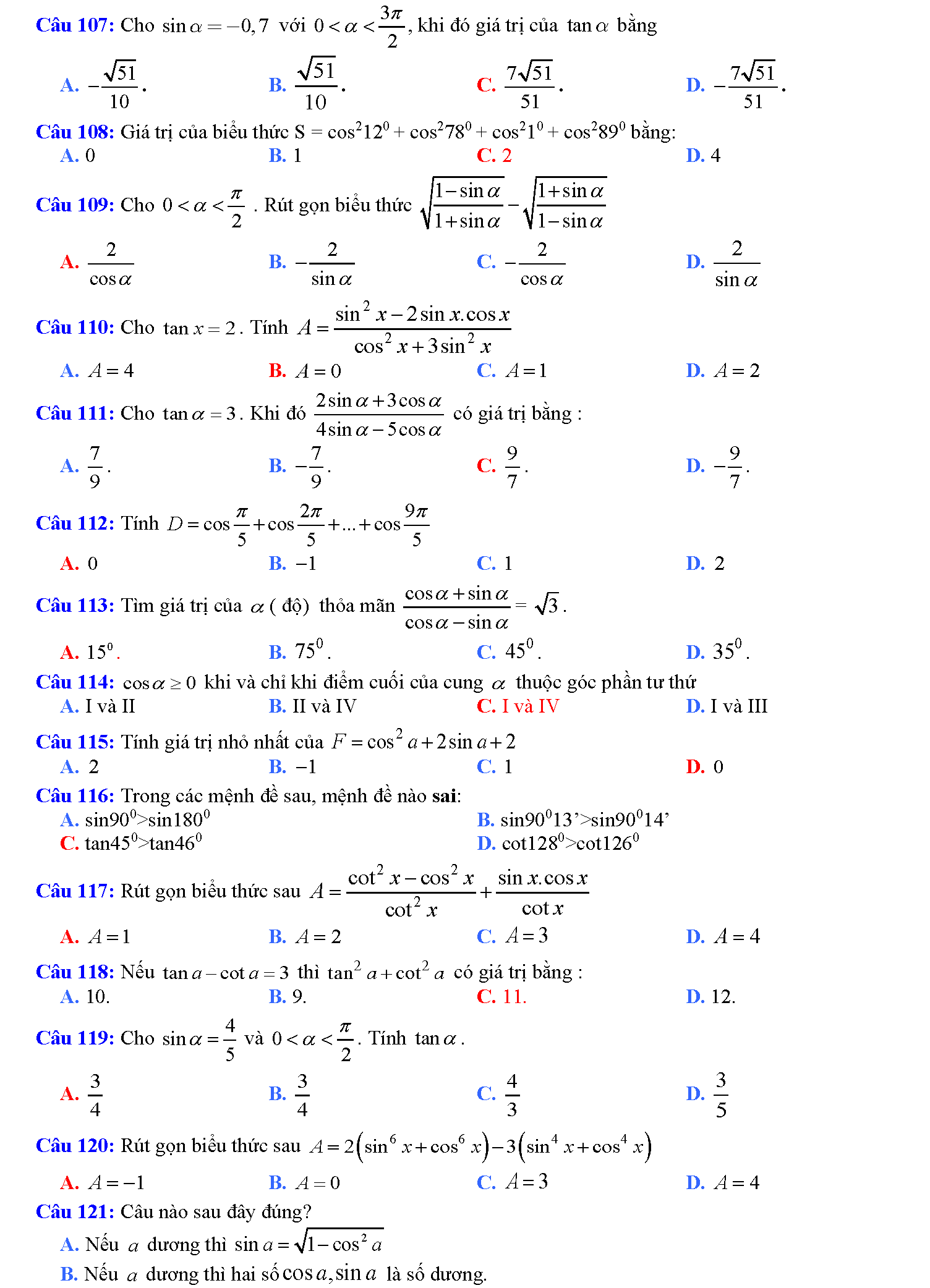
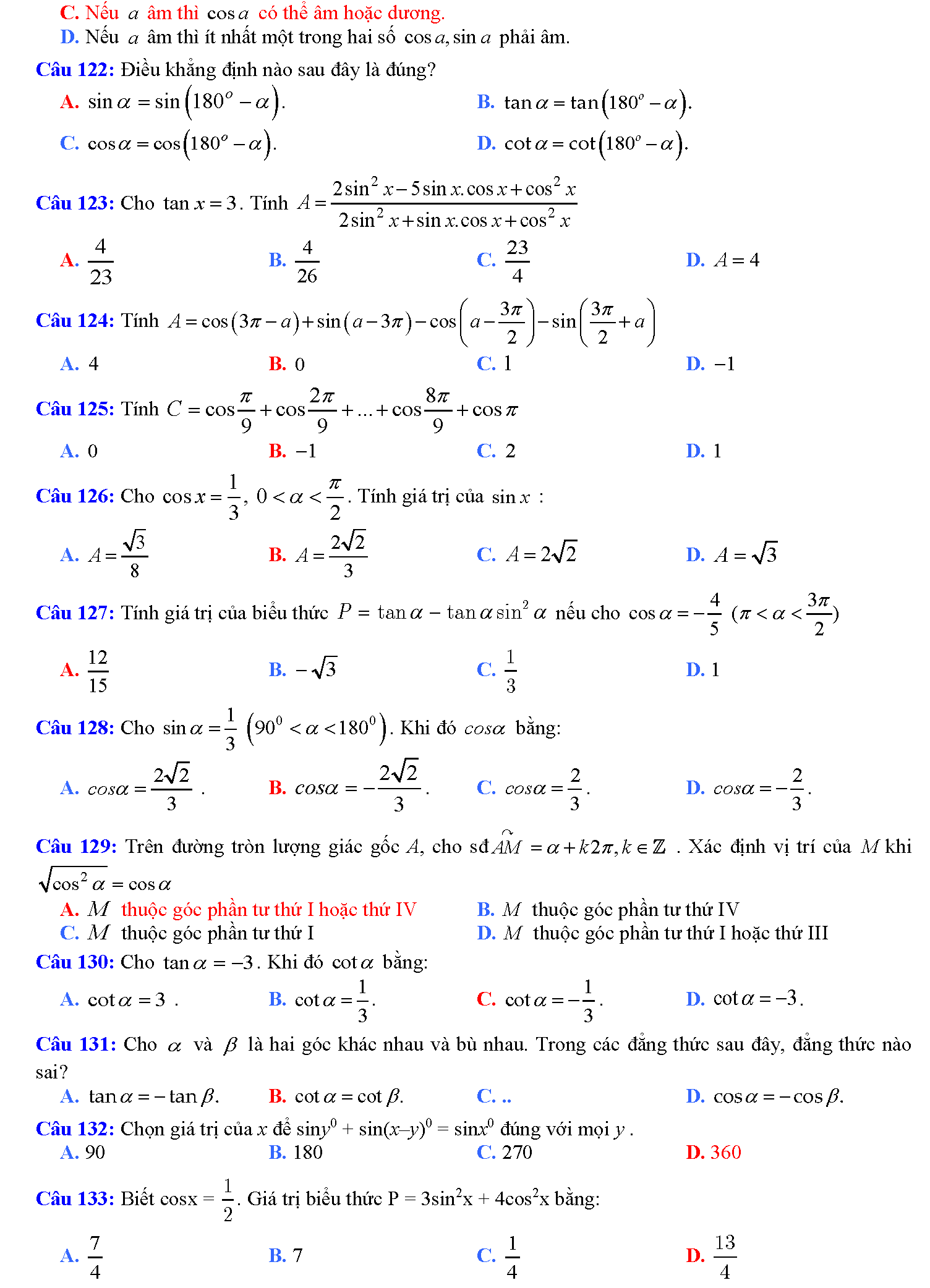
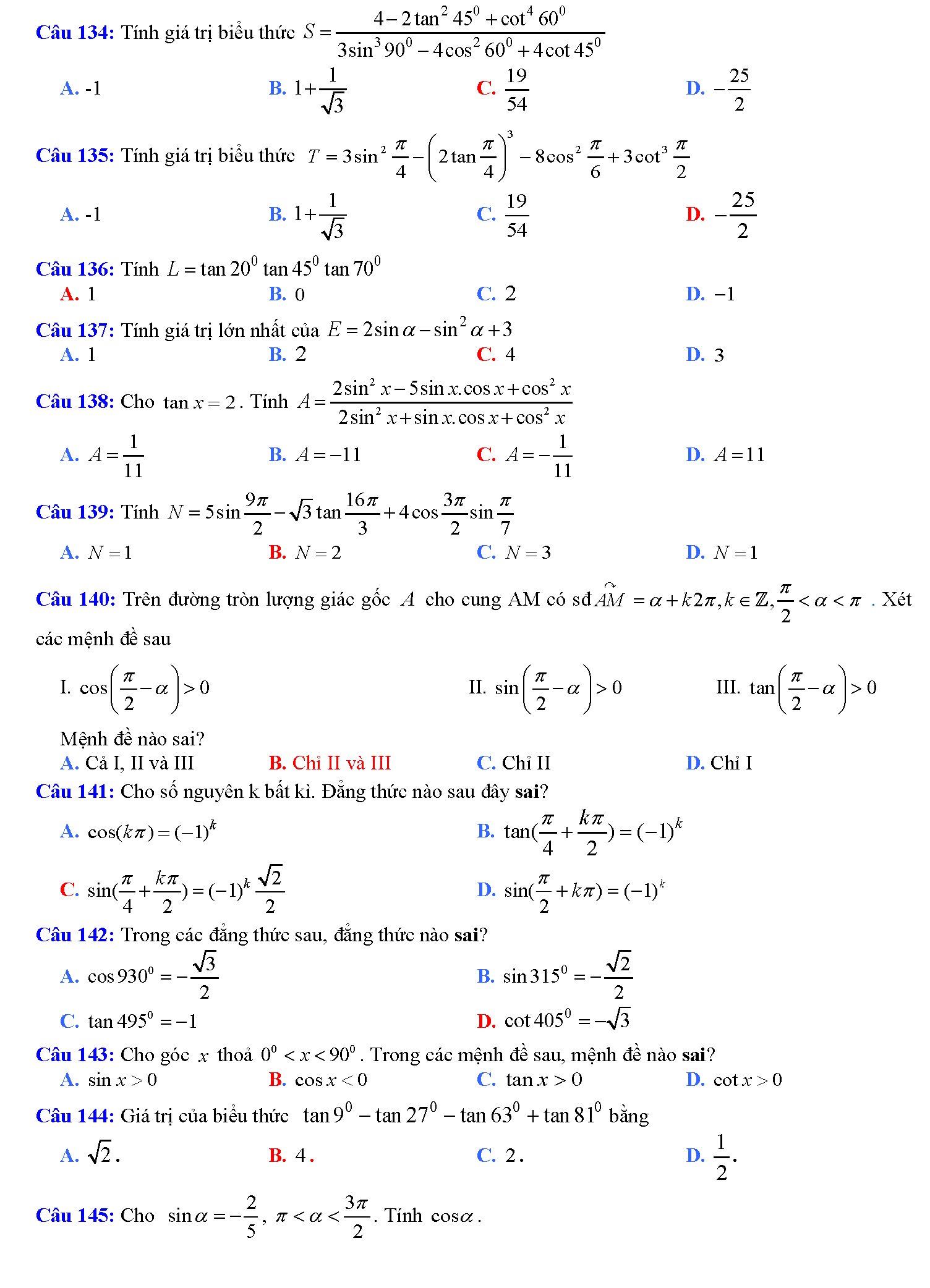
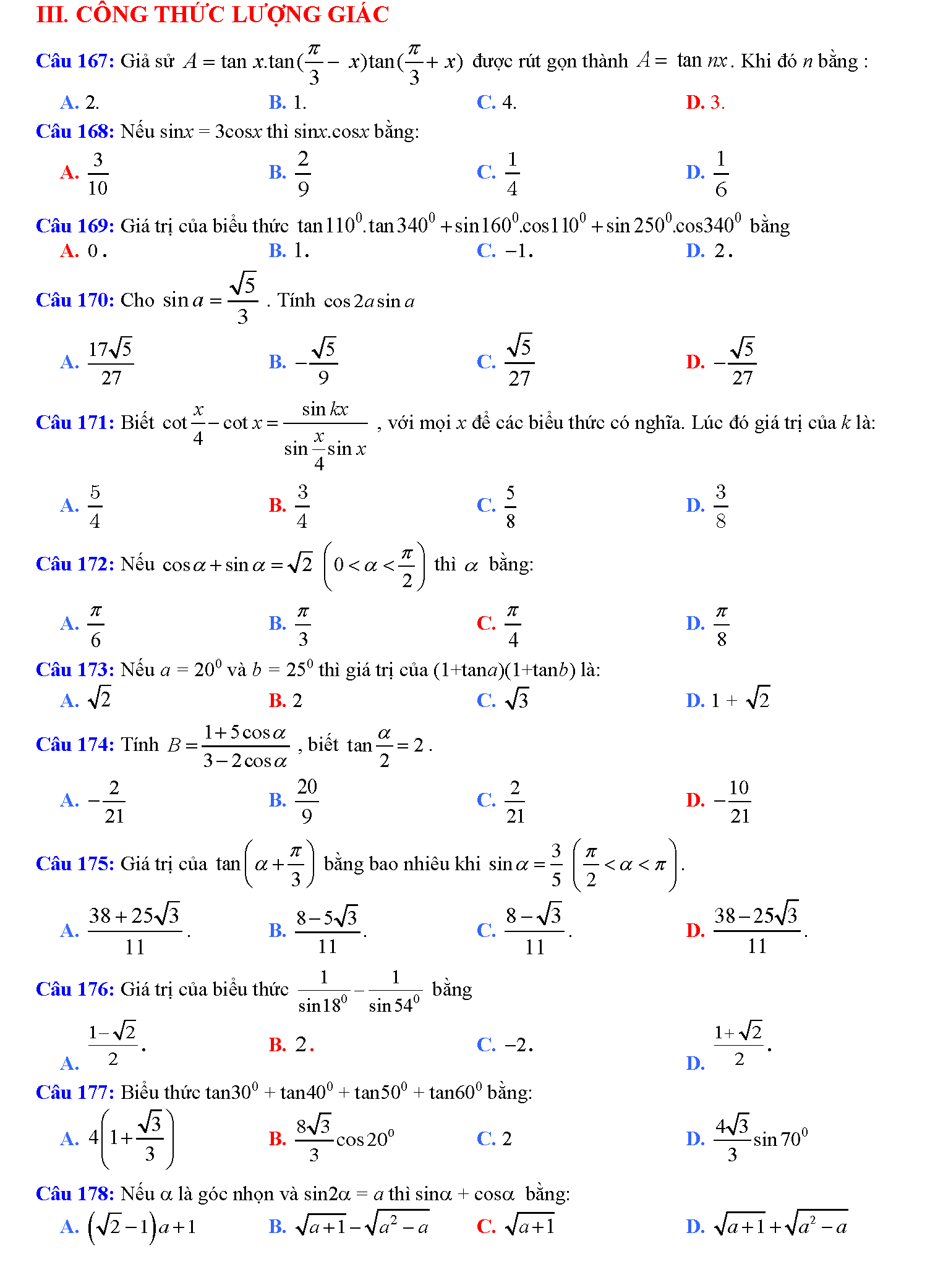
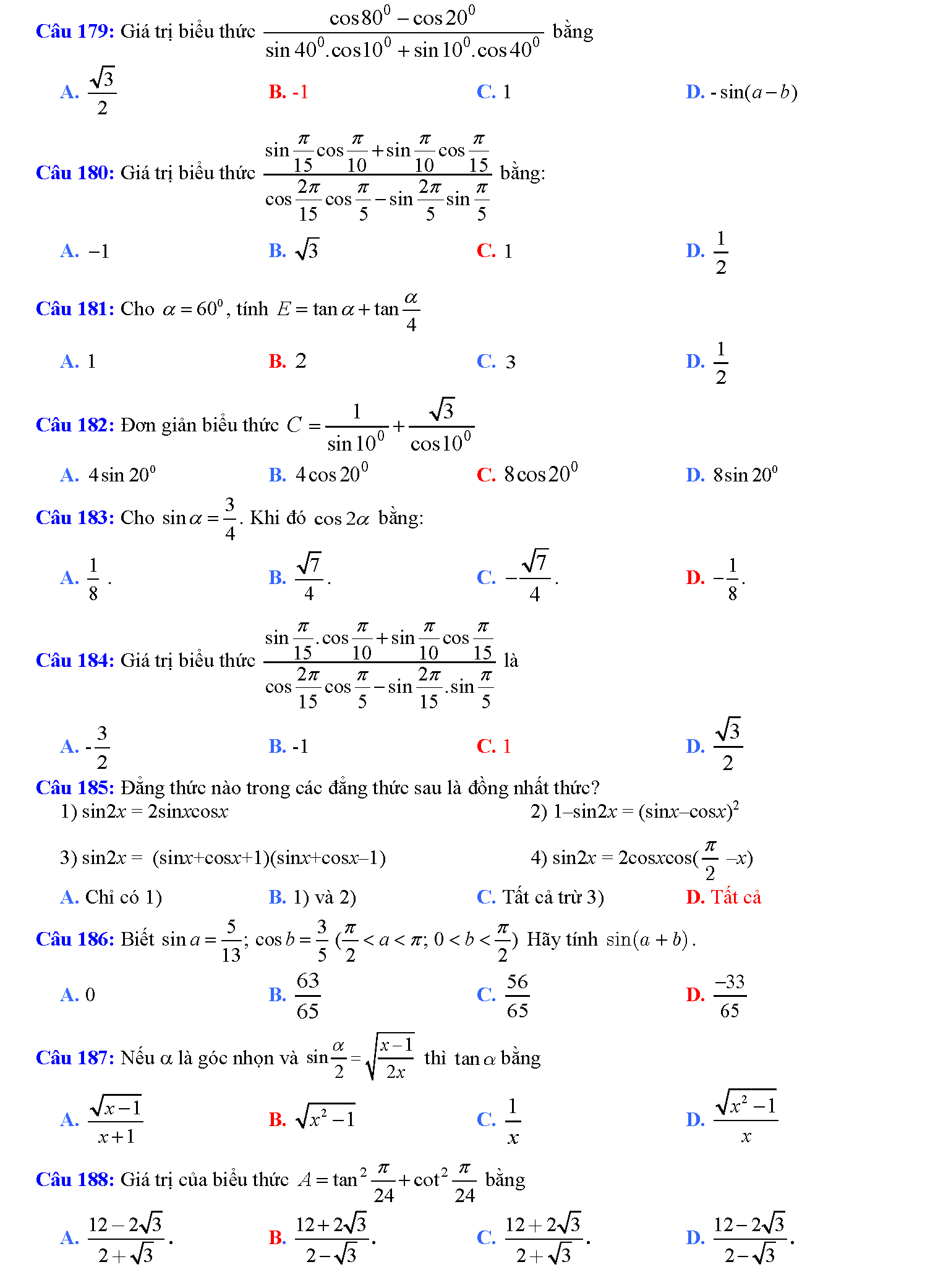
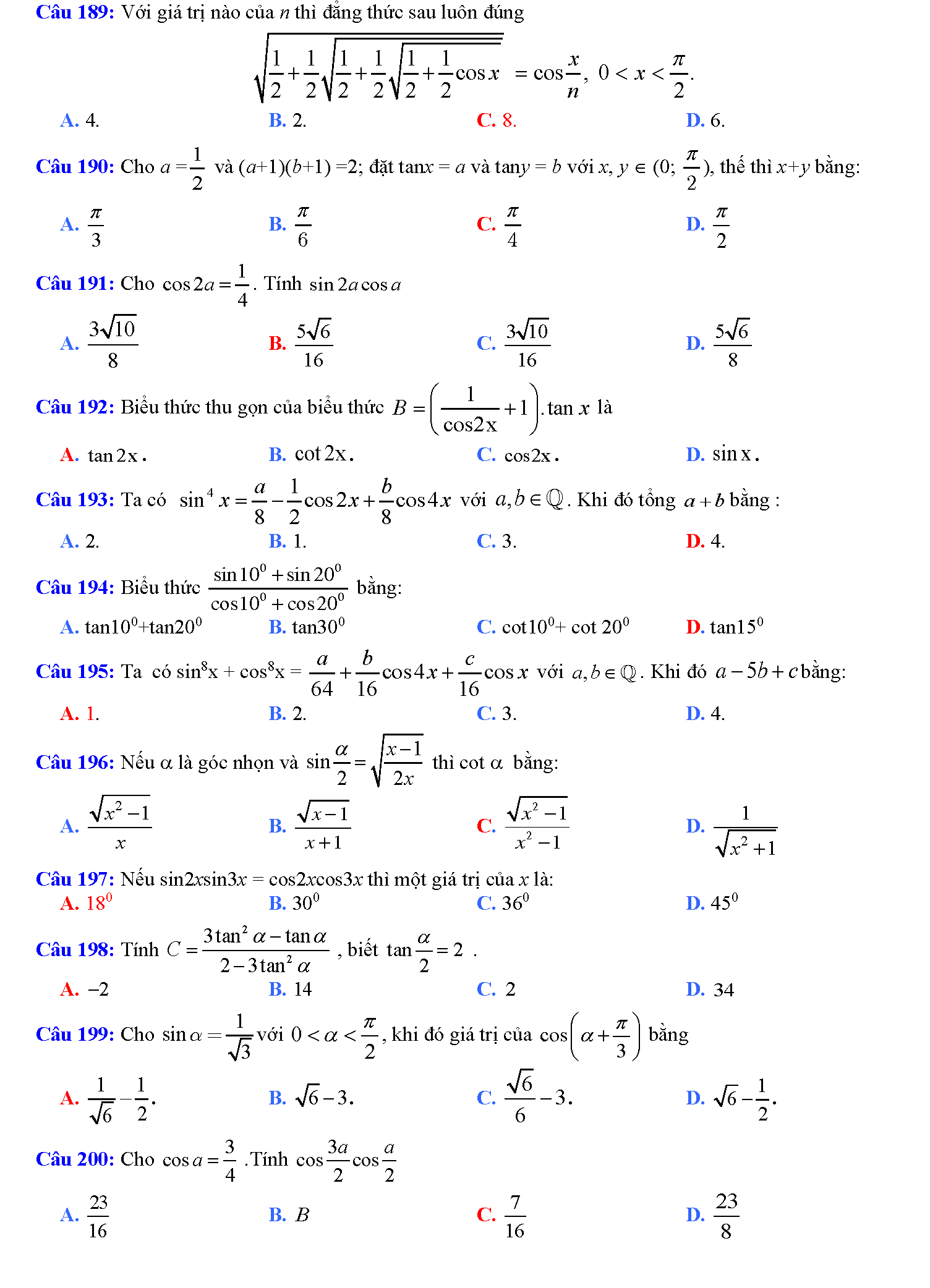
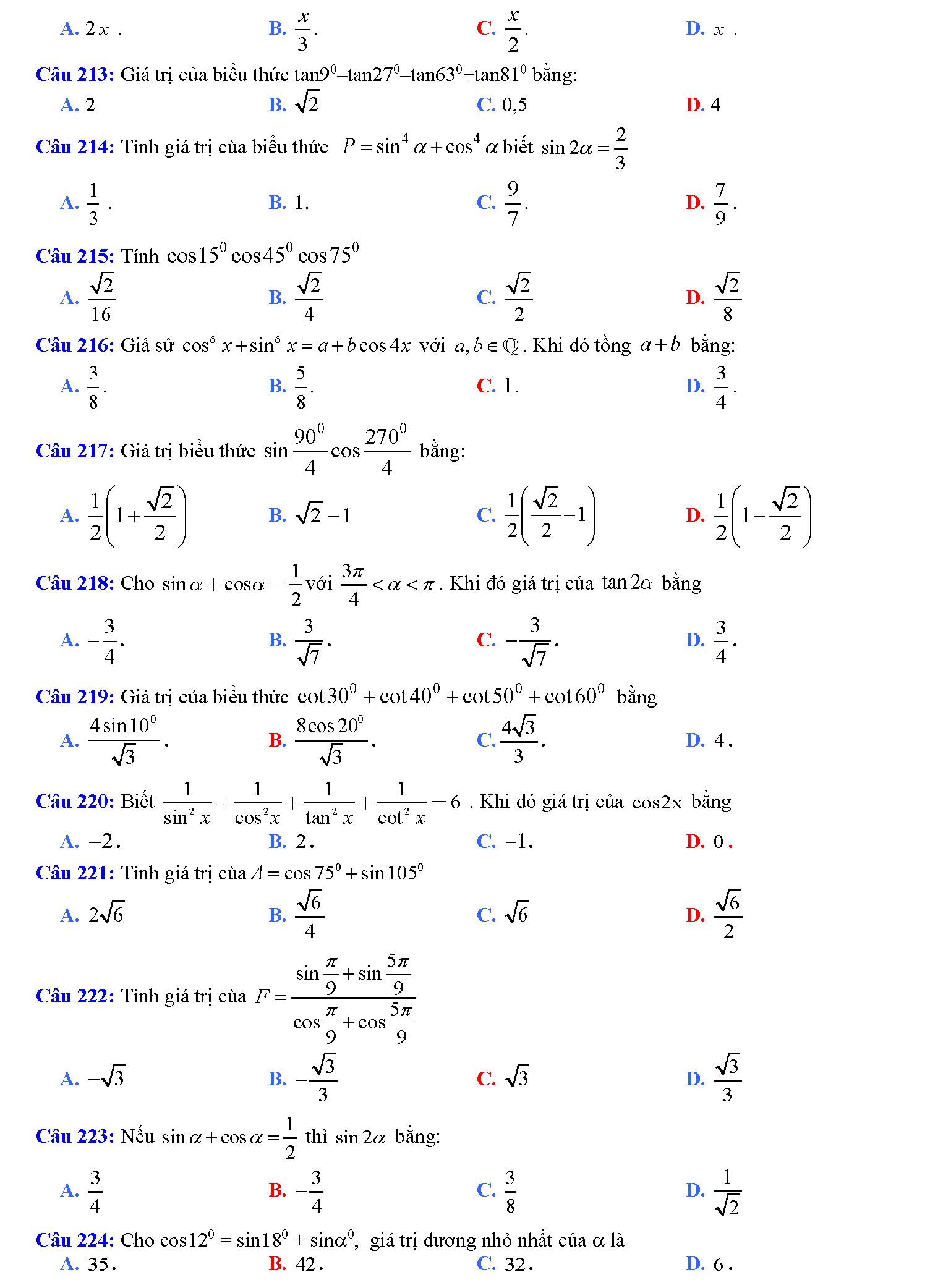
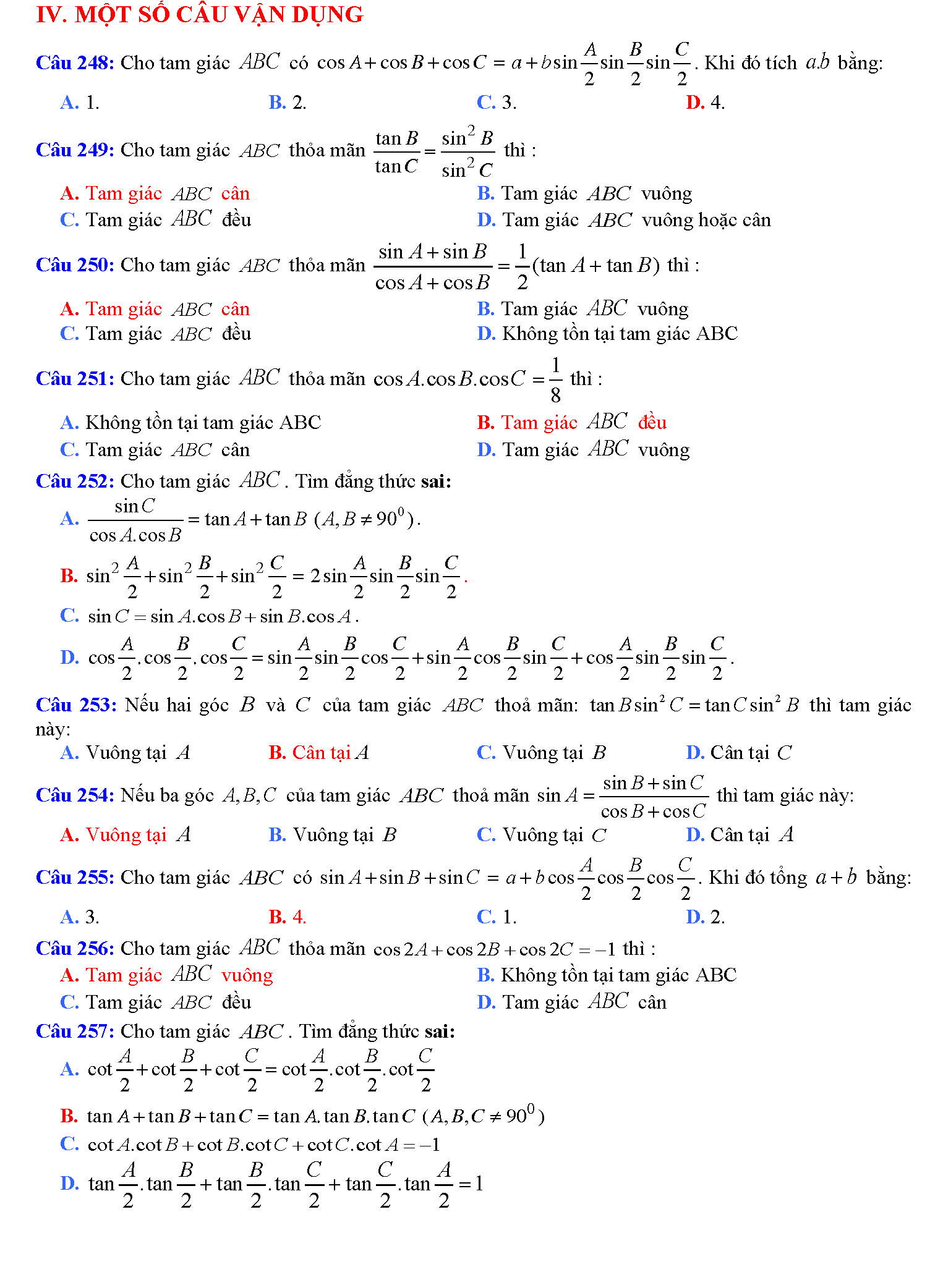
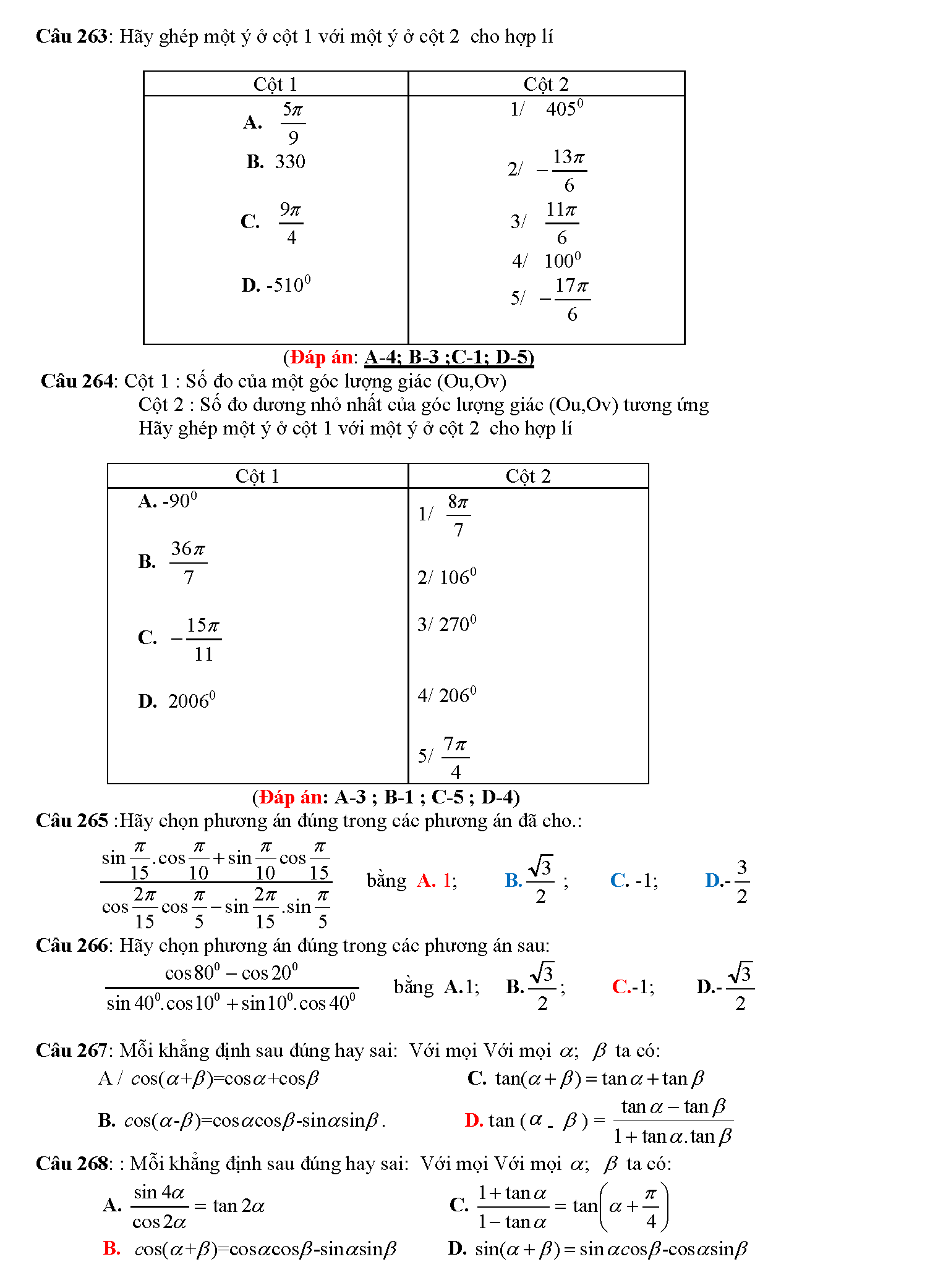
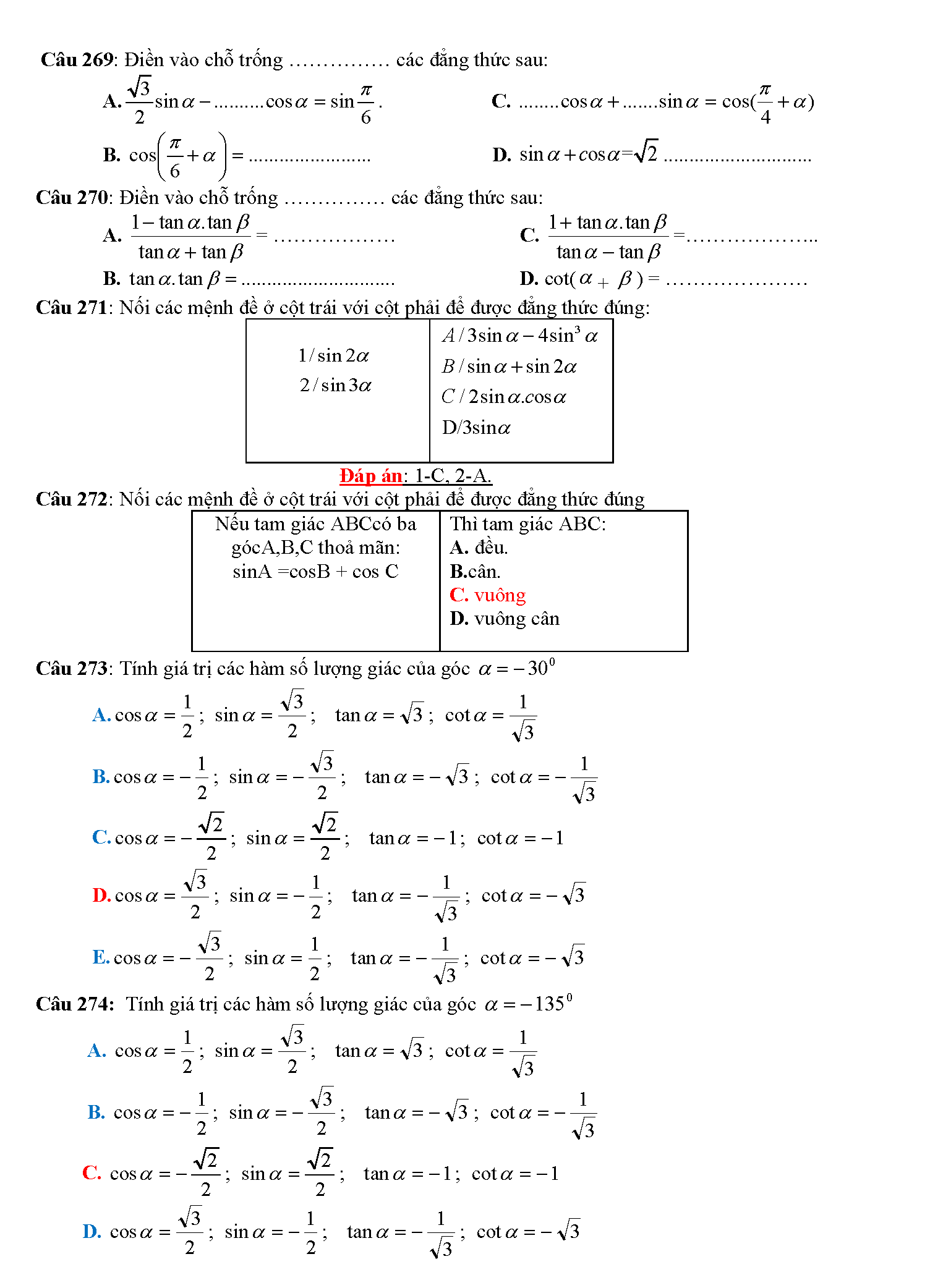
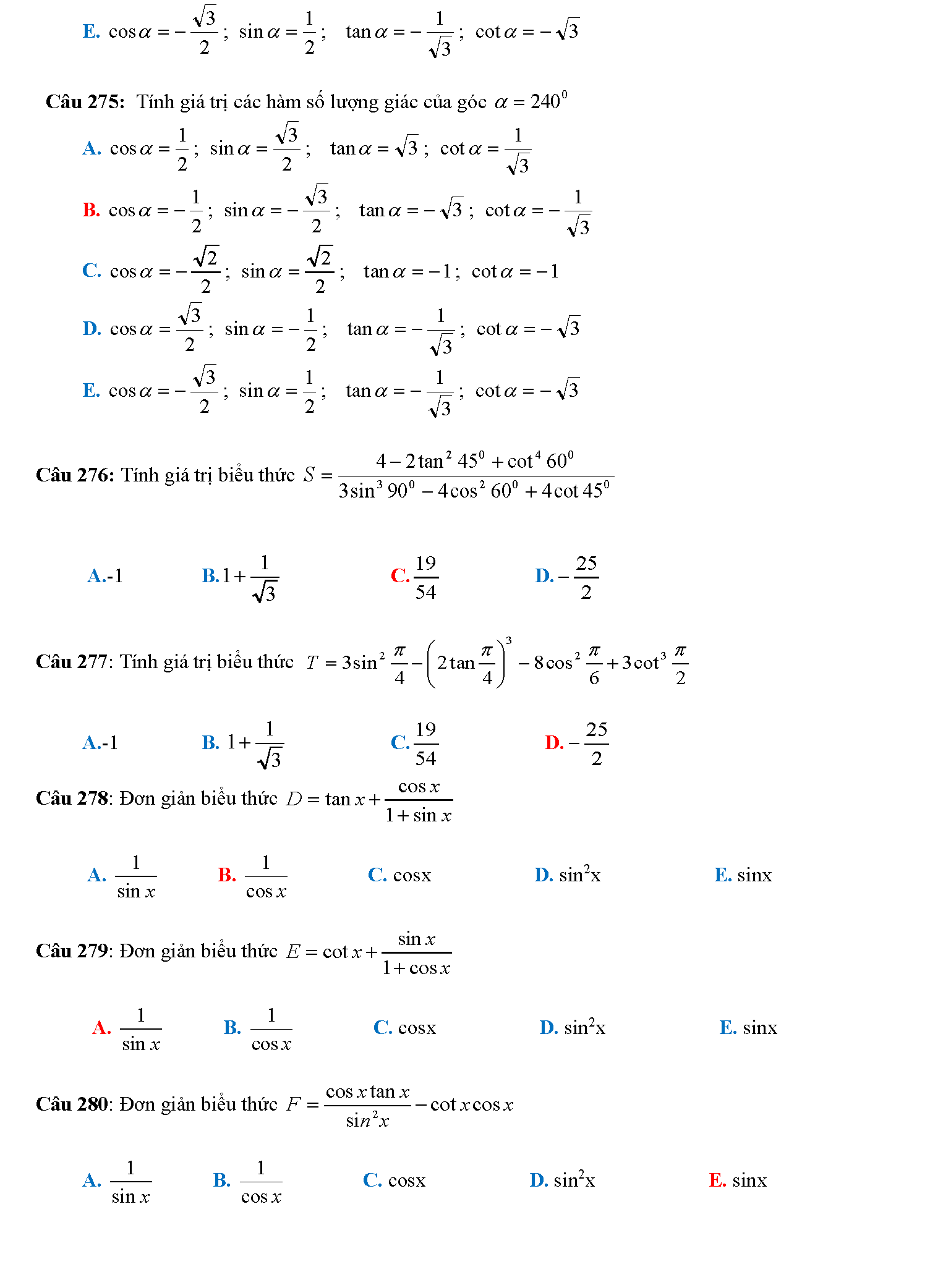
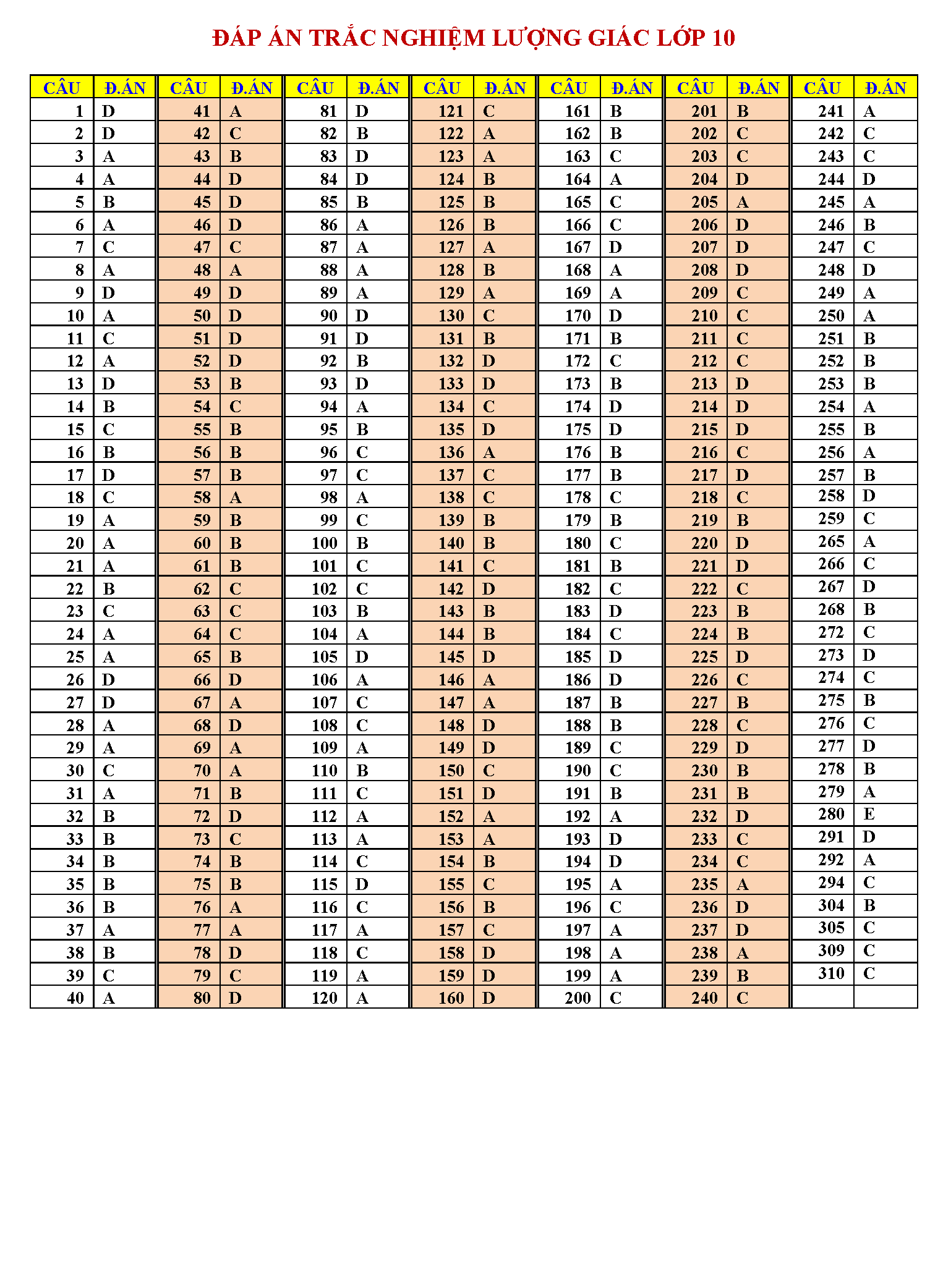
Vậy là chúng ta vừa tìm hiểu xong tất tần tật những công thức lượng giác hay nhất. Phải nói rằng, đây là bảng công thức lượng giác mà tailieure.com tâm huyết nhất từ trước đến giờ. Mong rằng với bảng này, các em học sinh sẽ không phải lo nghĩ gì khi gặp các bài toán lượng giác khó chịu. Bài viết còn có rất rất nhiều mẹo học lượng giác cực hay, do đó bạn nào có chứng hay quên giống admin thì cứ đọc thơ là sẽ thuộc mau nhớ dai nhé. Đừng quên ủng hộ website bằng cách ghé thăm lại nhiều lần. Tài liệu rẻ rất biết ơn nếu bạn chia sẽ những tài liệu này đến mọi người xung quanh. Lời cuối chúc các đọc giả thân mến học thật tốt.

Từ khóa của bài viết :

• bảng công thức lượng giác đầy đủ file word
• các công thức lượng giác nâng cao
• công thức lượng giác mở rộng
• công thức lượng giác lớp 9
• công thức lượng giác lớp 10 cần nhớ
• các công thức lượng giác lớp 10 nâng cao
• bảng lượng giác đặc biệt

Nguồn bài viết sưu tầm:

1 / https://www.facebook.com/notes/h%E1%BB%8Dc-v%C3%A0-h%C3%A0nh/nh%E1%BB%9B-c%C3%B4ng-th%E1%BB%A9c-l%C6%B0%E1%BB%A3ng-gi%C3%A1c-b%E1%BA%B1ng-nh%E1%BB%AFng-c%C3%A2u-th%C6%A1-%C4%91%C6%A1n-gi%E1%BA%A3n/361921053950747/
2 / http://khcb.tnus.edu.vn/chi-tiet/1242-GHI-NHO-CONG-THUC-LUONG-GIAC-BANG-THO

Source: http://wp.ftn61.com
Category: Thủ Thuật