✅ Cách giải nhanh đạo hàm ⭐️⭐️⭐️⭐️⭐

Đánh giá bài viết post

Cách tính nhanh đạo hàm của hàm số

Quy tắc tính đạo hàm các hàm số lượng giác lớp 11

Các hàm số u = u ( x ), v = v ( x ), w = w ( x ) có đạo hàm, khi đó .
( u + v ) ’ x = u ’ + v ’ ; ( u-v ) ’ = u ’ – v ’ ; ( ku ’ ) = k. u ’, k ∈ R .
( uv ) ’ = u’v + u. v ’ ; ( u / v ) ’ = ( u’v – uv ’ ) / v²
Đạo hàm những hàm số lượng giác lớp 11 .
( sinx ) ’ = cosx
( cosx ) ’ = – sinx
( tanx ) ’ = 1 / cos²x = 1 + tan²x ( x ≠ π / 2 + kπ, k ∈ Z ) .
( cotx ) ’ = – 1 / sin²x = – ( 1 + cot²x ) .
( x ≠ π, k ∈ Z ) .
( Sinu ) ’ = cosu. u ’ .
( cosu ) ’ = – sinu. u ’ .
( tanu ’ ) = u ’ / cos²u = ( 1 + tan²u ) u ’ ( u ≠ π / 2 + kπ, k ∈ Z ) .
( cotu ) ’ = – u ’ / sin²x = – 1 ( 1 + cot²u ) u ’ ( u ≠ kπ, k ∈ Z ) .
Trên đây là 1 số ít quy tắc tính đạo mà những em cần phải nhớ. Chỉ khi nắm vững được phần kiến thức và kỹ năng này những em mới hoàn toàn có thể thuận tiện giải được những bài toán xét tính đơn điêu, tìm giá trị lớn nhất, nhỏ nhất của hàm số lượng giác …

Bài tập tính đạo hàm các hàm số lượng giác lớp 11

Để hiểu và vận dụng linh động những quy tắc tính đạo hàm, những em hãy khám phá qua những ví dụ sau :
Ví dụ 1 :
Đạo hàm của hàm số y = 1 / ( cos²x – sin²x ) là :
A. y ’ = 2 sin2x / cos²2x B. y ’ = 2 cos2x / cos²2x
C. y ’ = cos2x / cos²2x D. y ’ = sin2x / cos²2x .
Hướng dẫn giải :
y = 1 / ( cos²x – sin²x ) = 1 / cos2x .

Áp dụng quy tắc tính đạo hàm với (1/u)’ = -u’/u² ta được”

y ’ = – ( cos2x ) ’ / ( cos2x ) ² = sin2x. ( 2 x ) ’ / cos²2x = 2 sin2x. cos²2x .
Ví dụ 2 : Cho hàm y = cotx / 2. Hệ thức nào sau đây là đúng ?
A. y² + 2 y ’ = 0 B. y² + 2 y ’ + 1 = 0
C. y² + 2 y ’ + 2 = 0 D. y² + 2 y ’ – 1 = 0 .
Đối với bài toán này, những em hoàn toàn có thể dùng 2 cách để giải :
Cách 1 :
Ta có y ’ = – 1 / ( sin²x / 2 ) = – 50% ( 1 + cot²x / 2 ) .
Do đó y² + 2 y ’ = cot²x / 2 – 2.1 / 2 ( 1 + cot²x / 2 ) = cot²x / 2 – ( 1 + cot²x / 2 ) = – 1 nên y² + 2 y ’ + 1 = 0. Chọn đáp án B .
Cách 2 : Sử dụng máy tính casio .
Bước 1 : Thiết lập môi trường tự nhiên SHIFT MODE 4 .
Thay x = 1 vào y = cotx / 2 ta tính được y cot 50% ≈ 1
Sử dụng phím SHIFT ∫, nhập hàm số y = cotx / 2 với x = 1 được hiệu quả ≈ – 1 .
Do đó y² + 2 y ’ + 1 = 0 .
Đối với những bài trắc nghiệm thì sử dụng máy tính cầm tay chính là tuyệt kỹ để những
Y ( n ) = ( – 1 ) ( n ) cos ( 2 x + n / 2 )
em rút ngắn thời hạn làm bài. Tuy nhiên cũng không nên vận dụng quá máy móc .

Đạo hàm của các hàm số lượng giác cấp cao

Ngoài những dạng bài tập trên, những em cũng cần chú đến bài toán tính đạo hàm cấp 2, cấp 3 của hàm số .
Ví dụ : Tính đạo hàm cấp n của hàm số y = cos2x là :
A. y ( n ) = ( – 1 ) ncos ( 2 x + n π / 2 )
B. y ( n ) = 2 n cos ( 2 x + π / 2 ) .
C. y ( n ) = 2 n + 1 cos ( 2 x + nπ / 2 ) .
D. y ( n ) = 2 n cos ( 2 x + nπ / 2 ) .
Ta có y ′ = 2 cos ( 2 x + π2 ), y ′ ′ = 2 ²cos ( 2 x + 2 π2 )
y ′ ′ ′ = 2 ³cos ( 2 x + 3 π2 )
Bằng quy nạp ta chứng tỏ được y ( n ) = 2 ncos ( 2 x + nπ2 )

Kĩ thuật Casio giải nhanh Giới Hạn, Đạo Hàm

Cách tính đạo hàm của hàm phân thức hữu tỉ

Để tính đạo hàm của hàm phân thức hữu tỉ thì những bạn sử dụng chung một công thức :

Tuy nhiên cũng có 1 số ít hàm phân thức tất cả chúng ta hoàn toàn có thể sử dụng những công thức tính đạo hàm nhanh .

Đạo hàm của hàm phân thức bậc 1/ bậc 1

Sử dụng công thức nhanh tính đạo hàm :

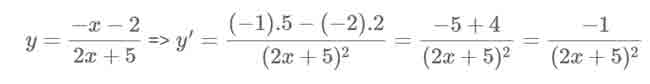
Xem thêm: Làm Thế Nào Để Học Giỏi Toán 8

Đạo hàm của hàm phân thức bậc 2/ bậc 1

Sử dụng công thức giải nhanh đạo hàm :

Đạo hàm của hàm phân thức bậc 2/ bậc 2

Một số trường hợp đặc biệt khi tính đạo hàm của hàm phân thức

Source: http://wp.ftn61.com
Category: Thủ Thuật