Cách tính diện tích tam giác nhanh và chuẩn nhất

Tính diện tích quy hoạnh tam giác là bài toán bạn hay gặp ở cấp tiểu học, với mỗi trường hợp đặc biệt quan trọng của tam giác có cách tính diện tích quy hoạnh khác nhau. Bài viết dưới đây hướng dẫn tới những bạn cách tính diện tích quy hoạnh của tam giác thường, vuông, cân và tam giác đều giúp bạn xử lý mọi bài toán bằng công thức hê rông và những công thức khác .

1. Công thức tính diện tích tam giác thường bằng công thức hê rông

Để tính diện tích quy hoạnh tam giác thường những bạn hoàn toàn có thể sử dụng những công thức sau :

1) ({S_{ABC}} = frac{1}{2}a.h)

Trong đó:

– a là độ dài 1 trong 3 cạnh của tam giác .
– h là độ dài đường cao tương ứng kẻ từ đỉnh đối lập với cạnh đáy có độ dài a .

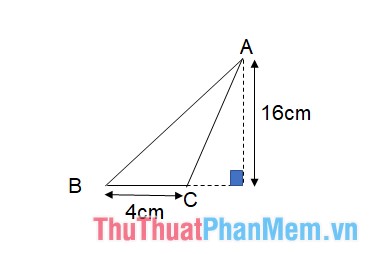
Ví dụ:  Tính diện tích tam giác ABC biết độ dài cạnh đáy BC = 4 cm, độ dài đường cao kẻ từ đỉnh A bằng 16 cm. Tính diện tích tam giác ABC.

Giải : Tam giác ABC có đường cao nằm ngoài tam giác. Diện tích tam giác vẫn được tính theo công thức : ( { S_ { ABC } } = frac { 1 } { 2 }. 4.16 = 32 left ( { c { m ^ 2 } } right ) )

2) ({S_{ABC}} = frac{1}{2}a.b.sin C = frac{1}{2}a.c.sin B = frac{1}{2}b.c.sin A)

Diện tích tam giác bằng 1 phần 2 tích 2 cạnh kề nhân với sin của góc hợp bởi 2 cạnh đó trong tam giác .

Ví dụ: Tính diện tích tam giác ABC biết AB = 8cm, BC = 6cm, góc B bằng 60 độ.

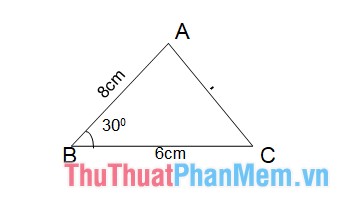
Giải : Theo công thức tính diện tích quy hoạnh tam giác ta có :
[{S_{ABC}} = frac{1}{2}a.b.sin C = frac{1}{2}.8.6.sin 30 = frac{1}{2}.48.frac{1}{2} = 12left( {c{m^2}} right)] [ { S_ { ABC } } = frac { 1 } { 2 } a.b.sin C = frac { 1 } { 2 }. 8.6.sin 30 = frac { 1 } { 2 }. 48.frac { 1 } { 2 } = 12 left ( { c { m ^ 2 } } right ) ]

3) Công thức Heron 

({S_{ABC}} = sqrt {p(p – a)(p – b)(p – c)} )

Công thức Hê rông – p là nửa chu vi của tam giác, a, b, c là độ dài của 3 cạnh trong tam giác
Ví dụ : Cho tam giác ABC với độ dài 3 cạnh : AB = 8 cm, BC = 6 cm, AC = 10 cm. Tính diện tích quy hoạnh tam giác ABC .

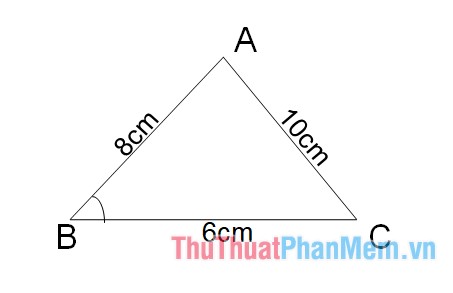
Giải
Ta có chu vi tam giác ABC là : ( { P_ { ABC } } = left ( { 8 + 6 + 10 } right ) = 24 ) cm
Vậy nửa chu vi tam giác bằng 12
Dựa theo công thức Hê rông tính diện tích quy hoạnh tam giác ABC là :
[ { S_ { ABC } } = sqrt { 12 left ( { 12 – 8 } right ) left ( { 12 – 6 } right ) left ( { 12 – 11 } right ) } = sqrt { 288 } approx 16,97 c { m ^ 2 } ]

4) ({S_{ABC}} = p.r)

(p là nửa chu vi của tam giác, r là bán kính đường tròn nội tiếp tam giác)

Ví dụ cho tam giác ABC biết chu vi tam giác bằng 28 cm. Biết nửa đường kính đường tròn ngoại tiếp tam giác bằng 3 cm. Tính diện tích quy hoạnh tam giác .

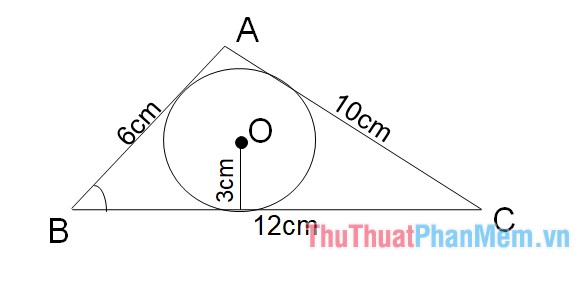
Giải
Nửa chu vi của tam giác bằng 28/2 = 14 cm
Diện tích tam giác ABC là : ( { S_ { ABC } } = p. r = 14.3 = 42 c { m ^ 2 } )

* Một số chú ý khi tính diện tích tam giác.

– Với tam giác có chứa góc bẹt chiều cao nằm bên ngoài tam giác .
– Khi tính diện tích quy hoạnh tam giác chiều cao nào ứng với đáy đó .
– Nếu hai tam giác có chung chiều cao hoặc chiều cao bằng nhau -> diện tích quy hoạnh hai tam giác tỉ lệ với 2 cạnh đáy và ngược lại nếu hai tam giác có chung đáy ( hoặc hai đáy bằng nhau ) -> diện tích quy hoạnh tam giác tỉ lệ với 2 đường cao tương ứng .

2. Công thức tính diện tích tam giác vuông

Công thức tính diện tích quy hoạnh tam giác vuông :

({S_{ABC}} = frac{1}{2}a.b) (với a, b là độ dài hai cạnh góc vuông)

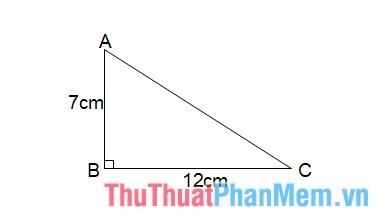
Ví dụ: Tam giác ABC vuông tại B, độ dài cạnh AB = 7 cm, cạnh BC = 12cm. Tính diện tích tam giác ABC.

Giải : Dựa vào công thức tính diện tích quy hoạnh tam giác vuông ta có :
[{S_{ABC}} = frac{1}{2}.AB.BC = frac{1}{2}.7.12 = 42left( {c{m^2}} right)] [ { S_ { ABC } } = frac { 1 } { 2 }. AB.BC = frac { 1 } { 2 }. 7.12 = 42 left ( { c { m ^ 2 } } right ) ]

3. Công thức tính diện tích tam giác cân

({S_{ABC}} = frac{1}{2}a.h) (Với a là độ dài cạnh đáy có thể là 1 trong 3 đáy, h là độ dài đường cao tương ứng kẻ tử đỉnh đối diện với cạnh đáy có độ dài a)

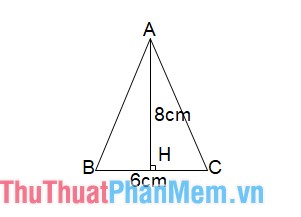
Ví dụ : Tam giác ABC cân tại A, đường cao AH có độ dài bằng 8 cm, cạnh đáy BC bằng 6 cm
=> Diện tích tam giác ABC :
[{S_{ABC}} = frac{1}{2}.8.6 = 24left( {c{m^2}} right)] [ { S_ { ABC } } = frac { 1 } { 2 }. 8.6 = 24 left ( { c { m ^ 2 } } right ) ]

4. Công thức tính diện tích tam giác đều

({S_{ABC}} = {a^2}.frac{{sqrt 3 }}{4}) (Với a là độ dài cạnh của tam giác)

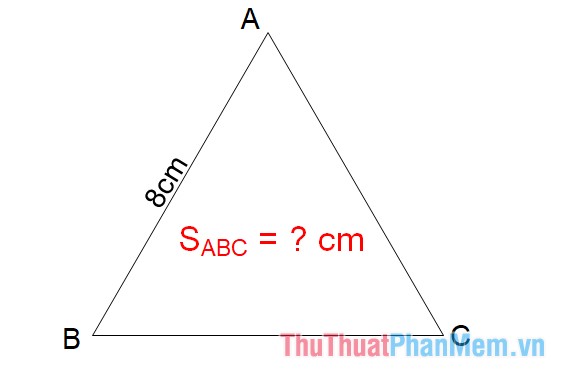
Ví dụ Tính diện tích quy hoạnh tam giác đều ABC biết độ dài cạnh AB = 8 cm .

Giải : Theo công thức tính diện tích quy hoạnh tam giác đều ta có :
[{S_{ABC}} = {a^2}.frac{{sqrt 3 }}{4} = {8^2}.frac{{sqrt 3 }}{4} = 16left( {c{m^2}} right)] [ { S_ { ABC } } = { a ^ 2 }. frac { { sqrt 3 } } { 4 } = { 8 ^ 2 }. frac { { sqrt 3 } } { 4 } = 16 left ( { c { m ^ 2 } } right ) ]Trên đây là công thức tính diện tích quy hoạnh tam giác Thường, Vuông, Cân, Đều giúp những bạn làm bài tập một cách thuận tiện. Chúc những bạn thành công xuất sắc .

Source: http://wp.ftn61.com
Category: Thủ Thuật