Cách tính diện tích đa giác chỉ vài giây suy nghĩ

Thẳng tiến vào ĐH chỉ với : Điểm lớp 12 Từ 6,5 – Điểm thi từ 18 năm 2021Bất cứ khi nào tất cả chúng ta nói về hình học, tất cả chúng ta nói về độ dài những cạnh, góc và diện tích của những hình dạng. Chúng ta đã thấy hai cái kia trước đây, hãy nói về cái sau. Bạn đã thấy rất nhiều câu hỏi trong kỳ thi toán học tương quan đến việc tìm diện tích vùng tô bóng của một đa giác đơn cử .
Vì vậy, bạn cần phải có kiến ​ ​ thức về công thức diện tích của những loại đa giác .

Trong bài viết này, bạn sẽ học:

• Diện tích của một đa giác có nghĩa là gì?
• Làm thế nào để tìm diện tích của một đa giác, bao gồm cả diện tích của đa giác đều và bất thường?

Diện tích của một đa giác là gì?

Trong hình học, diện tích được định nghĩa là vùng chiếm bên trong ranh giới của một hình hai chiều. Do đó, diện tích của một đa giác là tổng không gian hoặc vùng giới hạn bởi các cạnh của đa giác.

QUẢNG CÁO
Đơn vị tiêu chuẩn để đo diện tích là mét vuông ( m 2 ) .

Làm thế nào để Tìm diện tích của một đa giác?

Các đa giác thông thường như hình chữ nhật, hình vuông, hình thang, hình bình hành, v.v. có các công thức xác định trước để tính diện tích của chúng.

Tuy nhiên, đối với một đa giác không đều , diện tích được tính bằng cách chia một đa giác không đều thành các phần nhỏ của đa giác đều.

Diện tích của một đa giác đều

Tính diện tích của một đa giác đều hoàn toàn có thể đơn thuần như tìm diện tích của một tam giác đều. Đa giác đều có độ dài những cạnh bằng nhau và số đo những góc bằng nhau .

Có ba phương pháp tính diện tích của một đa giác đều . Mỗi phương pháp được sử dụng trong những dịp khác nhau.

Diện tích của một đa giác bằng cách sử dụng khái niệm apothem

Diện tích của một đa giác đều hoàn toàn có thể được tính bằng cách sử dụng khái niệm apothem. Apothem là một đoạn thẳng nối tâm của đa giác với trung điểm của bất kể cạnh nào vuông góc với cạnh đó. Do đó, diện tích của một đa giác đều được cho bởi ;
A = 50%. p. a
trong đó p = chu vi của đa giác = tổng toàn bộ độ dài những cạnh của đa giác .
a = apothem .
Hãy xem xét một ngũ giác được hiển thị dưới đây ;

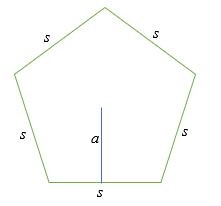
Nếu apothem, a = x và độ dài mỗi cạnh của ngũ giác là s, thì diện tích của ngũ giác được cho bởi ;

Diện tích = 1/2. p. a

Chu vi = s + s + s + s + s
= 5 giây
Vì vậy, sửa chữa thay thế ,
Diện tích = ( ½ ) 5 sx
= ( 5/2 ) ( s. X ) Sq. những đơn vị chức năng
Khi sử dụng giải pháp apothem, độ dài của apothem sẽ luôn được cung ứng .

Diện tích của một đa giác theo công thức: A = (L 2 n) / [4 tan (180 / n)]

Ngoài ra, hoàn toàn có thể tính diện tích của đa giác bằng công thức sau ;
A = ( L 2 n ) / [ 4 tan ( 180 / n ) ] Trong đó, A = diện tích của đa giác ,
L = Chiều dài của cạnh
n = Số cạnh của đa giác đã cho .

Diện tích của một đa giác ngoại tiếp

Diện tích của một đa giác nội tiếp một đường tròn được cho bởi ,

A = [n / 2 × L × √ (R² – L² / 4)] đơn vị hình vuông.

Trong đó, n = số cạnh .
L = Độ dài cạnh của một đa giác
R = Bán kính của đường tròn ngoại tiếp .
Hãy giải một vài bài toán ví dụ về diện tích của một đa giác đều .

ví dụ 1

Tìm diện tích của một hình lục giác đều có những cạnh là 6 m .
Giải pháp
Đối với một hình lục giác, số cạnh, n = 6
L = 6 m
A = ( L 2 n ) / [ 4 tan ( 180 / n ) ] Bằng cách thay thế sửa chữa ,
A = ( 6 2 6 ) / [ 4 tan ( 180 / 6 ) ] = ( 36 * 6 ) / [ 4 tan ( 180 / 6 ) ] = 216 / [ 4 tan ( 180 / 6 ) ] = 216 / 2.3094
A = 93,53 m 2

Ví dụ 2

Tìm diện tích của một hình lục giác đều có cạnh là 10√3 cm và độ dài cạnh là 20 cm.

Giải pháp

Diện tích = ½ pa

Đầu tiên, tìm chu vi của hình lục giác .
p = ( 20 + 20 + 20 + 20 + 20 + 20 ) cm = ( 20 cm * 6 )
= 120 cm
Người thay thế sửa chữa .

Diện tích = ½ pa

= ½ * 120 * 10 √ 3
= 600 √ 3 cm 2

Ví dụ 3

Tìm diện tích của một ngũ giác đều, nếu chiều dài của đa giác là 8 m và bán kính của đường tròn ngoại tiếp là 7 m.
Lời giải
A = [n / 2 × L × √ (R² – L² / 4)] đơn vị bình phương.

Trong đó, n = 5 ; L = 8 m và R = 7 m .
Bằng cách sửa chữa thay thế ,
A = [ 5/2 × 8 × √ ( 7 ² – 8 ² / 4 ) ] m 2
= [ 20 √ ( 49 – 64/4 ) ] = 20 √ ( 49 – 16 )
= 20 √ 33 m 2
= 20 * 5,745 m 2
= 114,89 m 2

Ví dụ 4

Tìm diện tích của một hình ngũ giác đều có cạnh và cạnh dài lần lượt là 15 cm và 18 cm .
Giải pháp
Diện tích = ½ pa
a = 15 cm
p = ( 18 * 5 ) = 90 cm
A = ( ½ * 90 * 15 ) cm
= 675 cm .

Diện tích đa giác không đều

Đa giác không đều là một đa giác có những góc bên trong có độ đo khác nhau. Độ dài những cạnh của một đa giác không đều cũng có những số đo khác nhau .
Như đã nói ở trên, diện tích của một đa giác không đều hoàn toàn có thể được tính bằng cách chia một đa giác không đều thành những phần nhỏ của đa giác đều .

Xem thêm:

Làm thế nào để tìm các góc của một đa giác nhanh chóng nhất

Đa giác – Giải thích & Ví dụ chưa bao giờ đơn giản đến thế!

Ví dụ 5

Tìm diện tích của một đa giác không đều dưới đây nếu AB = ED = 20 cm, BC = CD = 5 cm và AB = BD = 8 cm

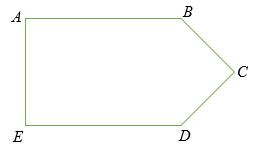
Giải pháp
Chia đa giác không đều thành những phần của đa giác đều

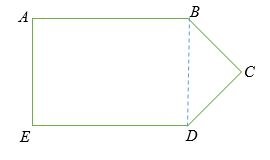
Do đó, ABED là hình chữ nhật và BDC là hình tam giác .
Diện tích hình chữ nhật = l * w
= 20 * 8 = 160 cm 2
Diện tích tam giác = 50%. b. h
Chiều cao của tam giác hoàn toàn có thể được tính bằng cách vận dụng định lý Pythagoras. Ví dụ ,
c 2 = a 2 + b 2
25 2 = a 2 + 4 2
a = √ ( 25 – 16 )
a = 3
A = ½bh = ½ * 3 * 8

= 6 cm 2

Bây giờ thêm những khu vực một phần .
Diện tích đa giác = ( 160 + 6 ) cm 2 = 166 cm 2

Source: http://wp.ftn61.com
Category: Thủ Thuật