Lý thuyết và phương pháp giải bài toán từ thông và suất điện động xoay chiều

Cập nhật lúc : 16 : 27 17-06-2015 Mục tin : Vật lý lớp 12

Bài viết trình bày lý thuyết và phương pháp giải bài tập từ thông và suất điện động xoay chiều rất chi tiết và cụ thể. Một số ví dụ có lời giải chi tiế giúp bạn nắm trắc kiến thức hơn.

LÝ THUYẾT VÀ PHƯƠNG PHÁP GIẢI BÀI TOÁN TỪ THÔNG VÀ SUẤT ĐIỆN ĐỘNG XOAY CHIỀU

I.Cách tạo ra suất điện động xoay chiều:

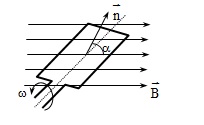
Cho khung dây dẫn phẳng có N vòng, diện tích quy hoạnh Squay đều với tốc độ ω, xung quanh trục vuông góc với với những đường sức từcủa một từ trường đều có cảm ứng từ \ ( \ overrightarrow { B } \ ). Theo định luật cảm ứng điện từ, trongkhung dây Open một suất điện động biến hóa theo định luật dạng cosin vớithời hạn gọi tắt là suất điện động xoay chiều :\ ( e = E_ { 0 } cos ( \ omega t + \ varphi _ { 0 } ) \ )

1.Từ thông gởi qua khung dây :

– Từ thông gửi qua khung dây dẫn gồm N vòng dây có diện tích quy hoạnh S quay trong từ trường đều \ ( \ overrightarrow { B } \ ). Giả sử tại t = 0 thì : \ ( ( \ vec { n }, \ vec { B } ) = \ varphi \ )=> Biểu thức từ thông của khung : \ ( \ Phi = N.B.S.cos \ omega t = \ Phi _ { 0 }. cos \ omega t \ )( Với \ ( \ Phi = LI \ ) và Hệ số tự cảm L = 4 π. 10-7 N2. S / l )- Từ trải qua khung dây cực lớn \ ( \ Phi = NBS \ ) ; ω là tần số góc bằng vận tốc quay của khung ( rad / s )Đơn vị : + Φ : Vêbe ( Wb ) ;+ S : Là diện tích quy hoạnh một vòng dây ( S : mét vuông ) ;+ N : Số vòng dây của khung+ \ ( \ overrightarrow { B } \ ) : Véc tơ cảm ứng từ của từ trường đều. B : Tesla ( T )( \ ( \ overrightarrow { B } \ ) vuông góc với trục quay ∆ )+ ω : Vận tốc góc không đổi của khung dây( Chọn gốc thời hạn t = 0 lúc \ ( ( \ vec { n }, \ vec { B } ) = 0 ^ { 0 } \ )- Chu kì và tần số của khung : \ ( T = \ frac { 2 \ pi } { \ omega } ; f = \ frac { 1 } { T } \ )

   2. Suất điện động xoay chiều:

– Biểu thức của suất điện động cảm ứng tức thời :

\(e=\frac{-\Delta \Phi }{\Delta t}=-\Phi ‘=\omega NBS.sin\omega\)\(t=E_{o}cos(\omega t-\frac{\pi }{2})\)  

\ ( e = E_ { o } cos ( \ omega t + \ varphi _ { 0 } ) \ ) Đặt \ ( E_ { 0 } = NB \ omega S \ ) : Suất điện động cực lớn\ ( \ varphi _ { 0 } = \ varphi – \ frac { \ pi } { 2 } \ )Đơn vị : e, E0 ( V )

.Phương pháp:

Thông thường bài tập thuộc dạng này yêu cầu ta tính từ thông, suất điện động cảm ứng xuất hiện trong

khung dây quay trong từ trường. Ta sử dụng các công thức sau để giải:

– Tần số góc: \(\omega =2\pi n_{0}\), Với n0 là số vòng quay trong mỗi giây bằng tần số dòng điện xoay chiều.

– Biểu thức từ thông: \(\Phi =\Phi _{0}cos(\omega t+\varphi )\)  ,  Với    \(\Phi _{0}\)= NBS.

– Biểu thức suất điện động: \(e=E _{0}sin(\omega t+\varphi )\)  Với Eo = NBSω ; \(\varphi =(\vec{B},\vec{n})\)   lúc t=0.

– Vẽ đồ thị: Đồ thị là đường hình sin:   * có chu kì :  \(T=\frac{2\pi }{\omega }\)      * có biên độ: \(E_{0}\)

2.Bài tập áp dụng :

Bài  1 : Một khung dây dẫn phẳng có diện tích S = 50 cm2, có N = 100 vòng dây, quay đều với tốc độ 50 vòng/giây quanh một trục vuông góc với các đường sức của một từ trường đều có cảm ứng từ B = 0,1 T. Chọn gốc thời gian t = 0 là lúc vectơ pháp tuyến \(\vec{n}\) của diện tích S của khung dây cùng chiều với vectơ cảm ứng từ  \(\overrightarrow{B}\) và chiều dương là chiều quay của khung dây.

a ) Viết biểu thức xác lập từ thông Φ qua khung dây .b ) Viết biểu thức xác lập suất điện động e Open trong khung dây .c ) Vẽ đồ thị trình diễn sự biến hóa của e theo thời hạn .

Bài  giải :

a ) Khung dây dẫn quay đều với vận tốc góc : ω = 50.2 π = 100 π rad / sTại thời gian khởi đầu t = 0, vectơ pháp tuyến \ ( \ vec { n } \ ) của diện tích quy hoạnh S của khung dây có chiều trùng với chiều của vectơ cảm ứng từ \ ( \ overrightarrow { B } \ ) của từ trường. Đến thời gian t, pháp tuyến \ ( \ vec { n } \ ) của khung dây đã quay được một góc bằng ωt. Lúc này từ trải qua khung dây là :\ ( \ Phi = NBS \ ) cos ( ωt )Như vậy, từ trải qua khung dây biến thiên điều hoà theo thời hạn với tần số góc ω và với giá trị cực lớn ( biên độ ) là Ф0 = NBS .Thay N = 100, B = 0,1 T, S = 50 cm2 = 50. 10-4 mét vuông và ω = 100 π rad / s ta được biểu thức của từ trải qua khung dây là : \ ( \ Phi = 0,05 cos ( 100 \ pi t ) \ ) ( Wb )b ) Từ trải qua khung dây biến thiên điều hoà theo thời hạn, theo định luật cảm ứng điện từ của Faraday thì trong khung dây Open một suất điện động cảm ứng .

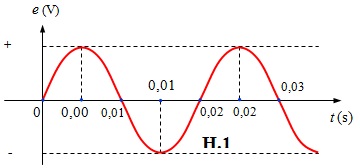
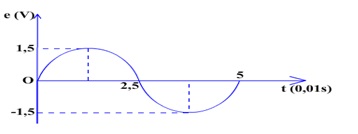
Suất điện động cảm ứng Open trong khung dây được xác lập theo định luật Lentz :\ ( e = – \ frac { d \ Phi } { dt } = – \ Phi ‘ _ { t } = \ omega NBSsin ( \ omega t ) = \ omega NBScos ( \ omega t – \ frac { \ pi } { 2 } ) \ )Như vậy, suất điện động cảm ứng Open trong khung dây biến hóa điều hoà theo thời hạn với tần số góc ω và với giá trị cực lớn ( biên độ ) là E0 = ωNBS .Thay N = 100, B = 0,1 T, S = 50 cm2 = 50. 10-4 mét vuông và ω = 100 π rad / s ta được biểu thức xác lập suất điện động Open trong khung dây là :\ ( e = 5 \ pi cos ( 100 \ pi t – \ frac { \ pi } { 2 } ) \ ) ( V ) hay \ ( e \ approx 15,7 cos ( 314 t – \ frac { \ pi } { 2 } ) \ ) ( V )c ) Suất điện động Open trong khung dây đổi khác điều hoà theo thời hạn với chu khì T và tần số f lần lượt là :\ ( T = \ frac { 2 \ pi } { \ omega } = \ frac { 2 \ pi } { 100 \ pi } = 0,02 s ; f = \ frac { 1 } { T } = \ frac { 1 } { 0,02 } = 50H z \ )Đồ thị trình diễn sự biến hóa của suất điện động e theo thời hạn t là đường hình sin có chu kì tuần hoàn T = 0,02 s. Bảng giá trị của suất điện động e tại 1 số ít thời gian đặc biệt quan trọng như : 0 s, \ ( \ frac { T } { 4 } = 0,005 s ; \ frac { T } { 2 } = 0,01 s, \ frac { 3T } { 4 } = 0,015 s, T = 0,02 s, \ frac { 5T } { 4 } = 0,025 s \ ) và \ ( \ frac { 3T } { 2 } = 0,03 s \ ) :

t ( s )
0
0,005
0,01
0,015
0,02
0,025
0,03
e ( V )
0

15,7

0
– 15,7
0
15,7
0
Đồ thị trình diễn sự nhờ vào của e theo t như hình trên H1 :

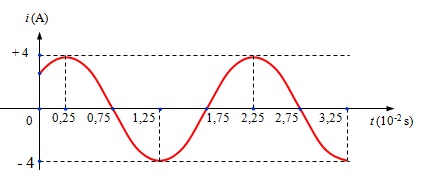
Bài  2 : Dòng điện xoay chiều chạy qua một đoạn mạch có cường độ biến đổi điều hoà theo thời gian được mô tả bằng đồ thị ở hình dưới đây.

a ) Xác định biên độ, chu kì và tần số của dòng điện .b ) Đồ thị cắt trục tung ( trục Oi ) tại điểm có toạ độ bao nhiêu ?

Bài  giải :

a ) Biên độ chính là giá trị cực lớn I0 của cường độ dòng điện. Dựa vào đồ thị ta có biên độ của dòng điện này là : I0 = 4 A .Tại thời gian 2,5. 10-2 s, dòng điện có cường độ tức thời bằng 4 A. Thời điểm tiếp nối mà dòng điện có cường độ tức thời bằng 4 A là 2,25. 10-2 s. Do đó chu kì của dòng điện này là :T = 2,25. 10-2 – 0,25. 10-2 = 2.10 – 2 s ; Tần số của dòng điện này là : \ ( f = \ frac { 1 } { T } = \ frac { 1 } { 2.10 ^ { – 2 } } = 50H z \ )b ) Biểu thức cường độ dòng điện xoay chiều này có dạng : \ ( i = I_ { 0 } cos ( \ omega t + \ varphi _ { i } ) \ )

Tần số góc của dòng điện này là : \ ( \ omega = 2 \ pi f = 2 \ pi. 50 = 100 \ pi ( rad / s ) \ )Tại thời gian t = 0,25. 10-2 s, dòng điện có cường độ tức thời i = I0 = 4 A, nên suy ra :\ ( I_ { 0 } cos ( 100 \ pi. 0 + \ varphi _ { i } ) = I_ { 0 } \ ) Hay \ ( cos ( \ frac { \ pi } { 4 } + \ varphi _ { i } ) = 1 \ )Suy ra : ( \ ( \ varphi _ { i } ) = – \ frac { \ pi } { 4 } rad \ ). Do đó biểu thức cường độ của dòng điện này là :\ ( i = I_ { 0 } cos ( 100 \ pi t – \ frac { \ pi } { 4 } ) ( A ) = 4 cos ( 100 \ pi t – \ frac { \ pi } { 4 } ) ( A ) \ )Tại thời gian t = 0 thì dòng điện có cường độ tức thời là :\ ( i = I_ { 0 } cos ( 100 \ pi. 0 – \ frac { \ pi } { 4 } ) ( A ) = \ frac { I_ { 0 } } { \ sqrt { 2 } } = \ frac { 4 } { \ sqrt { 2 } } = 2 \ sqrt { 2 } A \ ) \ ( \ approx 2,83 A \ ) .Vậy đồ thị cắt trục tung tại điểm có toạ độ ( 0 s, \ ( 2 \ sqrt { 2 } \ ) A ) .

Bài 3: Một khung dây có diện tích S = 60cm2   quay đều với vận tốc 20 vòng trong một giây. Khung đặt trong từ trường đều B = 2.10-2T.

Trục quay của khung vuông góc với những đường cảm ứng từ, lúc t = 0 pháp tuyến khung dây có hướng của .a. Viết biểu thức từ thông xuyên qua khung dây .b. Viết biểu thức suất điện động cảm ứng Open trong khung dây .

Hướng dẫn:

a. Chu kì : \ ( T = \ frac { 1 } { n_ { 0 } } = \ frac { 1 } { 20 } = 0,05 \ ) ( s ). Tần số góc : \ ( \ omega = 2 \ pi n_ { 0 } = 2 \ pi. 20 = 40 \ pi \ ) ( rad / s ) .\ ( \ Phi _ { 0 } = NBS = 1.2.10 ^ { – 2 }. 60.10 ^ { – 4 } = 12.10 ^ { – 5 } \ ) ( Wb ). Vậy \ ( \ Phi = 12.10 ^ { – 5 } cos40 \ pi t \ ) ( Wb )b. \ ( E_ { 0 } = \ omega \ Phi _ { 0 } = 40 \ pi. 12.10 ^ { – 5 } = 1,5. 10 ^ { – 2 } \ ) ( V )Vậy \ ( e = 1,5. 10 ^ { – 2 } sin40 \ pi t \ ) ( V ) Hay \ ( e = 1,5. 10 ^ { – 2 } cos ( 40 \ pi t – \ frac { \ pi } { 2 } ) \ ) ( V )

Bài 4: Một khung dây dẫn gồm N = 100 vòng quấn nối tiếp, diện tích mỗi vòng dây là  S = 60cm2. Khung dây quay đều với tần số 20 vòng/s, trong một từ trường đều có cảm ứng từ B = 2.10-2T. Trục quay của khung vuông góc với  .

a. Lập biểu thức của suất điện động cảm ứng tức thời .b. Vẽ đồ thị màn biểu diễn suất điện động cảm ứng tức thời theo thời hạn .

Hướng dẫn:

a. Chu kì : \ ( T = \ frac { 1 } { n_ { 0 } } = \ frac { 1 } { 20 } = 0,05 \ ) s. Tần số góc : \ ( \ omega = 2 \ pi n_ { 0 } = 2 \ pi. 20 = 40 \ pi \ ) ( rad / s )Biên độ của suất điện động : Eo = ωNBS = 40 π. 100.2.10 – 2.60.10 – 4 ≈ 1,5 VChọn gốc thời hạn lúc \ ( ( \ vec { B }, \ vec { n } ) = 0 \ Rightarrow \ varphi = 0 \ ) .

Suất điện động cảm ứng tức thời : \ ( e = E_ { 0 } sin \ omega t = 1,5 sin40 \ pi t \ ) ( V ) Hay \ ( e = 1,5 cos ( 40 \ pi t – \ frac { \ pi } { 2 } ) \ ) ( V ) .b. Đồ thị màn biểu diễn e theo t là đường hình sin :- Qua gốc tọa độ O .- Có chu kì T = 0,05 s- Biên độ Eo = 1,5 V .

Bài 5: Một khung dây dẫn có N = 100 vòng dây quấn nối tiếp, mỗi vòng có diện tích S = 50cm2. Khung dây được đặt trong từ trường đều B = 0,5T. Lúc t = 0, vectơ pháp tuyến của khung dây hợp với \(\overrightarrow{B}\) góc \(\varphi =\frac{\pi }{3}\). Cho khung dây quay đều với tần số 20 vòng/s quanh trục  (trục ∆ đi qua tâm và song song với một cạnh của khung) vuông góc với \(\overrightarrow{B}\) . Chứng tỏ rằng trong khung xuất hiện suất điện động cảm ứng e và tìm biểu thức của e theo t.

Hướng dẫn: Khung dây quay đều quanh trục ∆ vuông góc với cảm ứng từ \(\overrightarrow{B}\) thì góc hợp bởi vectơ pháp tuyến \(\vec{n}\) của khung dây  và \(\overrightarrow{B}\) thay đổi => từ thông qua khung dây biến thiên => Theo định luật cảm ứng điện từ, trong khung dây xuất hiện suất điện động cảm ứng.

Tần số góc : \ ( \ omega = 2 \ pi n_ { 0 } = 2 \ pi. 20 = 40 \ pi \ ) ( rad / s )Biên độ của suất điện động : \ ( E_ { 0 } = \ omega NBS = 40 \ pi. 100.0,5. 50.10 ^ { – 4 } \ approx 31,42 \ ) ( V )Chọn gốc thời hạn lúc : \ ( ( \ vec { n }, \ vec { B } ) = \ frac { \ pi } { 3 } \ )Biểu thức của suất điện động cảm ứng tức thời : \ ( e = 31,42 sin ( 40 \ pi t + \ frac { \ pi } { 3 } ) \ ) ( V )Hay \ ( e = 31,42 cos ( 40 \ pi t – \ frac { \ pi } { 6 } ) \ ) ( V )

Bài 6 (ĐH–2008: Một khung dây dẫn hình chữ nhật có 100 vòng, diện tích mỗi vòng 600 cm2, quay đều quanh trục đối xứng của khung với vận tốc góc 120 vòng/phút trong một từ trường đều có cảm ứng từ bằng 0,2T. Trục quay vuông góc với các đường cảm ứng từ. Chọn gốc thời gian lúc vectơ pháp tuyến của mặt phẳng khung dây ngược hướng với vectơ cảm ứng từ. Biểu thức suất điện động cảm ứng trong khung là

A. \ ( e = 48 \ pi sin ( 40 \ pi t – \ frac { \ pi } { 2 } ) ( V ) \ ) B. \ ( e = 4,8 \ pi sin ( 4 \ pi t + \ pi ) ( V ) \ )C. \ ( e = 48 \ pi sin ( 4 \ pi t + \ pi ) ( V ) \ ) D. \ ( e = 4,8 \ pi sin ( 40 \ pi t – \ frac { \ pi } { 2 } ) ( V ) \ )

HD: \(\Phi =BScos(\omega t+\pi )\Rightarrow e=-N.\Phi ‘=\)\(N\omega BS.sin(\omega t+\pi )=4,8sin(4\pi t+\pi )(V)\)

Bài 7:Một khung dây quay đều trong từ trường \(\overrightarrow{B}\) vuông góc với trục quay của khung với tốc độ n = 1800 vòng/ phút. Tại thời điểm t = 0, véctơ pháp tuyến \(\vec{n}\) của mặt phẳng khung dây hợp với \(\overrightarrow{B}\) một góc 300. Từ thông cực đại gởi qua khung dây là 0,01Wb. Biểu thức của suất điện động cảm ứng xuất hiện trong khung là :

  A. \(e=0,6\pi cos(30\pi t-\frac{\pi }{6})(Wb)\)                    B. \(e=0,6\pi cos(60\pi t-\frac{\pi }{3})(Wb)\)

  C.\(e=0,6\pi cos(60\pi t+\frac{\pi }{6})(Wb)\)                     D. \(e=60 cos(30 t+\frac{\pi }{3})(Wb)\)

 

Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:

Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay

Source: http://wp.ftn61.com
Category: Thủ Thuật