8+ công thức tổ hợp và bài tập có lời giải chi tiết

Ứng dụng nhiều trong trong thực tiễn nên tổ hợp được đưa vào toán 11 bậc trung học phổ thông. Thuộc chủ đề khó, dễ gây nhầm lẫn với hoán vị, chỉnh hợp nếu bắt đầu học hời hợt. Nếu bạn đang gặp thực trạng như vậy thì bài viết này là tài liệu hữu dụng giành cho bạn bởi những công thức tổ hợp và kim chỉ nan được mạng lưới hệ thống chuyên nghiệp, chi tiết cụ thể .

Để những em hiểu rõ hơn về tổ hợp tất cả chúng ta cùng tới phần triết lý cần nhớ của bài biết này nhé

1. Tổ hợp là gì?

Tổ hợp là cách chọn bất kì một nhóm a từ nhóm A. Như vậy a là con của A ( hay a ⊂ A)

Chú ý: Gọi n là số phần tử phân biệt của nhóm mẹ A thì n ≥ 1.

2. Công thức tổ hợp

Cách chọn bất kể nhóm con có k ( 1 ≤ k ≤ n ) thành phần từ nhóm mẹ A được gọi là một tổ hợp chập k của n thành phần .

• Kí hiệu: $C_n^k$
• Công thức:

Quy ước : USD C_n ^ 0 = 1 USD
Những đặc thù quan trọng :

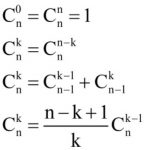
3. Bài tập tổ hợp có giải thuật cụ thể

Bài tập 1. (ĐỀ MINH HỌA LẦN 2-BDG 2019-2020) Có bao nhiêu cách chọn hai học sinh từ một nhóm có 10 học sinh

A. USD { 2 ^ { 10 } } USD
B. USD { 10 ^ 2 } USD
C. USD A_ { 10 } ^ 2 USD
D. USD C_ { 10 } ^ 2 USD
Hướng dẫn giải
Chọn 2 học viên bất kể trong số 10 học viên, số cách chọn bằng số tổ hợp chập 2 của 10 thành phần : USD C_ { 10 } ^ 2 USD
Chọn đáp án D .

Bài tập 2. Một đa giác lồi có n đỉnh ( với n > 3). Hỏi số Δ có 3 đỉnh là 3 đỉnh của đa giác lồi trên

A. n !
B. USD \ frac { { C_n ^ 3 } } { { 3 ! } } USD
C. USD C_n ^ 3 USD
D. USD A_n ^ 3 USD
Hướng dẫn giải
số Δ có 3 đỉnh là 3 đỉnh của đa giác lồi trên là số tổ hợp chập 3 của n thành phần. Khi đó số tam giác lập được sẽ là tổ hợp USD C_n ^ 3 USD
Chọn đáp án C .

Bài tập 3. Trên đường thẳng d$_1$ cho 5 điểm phân biệt, trên đường thẳng d$_2$ song song với đường thẳng d$_1$ cho n điểm phân biệt. Biết có tất cả 175 tam giác được tạo thành mà 3 đỉnh lấy từ (n + 5) điểm trên. Giá trị của n là

A. n = 8 .
B. n = 10 .
C. n = 9 .
D. n = 7 .
Hướng dẫn giải
Để tạo thành một tam giác cần 3 điểm phân biệt

Chọn đáp án D .

Bài tập 4. Trong hộp đựng bi có 4 viên màu xanh; 3 viên màu đỏ và 2 viên màu vàng. Chọn ngẫu nhiên 5 viên từ hộp đựng. Theo bạn có bao nhiêu cách chọn sao cho mỗi lần chọn đều có tối thiểu 1 viên xanh, 1 viên đỏ và 1 viên vàng.

A. 521 .
B. 16 .
C. 220 .
D. 98 .
Hướng dẫn giải
Số cách chọn ngẫu nhiên 5 viên bi : USD C_9 ^ 5 USD cách
Số cách chọn 5 viên bi chỉ có 2 màu : USD C_7 ^ 5 + C_6 ^ 5 + C_5 ^ 5 USD
Vậy số cách chọn 5 viên bi có cả 3 màu là USD C_9 ^ 5 – \ left ( { C_7 ^ 5 + C_6 ^ 5 + C_5 ^ 5 } \ right ) = 98 USD
Chọn đáp án D .

Bài tập 5. Trong một nhóm học sinh hỏi làm sao để chọn được 5 học sinh sao cho trong  5 học sinh đó sẽ có 1 tổ phó, 1 tổ trưởng và 3 học sinh có vai trò như nhau?

A. 45214 .
B. 954215 .
C. 310080 .
D. 15246 .
Hướng dẫn giải
Theo đề sẽ có 20 cách để chọn được ra 1 tổ trưởng từ 20 người trên .
Sau khi đã có được 1 tổ trưởng thì sẽ có 19 cách để chọn ra được 1 tổ phó từ 19 người còn lại
3 Thành viên còn lại sẽ có số cách là USD C_18 ^ 3 USD
Vậy hiệu quả cần tìm là USD 20.19. C_ { 18 } ^ 3 = 310080 USD
Chọn đáp án C .

Bài tập 6. Một mắc áo có 6 chiếc áo màu xanh, 5 chiếc áo màu đỏ và 4 chiếc áo màu vàng. Chọn ngẫu nhiên 5 chiếc áo sao cho có đủ cả ba màu. Số cách chọn là

A. 6254 .
B. 5427 .
C. 1452 .
D. 2170 .
Hướng dẫn giải
Số cách chọn 5 chiếc áo bất kỳ trong mắc là USD C_ { 15 } ^ 5 USD cách. Khi chọn bất kỳ thì gồm có những trường hợp sau

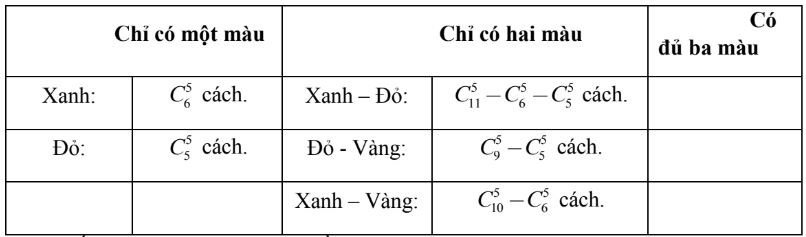
Suy ra số cách chọn thỏa mãn nhu cầu nhu yếu bài toán ( có đủ ba màu ) là

• $a = C_{15}^5 – C_6^5 + C_5^5$
• ${b = C_{11}^5 – C_6^5 – C_5^5}$
• ${c = C_9^5 – C_5^5}$
• ${d = C_{10}^5 – C_6^5}$

Khi đó: $a – \left[ {b + c + d} \right] = 2170$

Chọn đáp án D .
Nội dung về tổ hợp tạm dừng tại đây. Mọi góp ý hay để lại dưới phần phản hồi và đừng quên quay lại toanhoc.org để đón xem những chủ đề hay tiếp theo nhé .

Source: http://wp.ftn61.com
Category: Thủ Thuật