Công thức tính đường chéo hình bình hành chuẩn 100% [VD minh họa]

Bạn phân vân không biết công thức tính đường chéo hình bình hành như thế nào ? Tính chất đường chéo hình bình hành là gì ? Tất cả sẽ được chúng tôi giải đáp cụ thể trong bài viết dưới đây

Đường chéo hình bình hành là gì?

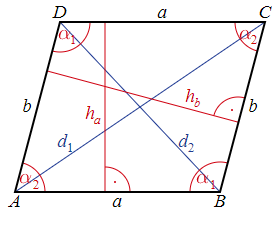
Đường chéo hình bình hành là đường nối những đỉnh đối lập của hình bình hành lại với nhau. Độ dài hai đường chéo của hình bình hành không bằng nhau và không vuông góc với nhau. Hai đường chéo cắt nhau tại trung điểm mỗi đường .

Công thức tính đường chéo hình bình hành

Đường chéo hình bình hành là căn bậc 2 của bình phương độ dài những cạnh trừ 2 lần độ dài những cạnh nhân cos những góc được tạo bởi hai cạnh kề nhau của hình bình hành .

d1,2 = √a2 + b2 – 2abcosα1,2

Trong đó :

• d1,2 là đường chéo hình bình hành
• a, b là độ dài các cạnh của hình bình hành
• α1, α2 là các góc được tạo bởi 2 cạnh kề nhau của hình bình hành
• α1 + α2 = 180ο

Tham khảo thêm :

Bài tập tính đường chéo hình bình hành

Ví dụ 1 : Hình bình hành ABCD có AB = 6 cm, BC = 7 cm, BD = 8 cm. Tính AC .
Lời giải
Gọi I là giao điểm của hai đường chéo AC và BD => AI là đường trung tuyến của tam giác ABD
Tính độ dài AI : Áp dụng công thức tính đường trung tuyến
=> AI2 = ( AB2 + AD2 ) : 2 – ( BD2 : 4 )
Tính độ dài AC : Vì I là trung điểm của AC nên AC = 2. AI
Ví dụ 2 : Cho hình bình hành ABCD, Gọi J, K theo thứ tự là trung điểm của cạnh CD và AB. Biết đường chéo BD cắt AJ, UK theo thứ tự là MN. Chứng minh rằng DM = MN = NB

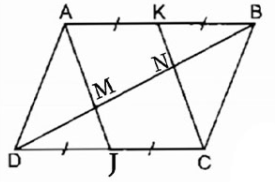
Ta có : AB = CD ( Theo đặc thù hình bình hành )
AK = ½ AB
CJ = ½ CD
AK = CJ ( 1 )
Mặt khác : AB / / CD
AK / / CJ ( 2 )
Từ ( 1 ) Và ( 2 ) ta được tứ giác AKCJ là hình bình hành bởi có 1 cặp cạnh đối song song và bằng nhau .
AJ / / CK
Trong ∆ ABM ta có :
K là trung điểm của cạnh AB
AJ / / CK hay KN / / AM nên ta được BN = MN ( theo đặc thù đường trung bình của hình tam giác )
Trong đó ∆ DCN ta có :
J là trung điểm của cạnh DC
AJ / / CK hay JM / / CN nên DM = MN ( Theo đặc thù đường trung bình của hình tam giác
DM = MN = NB
Ví dụ 3 : Cho hình bình hành MNPQ biết MN = 12 cm, NP = 14 cm, PQ = 16 cm. Hỏi MP .

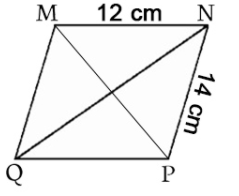
Lời giải :
Gọi K là giao điểm của đường chéo MP và NP
MK là đường trung tuyến của tam giác MNQ
Áp dụng theo công thức tính đường trung tuyến ta được

MK2 = (MN2 + MQ2) : 2 – (NQ2 : 4) = (142 + 122) : 2 – (162 :4) = 106 => MK = √106

Vì K là trung điểm của cạnh MP nên MP = 2MK = 2 √ 106
Ví dụ 4 : Cho hình bình hành MNPQ biết chu vi hình bình hành bằng 20 dm, chu vi tam giác MNQ bằng 18 dm. Tính độ dài cạnh NQ .

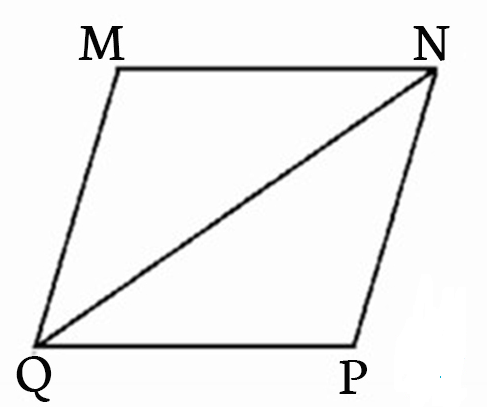
Lời giải :
Chu vi hình bình hành bằng MNPQ = 10 dm => ( MN + PQ ) x 2 = 20 dm
MN + MQ = 20 : 2 = 10 dm
Chu vi của ∆ MNQ = MN + MQ + NQ = 18 dm
NQ = 18 – ( MN + MQ )
= 18 – 10
= 8 dm

Ví dụ 5: Cho hình bình hành ABCD biết độ dài cạnh AD = 8cm, cạnh AC = 9.5cm, góc 𝛼= 60°. Hỏi độ dài cạnh DC.
Lời giải tham khảo:

Gọi độ dài cạnh DC cần tìm là a ( a > 0, cm )
Áp dụng công thức ta có :
AC² = AD² + CD² – 2. AD.CD.cos 𝛼
⇔ 9.5 ² = 8 ² + a² – 2.8. CD.cos 60 °
⇔ a² – 8 a – 26.25 = 0
⇔ a = 10.5 ( tmdk ) hoặc a = – 2.5 ( Loại )
Vậy độ dài cạnh CD cần tìm là 10.5 cm
Sau khi đọc xong bài viết của chúng tôi những bạn hoàn toàn có thể biết công thức tính đường chéo hình bình hành để vận dụng vào làm những bài tập đơn thuần và đúng chuẩn nhé

5
/
5
(
1

bình chọn

)

Source: http://wp.ftn61.com
Category: Thủ Thuật