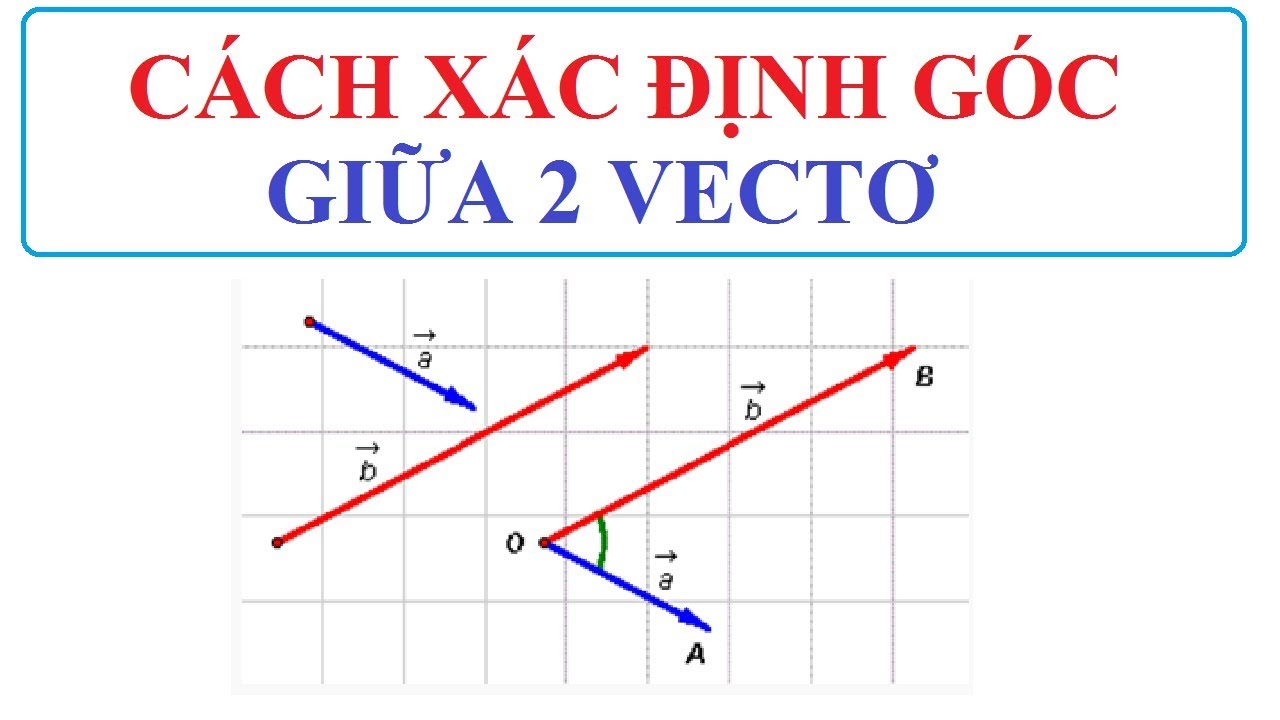
Vectơ, cụ thể là hướng của vectơ và góc mà chúng được định hướng, có tầm quan trọng đáng kể trong hình học vectơ và vật lý. Nếu có hai vectơ, giả sử a và b trong một mặt phẳng sao cho các đầu của cả hai vectơ nối với nhau, thì tồn tại một góc nào đó giữa chúng và góc giữa hai vectơ đó được xác định là:
“ Góc giữa hai vectơ là góc ngắn nhất mà tại đó quay bất kỳ của hai vectơ nào về vectơ kia sao cho cả hai vectơ có cùng phương.”
Hơn nữa, cuộc thảo luận này tập trung vào việc tìm góc giữa hai vectơ chuẩn, có nghĩa là gốc của chúng ở (0, 0) trong mặt phẳng xy.
Bạn đang đọc: Giải thích và Ví dụ
Trong chủ đề này, tất cả chúng ta sẽ bàn luận ngắn gọn về những điểm sau :
- Góc giữa hai vectơ là gì?
- Làm thế nào để tìm ra góc giữa hai vectơ?
- Góc giữa hai vectơ 2-D.
- Góc giữa hai vectơ 3-D.
- Các ví dụ.
- Các vấn đề.
Tóm tắt nội dung bài viết
Góc giữa hai vectơ
Các vectơ được định hướng theo các hướng khác nhau trong khi tạo thành các góc khác nhau. Góc này tồn tại giữa hai vectơ và chịu trách nhiệm xác định vị trí của các vectơ.
Góc giữa hai vectơ có thể được tìm thấy bằng cách sử dụng phép nhân vectơ. Có hai kiểu nhân vectơ, tức là tích vô hướng và tích chéo .
Tích vô hướng là tích hoặc phép nhân của hai vectơ sao cho chúng tạo ra một đại lượng vô hướng. Như tên cho thấy, tích vectơ hoặc tích chéo tạo ra một đại lượng vectơ do tích hoặc phép nhân của hai vectơ .
Ví dụ, nếu tất cả chúng ta nói về hoạt động của quả bóng đánh tennis, vị trí của nó được miêu tả bởi một vectơ vị trí và hoạt động bởi một vectơ tốc độ có độ dài biểu lộ vận tốc của quả bóng. Hướng của vectơ lý giải hướng hoạt động. Tương tự, động lượng của quả bóng cũng là một ví dụ về đại lượng vectơ có khối lượng nhân với tốc độ .
Đôi khi tất cả chúng ta phải giải quyết và xử lý hai vectơ công dụng lên một đối tượng người dùng nào đó, do đó góc của vectơ là rất quan trọng. Trong quốc tế thực, bất kể mạng lưới hệ thống thao tác nào cũng tích hợp 1 số ít vectơ được link với nhau và tạo 1 số ít góc với nhau trong mặt phẳng nhất định. Vectơ hoàn toàn có thể là hai chiều hoặc 3 chiều. Do đó, cần phải đo lường và thống kê góc giữa những vectơ .
Đầu tiên tất cả chúng ta hãy bàn luận về những loại sản phẩm vô hướng .

Góc giữa hai vectơ sử dụng sản phẩm chấm
Xét hai vectơ a , b cách nhau một góc θ. Khi đó theo công thức của sản phẩm chấm là:
ab = | a | | b | .cosθ
trong đó ab là tích chấm của hai vectơ. | a | và | b | là độ lớn của vectơ a và b, và θ là góc giữa chúng.
Để tìm góc giữa 2 vectơ, tất cả chúng ta sẽ mở màn với công thức của tích số chấm cho cosin của góc θ .
Theo công thức của tích vô hướng ,
ab = | a | | b | .cosθ
Điều này nói lên rằng tích số chấm của hai vectơ a và b bằng độ lớn của hai vectơ a và b nhân với cosin của góc. Để tìm góc giữa hai vectơ, a và b, tất cả chúng ta sẽ giải ra góc θ ,
cosθ = ab / | a |. | b |
θ = arccos ( ab / | a |. | b |)
Vì vậy, θ là góc giữa hai vectơ .
Nếu vectơ a =
Khi đó tích chấm giữa hai vectơ a và b được cho là,
ab =
ab = a x .b x + a y .b y
Ở đây, chúng ta có thể có một ví dụ về công việc được thực hiện vì công việc được thực hiện được định nghĩa là lực tác dụng để di chuyển một vật thể ở một khoảng cách nào đó. Cả hai lực lượng và dịch chuyển là vectơ, và chấm sản phẩm của họ mang lại một số lượng vô hướng, tức là ., Làm việc. Công việc được thực hiện là tích số chấm của lực và độ dịch chuyển, có thể được định nghĩa là,
- d = | F | | d | cos (θ)
Trong đó θ là góc giữa lực và độ dời. Ví dụ, nếu chúng ta coi một chiếc ô tô đang chuyển động trên đường, bao phủ một khoảng cách nào đó theo một hướng nhất định, thì một lực tác dụng lên ô tô, trong khi lực tạo nên một góc θ với độ dời.
Sau đây là một số ít thuộc tính của mẫu sản phẩm chấm :
- Tích có tính chất giao hoán.
- Nó có bản chất phân phối so với phép cộng vectơ:
- (b + c) = (a. b) + (a. c)
- Nó không có tính chất liên kết.
- Một đại lượng vô hướng có thể được nhân với tích số chấm của hai vectơ.
- (a. b) = (ca). b = a. (cb)
- Tích số chấm là cực đại khi hai vectơ khác không song song với nhau.
- Hai vectơ vuông góc với nhau nếu và chỉ khi a. b = 0 là tích chấm là cosin của góc giữa hai vectơ a và b và cos (90) = 0.
- Đối với vectơ đơn vị
Tôi. i = 1
- j = 1
- k = 1
- Phép nhân điểm không tuân theo luật hủy
- b = a. c
- (b – c) = 0
Tương tự, tất cả chúng ta cũng hoàn toàn có thể sử dụng những mẫu sản phẩm chéo cho mục tiêu này .
Công thức của tích chéo như sau :
axb = | a |. | b | .sinθ. n
Đầu tiên tất cả chúng ta hãy nhìn nhận góc giữa hai vectơ bằng cách sử dụng tích số chấm .
ví dụ 1
Tìm góc giữa hai vectơ có độ lớn bằng nhau và độ lớn của vectơ tác dụng của chúng tương tự với độ lớn của một vectơ bất kể trong số những vectơ đã cho .
Giải pháp
Chúng ta hãy xem xét hai vectơ, Một và B, và các kết quả của hai vectơ là R .
Do đó, theo điều kiện kèm theo được đưa ra trong câu hỏi :
| A | = | B | = | R |
Bây giờ, theo định luật cosin ,
| R | ^ 2 = | A | ^ 2 + | B | ^ 2 + 2 | A | | B |. cos ( θ )
Kể từ, | A | = | B | = | R |
| A | ^ 2 = | A | ^ 2 + | A | ^ 2 + 2 | A | | A |. cos ( θ )
| A | ^ 2 = | A | ^ 2 + | A | ^ 2 + | A | ^ 2. cos ( θ )
| A | ^ 2 = 2 | A | ^ 2 + | A | ^ 2. cos ( θ )
| A | ^ 2 = 2 | A | ^ 2 ( 1 + cos ( θ ) )
| A | ^ 2/2 | A | ^ 2 = ( 1 + cos ( θ ) )
50% = 1 + cos ( θ )
50% – 1 = cos ( θ )
– 1 / 2 = cos ( θ )
θ = cos – 1 ( – 1 / 2 )
θ = 120 º
Vậy góc giữa hai vectơ có hoành độ bằng nhau thì bằng 120 º .
Ví dụ 2
Tìm góc giữa hai vectơ có độ lớn bằng nhau. Ngoài ra, hãy giám sát độ lớn của vectơ tác dụng .
Giải pháp
Nó được cho rằng ,
| A | = | B |
Sử dụng pháp luật của cosin để tính toán độ lớn của vector kết quả R .
| R | ^ 2 = | A | ^ 2 + | B | ^ 2 + 2 | A | | B |. cos ( θ )
| R | = √ ( | A | ^ 2 + | B | ^ 2 + 2 | A | | B |. Cos ( θ ) )
| R | = √ | A | ^ 2 + | A | ^ 2 + 2 | A | | A |. cos ( θ )
| R | = √ ( 2 | A | ^ 2 + 2 | A | ^ 2. Cos ( θ ) )
| R | = √ ( 2 | A | ^ 2 ( 1 + cos ( θ ) ) )
Áp dụng nhận dạng nửa góc ,
| R | = √ ( 4A ^ 2 cos ^ 2 ( θ / 2 ) )
| R | = 2 A cos ( θ / 2 )
Bây giờ, để đo lường và thống kê góc tác dụng α mà nó sẽ tạo ra với vectơ tiên phong ,
tan α = ( A sin θ ) / ( A + A cos θ )
tan α = ( 2 A cos ( θ / 2 ). sin ( θ / 2 ) / ( 2 A cos 2 ( θ / 2 ) )
tan α = tan ( θ / 2 )
α = θ / 2
Do đó, điều này cho thấy rằng hiệu quả sẽ chia góc giữa hai vectơ có độ lớn bằng nhau .
Ví dụ 3
Tìm góc giữa hai vectơ đã cho .
A = 6 i + 5 j + 7 k
B = 3 i + 8 j + 2 k
Giải pháp
Sử dụng công thức của loại sản phẩm chấm ,
- B = | A | | B | . cos (θ)
Tìm hoành độ của A và B.
Vì vậy, độ lớn của A được cho là,
| A | = √ ( ( 6 ) ^ 2 + ( 5 ) ^ 2 + ( 7 ) ^ 2 )
| A | = √ ( 36 + 25 + 49 )
| A | = √ ( 110 )
Độ lớn của B được cho là,
| B | = √ ( ( 3 ) ^ 2 + ( 8 ) ^ 2 + ( 2 ) ^ 2 )
| B | = √ ( 9 + 64 + 4 )
| B | = √ ( 77 )
Bây giờ, việc tìm kiếm mẫu sản phẩm chấm ,
AB = (6 i + 5 j +7 k ). (3 i + 8 j + 2 k )
AB = 18 + 40 + 14
AB = 72
Xem thêm: Làm Thế Nào Để Học Giỏi Hóa 9?
Đưa vào công thức của loại sản phẩm chấm ,
72 = ( √ ( 110 ) ). ( √ ( 77 ) ). cos ( θ )
72 / ( √ ( 110 x 77 ) ) = cos ( θ )
cos ( θ ) = 0,78
θ = cos – 1 ( 0,78 )
θ = 51,26 º
Ví dụ 4
Tìm góc giữa hai vectơ đã cho
A = <4, 3, 2>
B = <1, 2, 5>
Giải pháp
Sử dụng công thức của loại sản phẩm chấm ,
- B = | A | | B | . cos (θ)
Tìm hoành độ của A và B.
Vì vậy, độ lớn của A được cho là,
| A | = √ ( ( 4 ) ^ 2 + ( 3 ) ^ 2 + ( 2 ) ^ 2 )
| A | = √ ( 16 + 9 + 4 )
| A | = √ ( 29 )
Độ lớn của B được cho là,
| B | = √ ( ( 1 ) ^ 2 + ( 2 ) ^ 2 + ( 5 ) ^ 2 )
| B | = √ ( 1 + 4 + 25 )
| B | = √ ( 30 )
Bây giờ, việc tìm kiếm mẫu sản phẩm chấm ,
AB = <4, 3, 2>. <1, 2, 5>
AB = 4 + 6 + 10
AB = 20
Đưa vào công thức của loại sản phẩm chấm ,
20 = ( √ ( 29 ) ). ( √ ( 30 ) ). cos ( θ )
20 / ( √ ( 29 x 30 ) ) = cos ( θ )
cos ( θ ) = 0,677
θ = cos – 1 ( 0,677 )
θ = 42,60 º
Góc giữa hai vectơ sử dụng sản phẩm chéo
Một phương pháp khác để tìm góc giữa hai vectơ là tích chéo. Sản phẩm chéo được định nghĩa là:
“Vectơ vuông góc với cả vectơ và hướng được cho bởi quy tắc bàn tay phải.
Vì vậy, loại sản phẩm chéo được màn biểu diễn bằng toán học là ,
axb = | a | | b | . sin (θ) n
Trong đó θ là góc giữa hai vectơ, | a | và | b | là độ lớn của hai vectơ a và b, và n là vectơ đơn vị vuông góc với mặt phẳng chứa hai vectơ a và b theo phương được cho bởi quy tắc bàn tay phải.
Xét hai vectơ a và b có đuôi nối với nhau và do đó tạo thành một góc θ nào đó. Để tìm góc giữa hai vectơ, chúng ta sẽ vận dụng công thức tích chéo ở trên.
( axb ) / (| a |. | b |) = sin (θ)
Nếu các vectơ a và b đã cho song song với nhau thì theo công thức nêu trên, tích chéo sẽ bằng 0 vì sin (0) = 0. Trong khi xử lý tích chéo, chúng ta phải cẩn thận với các hướng.

Sau đây là một số ít đặc tính của loại sản phẩm chéo :
- Sản phẩm chéo có bản chất chống ung thư.
- Tích chéo tự của các vectơ bằng không.
A x A = 0
- Sản phẩm chéo được phân phối hơn là bổ sung vectơ
a x ( b + c) = ( a x b ) + ( a x c )
- Nó không có tính chất liên kết.
- Một đại lượng vô hướng có thể được nhân với tích số chấm của hai vectơ.
- ( a x b ) = (c a ) x b = a x (c b )
- Tích của dấu chấm là cực đại khi hai vectơ khác không vuông góc với nhau.
- Hai vectơ song song (tức là nếu góc giữa hai vectơ bằng 0 hoặc 180) với nhau nếu và chỉ khi axb = 1 là tích chéo là sin của góc giữa hai vectơ a và b và sin (0) = 0 hoặc sin ( 180) = 0.
- Đối với vectơ đơn vị
ixi = 0
jxj = 0
kxk = 0
ixj = k
jxk = tôi
kxi = j
- Phép nhân chéo không tuân theo luật hủy bỏ
axb = axc
ax ( b – c ) = 0
Đây là một số ít thuộc tính của loại sản phẩm chéo .
Hãy giải 1 số ít ví dụ để hiểu khái niệm này .
Ví dụ 5
Tính góc giữa hai vectơ sao cho chúng là vectơ đơn vị a và b trong đó a x b = 1/3 i + 1/4 j .
Giải pháp
Kể từ, nó đã cho ,
| a | = | b | = 1
Trong khi ,
| axb | = √ ( ( 1/3 ) ^ 2 + ( 1/4 ) ^ 2 ) = 1/5
Bây giờ, đưa vào công thức ,
| axb | = | a | | b | tội lỗi θ
1/5 = ( 1 ) ( 1 ) sin θ
θ = sin – 1 ( 1/5 )
θ = 30 º
Ví dụ 6
Tính góc giữa hai vectơ sao cho a = 3 i – 2 j – 5 k và b = i + 4 j – 4 k trong đó a x b = 28 i + 7 j + 14 k .
Giải pháp
Vì vậy, độ lớn của vectơ a được cho là,
| a | = √ ( ( 3 ) ^ 2 + ( – 2 ) ^ 2 + ( – 5 ) ^ 2 )
| a | = √ ( 9 + 4 + 25 )
| a | = √ ( 38 )
Độ lớn của vectơ b được cho là,
| b | = √ ( ( 1 ) ^ 2 + ( 4 ) ^ 2 + ( – 4 ) ^ 2 )
| b | = √ ( 1 + 16 + 16 )
| b | = √ ( 33 )
Trong khi, độ lớn của axb được cho là,
| axb | = √ ( ( 28 ) 2 + ( 7 ) 2 + ( 14 ) )
| axb | = √ ( 1029 )
| axb | = 32,08
Bây giờ, đưa vào công thức ,
| axb | = | a | | b | tội lỗi θ
32,08 = ( √ ( 38 ) ) ( √ ( 33 ) ) sin θ
sin θ = 32,08 / ( √ ( 38 ) ) ( √ ( 33 ) )
θ = 64,94 º
Vậy góc giữa hai vectơ a và b là θ = 64,94º .
Vectơ hoàn toàn có thể là cả hai chiều cũng như ba chiều. Phương pháp tìm góc giống nhau trong cả hai trường hợp. Sự độc lạ duy nhất là vectơ 2 – D có hai tọa độ x và y trong khi vectơ 3 – D có ba tọa độ x, y và z. Các ví dụ được xử lý ở trên sử dụng cả vectơ 2 – D và 3 – D .
Vấn đề thực hành
- Cho rằng | A | = 3 và | B | = 5 trong đó a. b = 7,5, tìm góc giữa hai vectơ.
- Tính góc giữa hai vectơ 3i + 4j – k và 2i – j + k.
- Tính góc giữa hai vectơ sao cho a = 2 i – 3 j + 1 k và b = -1 i + 0 j + 5 k trong đó a x b = -15 i – 11 j – 3 k .
- Tính góc giữa hai vectơ sao cho a = 2 i + 3 j + 5 k và b = i + 6 j – 4 k trong đó a . b = 0.
- Tìm góc giữa các vectơ đã cho t = (3, 4) và r = (−1, 6).
- Vectơ R của hai vectơ A và B có cùng độ lớn sẽ là bao nhiêu nếu góc giữa chúng bằng 90 o .
Câu trả lời
- 60 °
- 85,40 °
- 81,36 °
- 90 °
- 36,30 °
- 90 °
Xem thêm:
Xem thêm: Làm Thế Nào Để Active Windows 7
Cách tìm độ lớn vectơ đơn giản nhất cho bạn
Chi tiết cách tìm một đơn vị Vector chỉ trong giây lát
Source: http://wp.ftn61.com
Category: Thủ Thuật


Để lại một bình luận