Hệ thức lượng trong tam giác vuông, thường chi tiết, đầy đủ, ví dụ áp dụng

Các bài toán về hệ thức lượng trong tam giác vuông thường Open ở rất nhiều những kỳ thi lớp 10 trung học phổ thông chính vì thế những bạn cần phải lắm rõ để hoàn toàn có thể làm bài thật tốt. Ở bài viết này chúng tôi xin gửi đến những bạn triết lý về hệ thức lượng trong tam giác vuông mong sẽ giúp những em mạng lưới hệ thống lại kỹ năng và kiến thức cũng như biết cách xử lí những bài toán trong dạng toán này .

Nhắc lại những hệ thức lượng trong tam giác vuông, thường

1. CÁC HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG

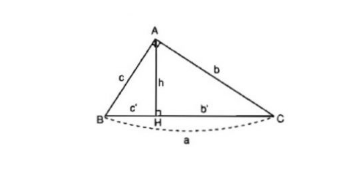
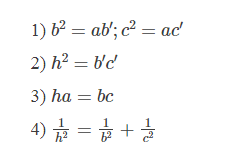
2. TÍ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN TRONG TAM GIÁC VUÔNG

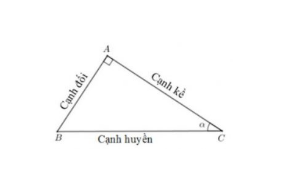
Cách ghi nhớ:

Để ý những vần âm đầu : Sin = Đối / Huyền, Cos = Kề / Huyền, Tan = Đối / Kề, Cot = Kề / Đối nên cách ghi nhớ là : “ Sao Đi Học, Cứ Khóc Hoài, Thôi Đừng Khóc, Có Kẹo Đây. ”

3. Định lý Cosin

Trong một tam giác bất kỳ, bình phương một cạnh bằng tổng những bình phương của hai cạnh còn lại trừ đi hai lần tích của hai cạnh đó nhân với Cosin của góc xen giữa chúng .

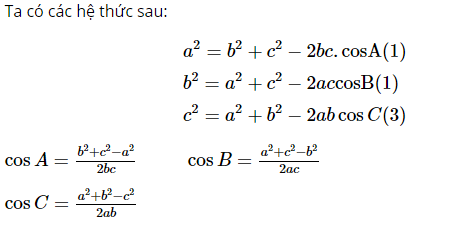
Ví dụ áp dụng thực tế : Tính độ dài đường trung tuyến của tam giác:

4. Định lý Sin

Trong tam giác ABCABC bất kể, tỉ số giữa một cạnh và sin của góc đối lập với cạnh đó bằng đường kính của đường tròn ngoại tiếp tam giác, nghĩa là :

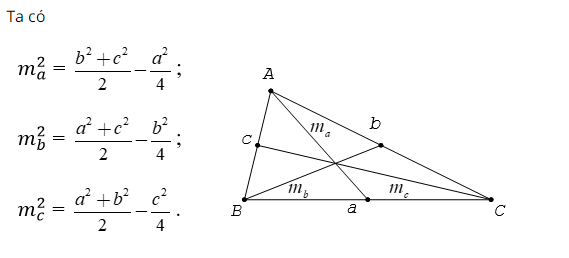
5. Độ dài đường trung tuyến

Cho tam giác ABC có ma, mb, mc lần lượt là những trung tuyến kẻ từ A, B, C .

6. Công thức tính diện tích quy hoạnh tam giác

Cho tam giác ABC có
+ ) ha, hb, hc là độ dài đường cao lần lượt tương ứng với những cạnh BC, CA, AB ;
+ ) R là nửa đường kính đường tròn ngoại tiếp tam giác ;
+ ) r là nửa đường kính đường tròn nội tiếp tam giác ;

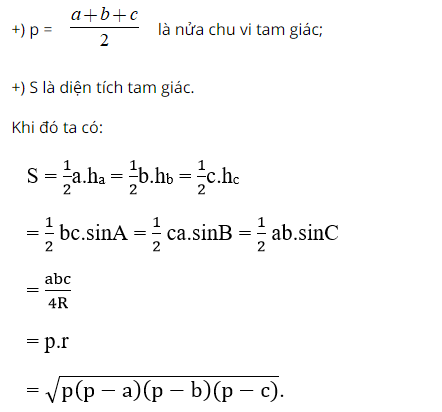
7. Ví dụ trong thực tiễn tính theo hệ thức lượng trong tam giác vuông

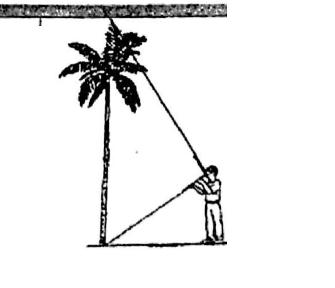
Ví dụ 1 : Một người thợ sử dụng thước ngắm có góc vuông đề đo chiều cao của một cây dừa, với các kích thước đo được như hình bên. Khoảng cách từ vị trí gốc cây đến vị trí chân của người thợ là 4,8m và từ vị trí chân đứng thẳng trên mặt đất đến mắt của người ngắm là l,6m. Hỏi với các kích thước trên thì người thợ đo được chiều cao của cây đó là bao nhiêu? (làm tròn đến mét).

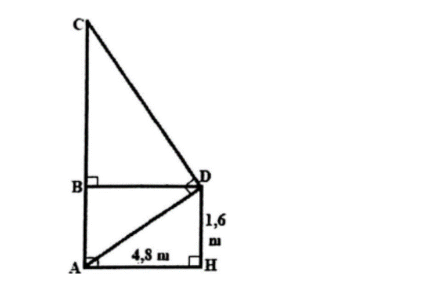
Bài giải:

Hình vẽ minh họa bài toán :

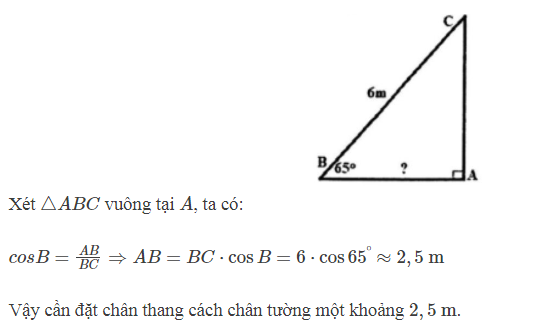
Ví dụ 2 : Trường bạn An có một chiếc thang dài 6 mét. Cần đặt chân thang cách chân tường một khoảng cách bằng bao nhiêu để nó tạo được với mặt đất một góc “an toàn” là 65∘ (tức là đảm bảo thang không bị đổ khi sử dụng).

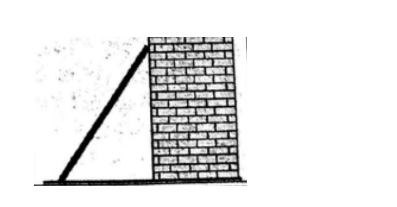
Bài giải:

Hình vẽ minh họa bài toán :

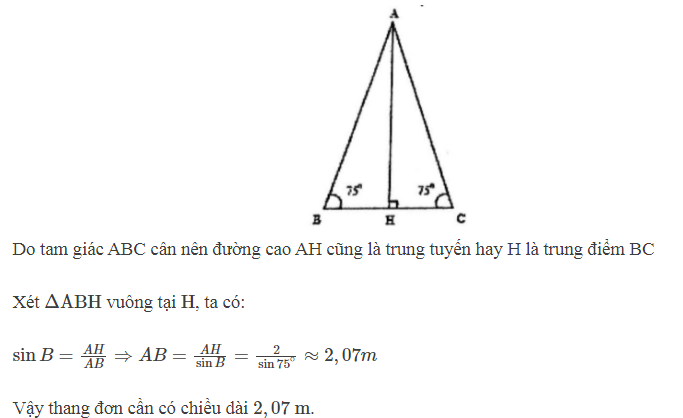
Ví dụ 3 : Thang xếp chữ A gồm 2 thang đơn tựa vào nhau. Để an toàn, mỗi thang đon tạo với mặt đất một góc khoảng 750. Nếu muốn tạo một thang xếp chữ A cao 2 m tính từ mặt đất thì mỗi thang đơn phải dài bao nhiêu ?

BÀI GIẢI:

Hình vẽ minh họa bài toán :

Sau khi đọc xong bài viết của chúng tôi bạn hoàn toàn có thể mạng lưới hệ thống lại kỹ năng và kiến thức về hệ thức lượng trong tam giác. Ngoài ra, những bạn hoàn toàn có thể tìm hiểu thêm tính cạnh huyền trong tam giác vuông tại : https://samsungcontest.com.vn/cong-thuc-tinh-canh-huyen-trong-tam-giac-vuong/

5/5 – ( 1 bầu chọn )

Source: http://wp.ftn61.com
Category: Thủ Thuật