Lý thuyết Toán 11 Bài 3: Một số phương trình lượng giác thường gặp
Bài giảng Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (T1)
Bài giảng Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (T2)
A. Lý thuyết
I. Phương trình bậc nhất đối với một hàm số lượng giác
1. Định nghĩa.
Phương trình bậc nhất đối với một hàm số lượng giác là phương trình có dạng:
at + b = 0 ( 1 )
Trong đó ; a, b là những hằng số ( a ≠ 0 ) và t là một trong những hàm số lượng giác .
– Ví dụ 1.
a ) – 3 sinx + 8 = 0 là phương trình bậc nhất so với sinx .
b ) 6 cotx + 10 = 0 là phương trình bậc nhất so với cotx .
2. Cách giải
Chuyển vế rồi chia hai vế của phương trình ( 1 ) cho a, ta đưa phương trình ( 1 ) về phương trình lượng giác cơ bản .
– Ví dụ 2. Giải các phương trình sau:
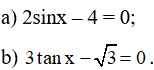
Lời giải:
a ) Từ 2 sinx – 4 = 0, chuyển vế ta có : 2 sinx = 4 ( 2 )
Chia 2 vế của phương trình ( 2 ) cho 2, ta được : sinx = 2 .
Vì 2 > 1 nên phương trình đã cho vô nghiệm .
b ) Từ 3 tanx − 3 = 0, chuyển vế ta có : 3 tanx = 3 ( 3 )
Chia cả 2 vế của phương trình ( 3 ) cho ta được : tanx = 33 .
⇔ tanx = tan π6 ⇔ x = π6 + kπ ; k ∈ ℤ
3. Phương trình đưa về phương trình bậc nhất đối với một hàm số lượng giác.
– Phương pháp:
Sử dụng những công thức biến hóa lượng giác đã được học để đưa về phương trình bậc nhất so với hàm số lượng giác hoặc đưa về phương trình tích để giải phương trình .
– Ví dụ 3. Giải các phương trình:
a ) sin2x – cosx = 0 ;
b ) – 4 sinx. cosx. cos2x = 1 .
Lời giải:
a ) Ta có : sin2x – cosx = 0
2 sinx. cosx – cosx = 0
cosx. ( 2 sinx – 1 ) = 0
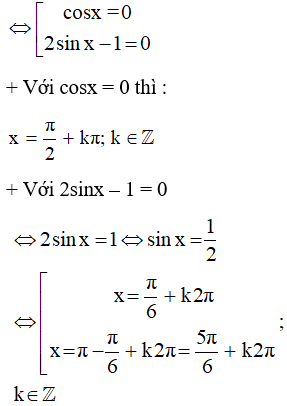
Vậy phương trình đã cho có những nghiệm là : x = π2 + kπ ; x = π6 + k2π và x = 5 π6 + k2π ; k ∈ ℤ .

II. Phương trình bậc hai đối với một hàm số lượng giác
1. Định nghĩa.
Phương trình bậc hai so với một hàm số lượng giác là phương trình có dạng :
at2 + bt + c = 0
Trong đó a ; b ; c là những hằng số ( a ≠ 0 ) và t là một trong những hàm số lượng giác .
– Ví dụ 4.
a ) 3 cos2x – 5 cosx + 2 = 0 là phương trình bậc hai so với cosx .
b ) – 10 tan2x + 10 tanx = 0 là phương trình bậc hai so với tanx .
2. Cách giải.
Đặt biểu thức lượng giác làm ẩn phụ và đặt điều kiện kèm theo cho ẩn phụ ( nếu có ) rồi giải phương trình theo ẩn phụ này .
Cuối cùng ta đưa về việc giải những phương trình lượng giác cơ bản .
– Ví dụ 5. Giải phương trình: 2cos2x – 4 cosx = 0.
Lời giải:
Đặt t = cosx với điều kiện kèm theo : – 1 ≤ t ≤ 1 .
Ta được phương trình bậc hai ẩn t là : 2 t2 – 4 t = 0 ⇔ t = 0 t = 2
Trong hai nghiệm này chỉ có nghiệm t = 0 thỏa mãn nhu cầu .
Với t = 0 thì cos x = 0
⇔ x = π2 + kπ ; k ∈ ℤ
Vậy phương trình đã cho có nghiệm là x = π2 + kπ ; k ∈ ℤ .
3. Phương trình đưa về dạng phương trình bậc hai đối với một hàm số lượng giác.
– Phương pháp:
Sử dụng những công thức lượng giác đã học để đổi khác đưa về dạng phương trình bậc hai so với một hàm số lượng giác .
– Ví dụ 6. Giải phương trình 3sin2x – 6cosx – 3 = 0.
Lời giải:
Vì sin2x = 1 – cos2x nên phương trình đã cho tương tự :
3 ( 1 – cos2x ) – 6 cosx – 3 = 0
– 3 cos2 x – 6 cosx = 0 ( * )
Đăt t = cosx với điều kiện kèm theo : – 1 ≤ t ≤ 1, phương trình ( * ) trở thành :
– 3 t2 – 6 t = 0 ⇔ t = 0 t = − 2 .
Trong hai nghiệm này, chỉ có nghiệm t = 0 thỏa mãn nhu cầu .
Với t = 0 thì ; cosx = 0 v ⇔ x = π2 + kπ ; k ∈ ℤ .
Vậy phương trình đã cho có nghiệm là x = π2 + kπ ; k ∈ ℤ .
– Ví dụ 7. Giải phương trình: sin2x – 3sinx. cosx + 2cos2x = 0 (1).
Lời giải:
+ Nếu cosx = 0 thì sin2x = 1 nên phương trình ( 1 ) có :
VT ( 1 ) = 1 và VP ( 1 ) = 0
Suy ra, cos x = 0 không thỏa mãn nhu cầu phương trình ( 1 ). Vậy cosx ≠ 0 .
+ Vì cosx ≠ 0 nên chia hai vế của phương trình ( 1 ) cho cos2 x, ta được :
tan2x – 3 tanx + 2 = 0 ( 2 )
Đặt t = tanx, phương trình ( 2 ) trở thành : t2 – 3 t + 2 = 0
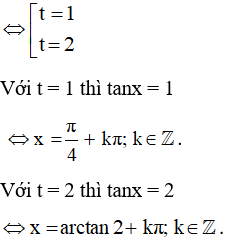
Vậy phương trình đã cho có những nghiệm là
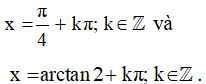
III. Phương trình bậc nhất đối với sinx và cosx.
1. Công thức biến đổi biểu thức a.sinx + b.cosx
Ta có công thức đổi khác sau :
asinx + b.cosx = a 2 + b2. sin ( x + α ) 1
Trong đó ;
cosα = aa2 + b2 ; sin α = ba2 + b2
2. Phương trình dạng: asinx + b.cosx = c.
Xét phương trình : asinx + bcosx = c ( 2 )
Với a ; b ; c ; a, b không đồng thời bằng 0 .
– Nếu a = 0 ; b ≠ 0 hoặc a ≠ 0 ; b = 0 phương trình ( 2 ) hoàn toàn có thể đưa ngay về phương trình lượng giác cơ bản .
– Nếu a ≠ 0 ; b ≠ 0, ta vận dụng công thức ( 1 ) .
Ví dụ 8. Giải phương trình: 3sinx− cosx = 2.
Lời giải:
Theo công thức ( 1 ) ta có :
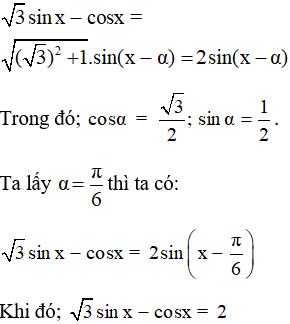
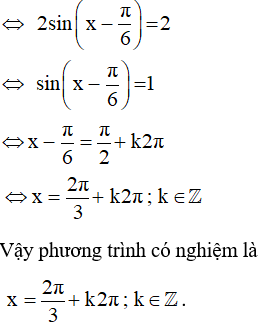
B. Bài tập tự luyện
Bài 1. Giải các phương trình sau:
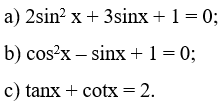
Lời giải:

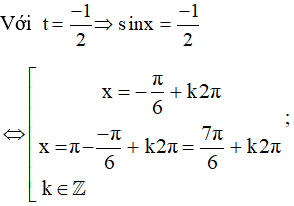
Vậy những nghiệm của phương trình đã cho là
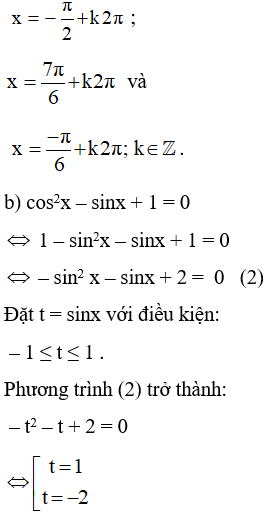
Trong hai nghiệm thì chỉ có nghiệm t = 1 thỏa mãn nhu cầu .
Với t = 1 thì sinx = 1 ⇔ x = π2 + k2π ; k ∈ ℤ .
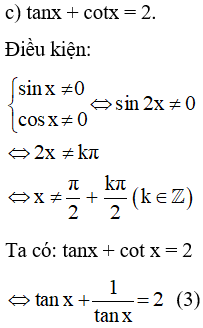
Đặt t = tan x ( với t ≠ 0 ), phương trình ( 3 ) trở thành :
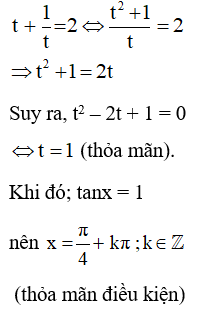
Bài 2. Giải các phương trình:
a ) 2 sin2 x + 2 sinx. cosx – 4 cos2x = 0 ;
b ) 3 sin2x + sin2x + 3 cos2x = 2 .
Lời giải:
a ) 2 sin2 x + 2 sinx. cosx – 4 cos2x = 0 ( 1 )
+ Nếu cosx = 0 thì sin2x = 1 nên phương trình ( 1 ) có :
VT ( 1 ) = 2 và VP ( 1 ) = 0
Suy ra, cos x = 0 không thỏa mãn nhu cầu phương trình ( 1 ). Vậy cosx ≠ 0 .
+ Vì cosx ≠ 0 nên chia hai vế của phương trình ( 1 ) cho cos2 x, ta được :
2 tan2x + 2 tanx – 4 = 0 ( 2 )
Đặt t = tanx, phương trình ( 2 ) trở thành : 2 t2 + 2 t – 4 = 0
⇔ t = 1 t = − 2
Với t = 1 thì tanx = 1 ⇔ x = π4 + kπ ; k ∈ ℤ .
Với t = – 2 thì tanx = – 2 ⇔ x = arctan − 2 + kπ ; k ∈ ℤ
Vậy phương trình đã cho có những nghiệm là
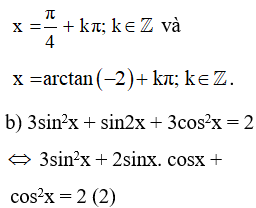
+ Nếu cosx = 0 thì sin2x = 1 nên phương trình ( 2 ) có :
VT ( 2 ) = 3 và VP ( 2 ) = 2
Suy ra, cos x = 0 không thỏa mãn nhu cầu phương trình ( 2 ). Vậy cosx ≠ 0 .
+ Vì cosx ≠ 0 nên chia hai vế của phương trình ( 2 ) cho cos2 x, ta được :
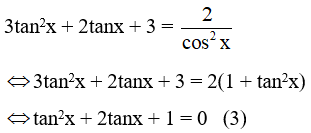
Đặt t = tanx, phương trình ( 3 ) trở thành :

Bài 3. Giải các phương trình sau:
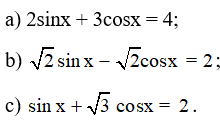
Lời giải:
a ) Ta có :
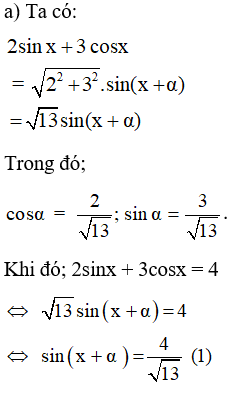
Vì 413 > 1 nên phương trình ( 1 ) vô nghiệm .
Vậy phương trình đã cho vô nghiệm .
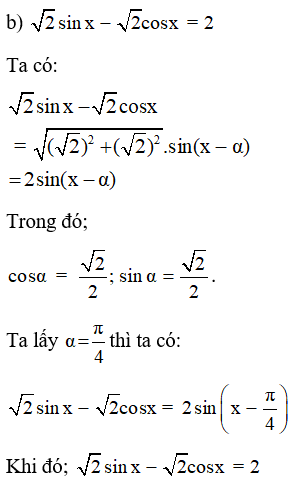

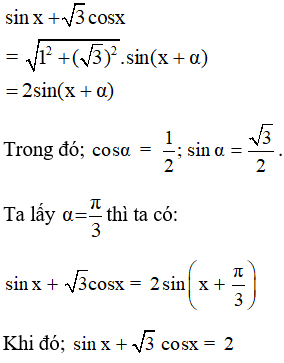

Bài 4. Giải phương trình:
sin2x − 3 cosx = sinx − 3 cos2x
Lời giải:
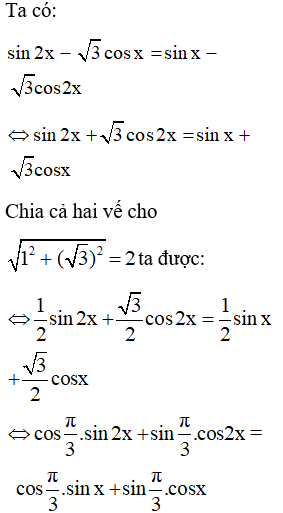
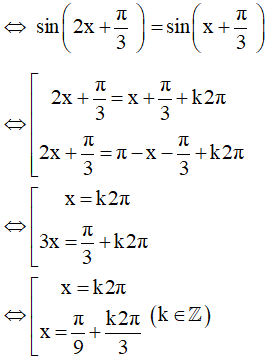
Vậy nghiệm của phương trình là
x=k2π; x=π9+k2π3 k∈ℤ
Xem thêm các bài tổng hợp lý thuyết Toán lớp 11 đầy đủ, chi tiết khác:
Lý thuyết Ôn tập chương 1
Lý thuyết Hoán vị – Chỉnh hợp – Tổ hợp
Lý thuyết Nhị thức Niu-tơn
Lý thuyết Phép thử và biến cố
Lý thuyết Xác suất của biến cố
Source: http://wp.ftn61.com
Category: Hỏi Đáp


Để lại một bình luận