Tóm tắt nội dung bài viết
- NHỊ THỨC NEWTON
- Định nghĩa về nhị thức newton
- Tính chất của công thức nhị thức Newton
- Một số kiến thức liên quan
- BÀI TOÁN VỀ NHỊ THỨC NEWTON
- Cách giải bài toán tìm số hạng thứ k trong khai triển nhị thức Newton
- Bài toán tìm hệ số trong khai triển nhị thức Newton.
- Bài toán tính tổng, chứng minh đẳng thức
- Phương pháp giải các bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp
- Bài toán về phương trình, bất phương trình chứa tổ hợp
- BÀI TẬP RÈN LUYỆN
NHỊ THỨC NEWTON
Định nghĩa về nhị thức newton
Nhị thức NewtonKhai triển ( a + b ) n được cho bởi công thức sau :Với a, b là những số thức và n là số nguyên dương, ta có :
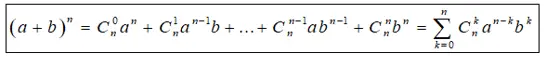
Bạn đang đọc: TÌM HIỂU VỀ NHỊ THỨC NEWTON
Quy ước a0 = b0 = 1Hệ quả :
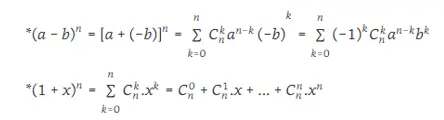
Tính chất của công thức nhị thức Newton
Tính chất của công thức nhị thức Newton
- Số các số hạng của công thức là n + 1
- Tổng số mũ của a và b trong mỗi số hạng luôn luôn bằng số mũ của nhị thức:
( n – k ) + k = n
- Số hạng tổng quát của nhị thức là:
Tk + 1 = Cnk an-k bk ( Đó là số hạng thứ k + 1 trong khai triển ( a + b ) n )
- Các hệ số nhị thức cách đều hai số hạng đầu, cuối thì bằng nhau

Một số kiến thức liên quan
Công thức khai triển nhị thức newton :
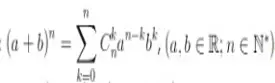
Công thức số tổng hợp
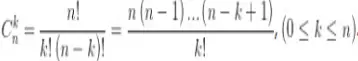
Tính chất lũy thừa
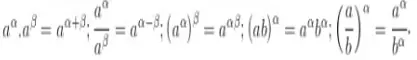
BÀI TOÁN VỀ NHỊ THỨC NEWTON
Cách giải bài toán tìm số hạng thứ k trong khai triển nhị thức Newton
Bước 1 : Khai triển nhị thức newton để tìm số hạng tổng quát :
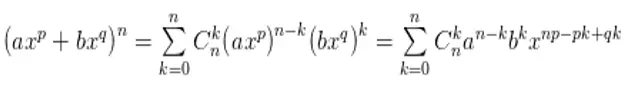
Bước 2 : Dựa vào đề bài, giải phương trình hai số mũ bằng nhauSố hạng chứa xm ứng với giá trị k thỏa : np – pk + qk = mTừ đó tìm : k = ( m – np ) / ( p – q )Vậy thông số của số hạng chứa xm là : Cnk an-k bk với giá trị k đã tìm được ở trênNếu k không gnhuyeen hoặc k > n thì trong khai triển không chứa xm, thông số phải tìm bằng 0Chú ý : Xác định thông số của số hạng chứa xm trong khai triểnP. ( x ) = ( a + bxp + cxq ) n được viết dưới dạng a0 + a1x + … + a2nx2nTa làm như sau :
- Viết P (x) = ( a + bxp + cxq)n
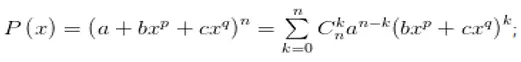
- Viết số hạng tổng quát khi khai triển các số hạng dạng bxp + cxq
- Thành một đa thức theo lũy thừa của x
- Từ số hạng tổng quát của hai khai triển trên ta tính được hệ số của xm
Chú ý : Để xác lập thông số lớn nhất trong khai triển nhị thức newtonTa làm như sau :
- Tính hệ số ak theo k và n
- Giải bất phương trình sau với ẩn số k
![]()
- Hệ số lớn nhất phải tìm ứng với số tự nhiên k lớn nhất thỏa mãn bất phương trình trên
Ví dụ 1 : Tìm số hạng thứ 21 trong khai triển ( 2 – 3 x ) 25GiảiSố hạng thứ 21 trong khai triển là :C2025. 25 ( – 3 x ) 20 = 25. 320. C2025. X20Ví dụ 2 : Tìm số hạng chính giữa trong khai triển ( 3×2 – y ) 10Giải :Trong khai triển ( 3×2 – y ) 10 có tổng thể 11 số hạng nên số hạng chính giữa là số hạng thứ 6. Vậy thông số của số hạng thứ 6 là – 35. C510Ví dụ 3 : Tìm thông số của x3, ( x > 0 ) trong khai triển sau :
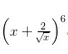
Giải :Số hạng tổng quát trong khai triển trên là : Tk + 1 = Ck6. x6-k. 2 k. x ( – k / 2 )Yêu cầu bài toán xảy ra khi 6 – k – ( k / 2 ) = 3 => k = 3Khi đó thông số của x3 là : C36. 23 = 160
Bài toán tìm hệ số trong khai triển nhị thức Newton.
Tìm thông số xk trong khai triển nhị thức newton
Phương pháp chung:
- Sử dụng công thức khai triển nhị thức newton
- Tìm số hạng có chứa xk và tìm hệ số tương ứng
Ví dụ : Tìm thông số của x3 trong khai triển ( 2 + x ) 5Giải :Ta có
![]()
Cho k = 3 ta được thông số của x3 là : C35. 25-3 = 40
Bài toán tính tổng, chứng minh đẳng thức
Phương pháp giải
- Sử dụng khai triển:
( a + b ) n = C0n an + C1n an-1b + C2n an-2b2 + … + Cn-1 n abn-1 + Cnn bnSuy ra điều phải chứng tỏ
- Bằng cách thay a, b, n bằng các giá trị thích hợp ta sẽ được các đẳng thức.
Bài toán ứng dụng nhị thức newton trong những bài tương quan đến tổng hợp
Phương pháp giải các bài toán ứng dụng nhị thức newton trong các bài liên quan đến tổ hợp
- Chọ một khai triển ( a+ x)n phù hợp, ở đây a là hằng số
- Sử dụng các phép biến đổi đại số hoặc lấy đạo hàm, tích phân
- Dựa vào điều kiện bài toán, thay x bởi một giá trị cụ thể
Bài toán về phương trình, bất phương trình chứa tổ hợp
Ví dụ : Giải bất phương trình sau : ( A22x – A2x < = ( 6 / x ). C3x + 10Giải :Điều kiện : x phải là 1 số ít nguyên dương và x > = 3Ta có bất phương trình đã cho tương tự với :
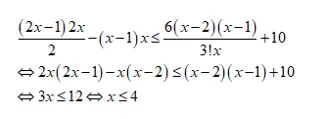
Vì x là nghiệm nguyên dương và x > = 3 nên x thuộc { 3 ; 4 }
BÀI TẬP RÈN LUYỆN
Bài tập 1: Tìm hệ số của x5 trong khai triển của biểu thức sau:
Xem thêm: Làm Thế Nào Để Học Giỏi Hóa 9?
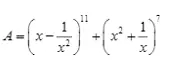
Giải :Công thức khai triển của biểu thức là :
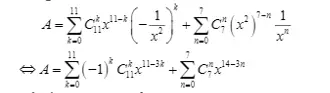
Để số hạng chứa x5 vậy k = 2 và n = 3Vậy thông số của x5 là C211 + C37 = 90Bài tập 2 : Tính B = 2 n C0n – 2 n – 1 C1n + 2 n – 2 C2n + … + ( – 1 ) k 2 n – k Ckn + … + ( – 1 ) 2 CnnGiải :
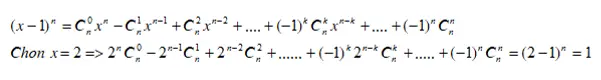
Bài tập 3 : Tính C = C610 + C710 + C810 + C910 + C1010Giải :
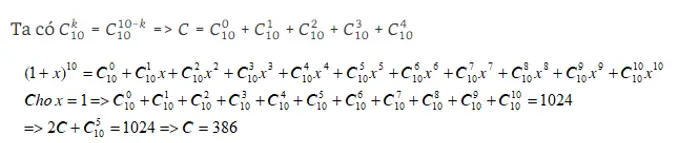
Bài tập 4 : Tìm thông số của x5 trong khai triển thành đa thức của biểu thức 😡 ( 1 – 2 x ) 5 + x2 ( 1 + 3 x ) 10Bài tập 5 : Với n là số nguyên dương, gọi a3n – 3 là thông số của x3n – 3 trong khai triển thành đa thức của ( x2 + 1 ) n ( x + 2 ) n. Tìm n để a3n – 3 = 26 nBài tập 6 : Tính tổng S = C02013 + 3 C12013 + 32 C22013 + … + 32013 C20132013
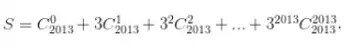
Bài tập 7 : Tìm thông số của số hạng chứa x10 trong khai triển biểu thức :
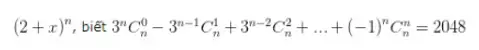
Bài tập 8 : Tìm ba số hạng tiên phong theo lũy thừa tăng dần của x trong khai triển ( 1 + 2 x ) 10Bài tập 9 : Tìm thông số của x5 trong khai triển P. ( x ) = ( x + 1 ) 6 + ( x + 1 ) 7 + … + ( x + 1 ) 12Bài tập 10 : Tìm thông số của số hạng thứ ba trong khai triển ( 2 a – b ) 5
Xem thêm: Làm Thế Nào Để Active Windows 7
Source: http://wp.ftn61.com
Category: Thủ Thuật



Để lại một bình luận