PHƯƠNG TRÌNH
1. Phương trình một ẩn:
– Một phương trình với ẩn x luôn có dạng A(x) = B(x), trong đó vế trái A(x) và vế phải B(x) là hai biểu thức của cùng một biến x.
Bạn đang đọc: Phương trình có vô số nghiệm là gì
Ví dụ 1.1. 2 x 3 = 5 ( x + 7 ) là phương trình với ẩn x .5 ( y + 6 ) = y2 + 26 là phương trình với ẩn y .- Nếu x0 là một giá trị sao cho A ( x0 ) = B ( x0 ) là một đẳng thức đúng thì x = x0 đgl một nghiệm của phương trình A ( x ) = B ( x ) .- Một phương trình hoàn toàn có thể có một nghiệm, hai nghiệm, ba nghiệm, có vô số nghiệm, nhưng cũng hoàn toàn có thể không nghiệm nào ( phương trình vô nghiệm )- Tập hợp toàn bộ những nghiệm của một phương trình đgl tập nghiệm của phương trình đó và thường được ký hiệu là S .- Đề giải một phương trình là đi tìm tổng thể những nghiệm của phương trình đó .Ví dụ 1.2 .* Phương trình x + 2 = 3 có tập nghiệm S = { 1 }* Phương trình ( x – 3 ) ( x2 – 4 ) = 0 có tập nghiệm S = { – 2 ; 2 ; 3 }
* Phương trình 0x = 1; x2 + 1 = 0; à các phương trình vô nghiệm và có tập nghiệm là S =
* Phương trình 0 x = 0 ; x2 1 = ( x 1 ) ( x + 1 ) có vô số nghiệm nên S = R- Số tập nghiệm của một phương trình còn phụ thuộc vào vào việc xét những giá trị của ẩn trên tập hợp số nào .Ví dụ 1.3 .Xét phương trình ( 3 x 4 ) ( x2 3 ) = 0 sẽ vô nghiệm trên tập N, ZXét phương trình ( 3 x 4 ) ( x2 3 ) = 0 có một nghiệm ( x = 4/3 ) trên tập Q.
Xét phương trình (3x 4)(x2 3) = 0 có ba nghiệm (x = 4/3, x = ) trên tập R.
2. Hai phương trình tương đương:
2.1. Định nghĩa: Hai phương trình gọi là tương đương nếu chúng có cùng một tập hợp nghiệm.
* Sự tương đương ký hiệu bởi dấu . Phương trình (1) tương đương với phương trình (2), ta viết (1)
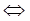(2)
* Hai phương trình vô nghiệm được coi là tương tự
Ví dụ 2.1. Xét 2 phương trình x2 + 1 = 0 và phương trình 0x = -3 là hai phương trình tương đương nhau vì có cùng tập nghiệm chúng bằng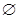 
.
3 bí quyết giải toán phương trình cực đỉnh
2.2. Hai quy tắc biến đổi tương đương các phương trình:
2.2.1. Quy tắc chuyển vế : ( SGK )
A ( x ) = B ( x ) + C ( x ) A ( x ) C ( x ) = B ( x )2.2.2. Quy tắc nhân ( chia ) với một số ít :
A(x) = B(x) m.A(x) = m.B(x) (m R*)
3. Phương trình bậc nhất một ẩn:
3.1. Định nghĩa: Phương trình dạng ax + b = 0 với a, b là những hằng số; a 0 đgl phương trình bậc nhất một ẩn.
Ví dụ 3.1. 2 x 1 = 0 ; 4 y + 6 = 0 ; 2 5 t = 0 ; 3 z = 0 ; là những phương trình bậc nhất một ẩn .Ví dụ 3.2. x ( x 1 ) = 0 ; 0 x + 2 = 0 ; không phải những phương trình bậc nhất một ẩn .
3.2. Cách giải: ax + b = 0 ax = – b
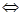x = -b/a
Nghiệm duy nhất của phương trình ax + b = 0 (a 
0) là x = -b/a
4. Cách giải phương trình đưa được về dạng ax + b = 0 (a0) (khôngcó ẩn ở mẫu):
– Quy đồng mẫu thức 2 vế- Khử mẫu thức .- Thực hiện những phép tính và chuyển vế ( chuyển những hạng tử chứa ẩn sang một vế, những hằng số sang vế bên kia ), đưa phương trình về dạng Ax = B
Ví dụ 4.1. Giải phương trình:
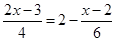
Vậy: S =
10 tuyệt chiêu giúp học giỏi Toán
Xem thêm: Bộ Kế hoạch Đầu tư Tiếng Anh là gì?
Source: http://wp.ftn61.com
Category: Hỏi Đáp
Từ khóa tìm kiếm: phương trình có thiếu gì nghiệm khi nào,khi nào phương trình có vô số nghiệm,pt có ti tỉ nghiệm khi nào,vô số nghiệm ký hiệu là gì,0=0 là vô nghiệm hay thiếu gì nghiệm,vô số nghiệm là gì,phương trình có vô số nghiệm là gì,vô số nghiệm tiếng anh,tập nghiệm là gì,3x 4,khoa thẩm mỹ đại học y dược
Nội dung khác
Toán học là môn khoa học đề cập đến logic của con số, cấu trúc, không gian và các phép biến đổi. Toán học có trong mọi thứ bao quanh chúng ta. Trong tất cả mọi thứ chúng ta làm. Đấy là thước đo cho mọi thứ trong cuộc sống hàng ngày.
Tính diễn ra từ khoa thẩm mỹ đại học y dược lịch sử khởi đầu được ghi lại, phát hiện Toán học đã đi tập nghiệm là gì đầu trong mọi xã hội tiến bộ. Là môn được sử dụng ngay vô số nghiệm tiếng anh cả trong những nền văn hóa nguyên thủy nhất. Nhu 0=0 là vô nghiệm hay vô số nghiệm cầu của Toán học sinh vô số nghiệm ký hiệu là gì ra dựa trên mong muốn của xã hội. Xã hội càng phát triển, nhu cầu tính toán phức tạp hơn. Các bộ tộc nguyên thủy ít dùng toán học mà đểtính toán địa điểm của mặt trời và vật lý săn bắn vẫn phải dựa vào Toán học.
Toán học là 1 ngành, 1 môn học pt có vô số nghiệm khi nào yêu cầu suy luận và trí khi nào phương trình có vô số nghiệm sáng dạ cao. Nó chứa tất cả phương trình có vô số nghiệm khi nào những gì thử thách tới bộ não của chúng ta. Học toán hay nghiên cứu Toán học là vận dụng khả năng suy luận và trí óc thông minh của chúng ta.
Môn Toán học là nền móng cho tất cả các cấp khoa học thiên nhiên khác. Có thể nói rằng ko có toán học, sẽ không có ngành khoa học nào cả.
Toán được phần mềm nhiều trong cuộc sống
Lịch sử ra đời của môn Toán học
Số đếm được có mặt trên thị trường đầu tiên
Sự có mặt trên thị trường và tăng trưởng của Toán có sự đóng góp của các nền tiến bộ ở Sume, Trung Quốc, Ấn Độ, người nào Cập, Trung Mỹ…. Người Sumer là những người trước nhất tăng trưởng một hệ thống đếm. Sumer là 1 nền văn minh cổ tăng trưởng rực rỡ vào thời đoạn bốn.000 5 TCN. Đây là 1 vùng lịch sử ở phía nam Lưỡng Hà, tức là Iraq ngày nay.
Các nhà toán học đã phát triển số học, bao gồm các phép toán cơ bản, phép nhân, phân số. Hệ thống đếm của người Sumer đã vượt qua Đế quốc Akkadian của người Babylon khoảng 300 năm. Ở Mỹ, người Mayans đã phát triển các hệ thống lịch phức tạp. Họ cũng là những nhà thiên văn học lành nghề. Khoảng thời kì này, định nghĩa về số ko đã được tăng trưởng.
Để lại một bình luận