Phương trình mặt cầu và các dạng bài tập có lời giải từ A – Z

Phương trình mặt cầu là kiến thức và kỹ năng cơ bản của khối lớp 12 nhưng lại có rất nhiều dạng bài tập trong những kỳ thi tốt nghiệp trung học phổ thông và ĐH lúc bấy giờ. Chính thế cho nên, trong bài viết dưới đây chúng tôi sẽ san sẻ kim chỉ nan và những dạng phương trình mặt cầu thường gặp để những bạn cùng tìm hiểu thêm nhé

Mặt cầu là gì?

Trong khoảng trống, mặt cầu là quỹ tích những điểm cách đều một điểm cho trước một khoảng chừng không đổi. Khoảng không đổi đó gọi là nửa đường kính. Điểm cho trước gọi là tâm mặt cầu .

Các dạng phương trình mặt cầu

1. Phương trình chính tắc

Trong khoảng trống Oxyz cho mặt cầu S tâm I ( a ; b ; c ) nửa đường kính R. Phương trình chính tắc của ( S ) là :

(x – a)2 + (y – b)2 + (z – c)2 = R2

2. Phương trình tổng quát

Nếu a2 + b2 + c2 – d > 0 thì phương trình sau đây là phương trình tổng quát của ( S ) :

x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 (1)

Tọa độ tâm của ( S ) có phương trình ( 1 ) là I ( a ; b ; c ) và nửa đường kính của ( S ) được tính theo công thức :

R = √a2 + b2 + c2 – d

Vị trí tương đối giữa mặt phẳng và mặt cầu.

Cho mặt cầu ( S ) : ( x − a ) 2 + ( b − y ) 2 + ( c − z ) 2 = R2 có tâm I, nửa đường kính R và mặt phẳng ( P ) : Ax + By + Cz + D = 0 .
Ta có :

• d(I,(P)) > R : Mặt phẳng (P) không cắt mặt cầu (S).
• d(I,(P)) = R : Mặt phẳng (P) tiếp xúc với mặt cầu (S).
• d(I,(P)) < R : Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn có tâm K là hình chiếu của I trên (P) và bán kính r=√R2−d2(I,(P))

Vị trí tương đối giữa đường thẳng và mặt cầu.

Cho mặt cầu ( S ) : ( x − a ) 2 + ( b − y ) 2 + ( c − z ) 2 = R2 có tâm I, nửa đường kính R và đường thẳng Δ
Ta có khoảng cách d từ mặt cầu ( S ) đến đường thẳng Δ :

• d > R: Đường thẳng Δ không cắt mặt cầu (S)
• d = R: Đường thẳng Δ tiếp xúc với mặt cầu (S)
• d < R: Đường thẳng Δ cắt mặt cầu (S) theo dây cung AB = √R2 – d2

Tham khảo thêm:

Các dạng bài tập viết phương trình mặt cầu thường gặp

Dạng 1: Xác định tâm và bán kính mặt cầu. Tìm điều kiện để phương trình dạng khai triển là phương trình của một đường tròn

Phương pháp :
Xét phương trình ( S ) : ( x − a ) 2 + ( b − y ) 2 + ( c − z ) 2 = R2. Khi đó mặt cầu có tâm I ( a ; b ; c ), nửa đường kính R
Xét phương trình ( S ) : x2 + y2 + z2 – 2 ax – 2 by – 2 cz + d = 0 .
Điểu kiện để phương trình trên là phương trình mặt cầu là : a2 + b2 + c2 – d > 0
Khi đó ( S ) có tâm I ( a ; b ; c ) và bán kínhR = √ a2 + b2 + c2 – d
Ví dụ 1 :
Trong khoảng trống với hệ tọa độ Oxyz, cho mặt cầu ( S ) có phương trình : x2 + y2 + z2 + 2 x – 4 y + 6 z – 2 = 0. Tính tọa độ tâm I và nửa đường kính R của ( S ) .
Lời giải :
Phương trình ( S ) : x2 + y2 + z2 + 2 x – 4 y + 6 z – 2 = 0 có :
Tâm I ( – 1, 2, 3 )

R = √a2 + b2 + c2 – d = √(-1)2 + (2)2 + (3)2 – (-2) = √16 = 4

Dạng 2: Viết phương trình mặt cầu biết tâm và bán kính

Dạng 3: Viết phương trình mặt cầu (S) có đường kính AB cho trước

Phương pháp :

• Tìm trung điểm của AB. Vì AB là đường kính nên I là tâm trung điểm AB đồng thời là tâm của mặt cầu.
• Tính độ dài IA = R.
• Làm tiếp như bài toán dạng 1.

Ví dụ : Cho hai điểm A ( – 2 ; 1 ; 0 ) và B ( 2 ; 3 ; – 2 ). Phương trình mặt cầu đường kính AB là :
A. ( x + 2 ) 2 + ( y – 1 ) 2 + ( z + 1 ) 2 = 8 ; B. x2 + ( y + 2 ) 2 + ( z – 1 ) 2 = 10
C. x2 + ( y – 2 ) 2 + ( z + 1 ) 2 = 6 ; D. ( x – 2 ) 2 + ( y + 1 ) 2 + ( z – 1 ) 2 = 8
Lơi giải :
Gọi M là trung điểm của AB, tọa độ điểm M là :

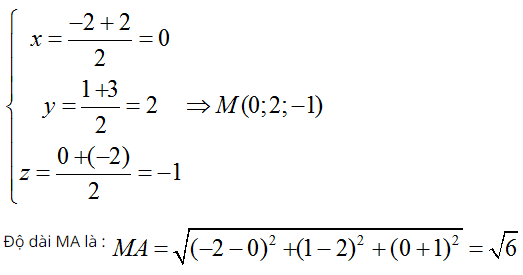
Mặt cầu cần tìm nhận M ( 0 ; 2 ; – 1 ) làm tâm và có nửa đường kính là R = MA = √ 6 .
Ta có phương trình mặt cầu là : ( x – 0 ) 2 + ( y – 2 ) 2 + ( z + 1 ) 2 = 6 Hay x2 + ( y – 2 ) 2 + ( z + 1 ) 2 = 6

Dạng 4: Viết mặt cầu (S) qua 3 điểm A, B, C và có tâm thuộc mặt phẳng (P) cho trước.

Cách 1 :

• Bước 1: Gọi phương trình mặt cầu là x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 ( *) (với a2 + b2 + c2 – d > 0 )
• Bước 2: Thay tọa độ bốn điểm A, B, C, D vào phương trình (*), ta được hệ 4 phương trình.
• Bước 3: Giải hệ trên tìm được a, b, c, d( chú ý đối chiếu điều kiện a2 + b2 + c2 – d > 0 ). Thay a, b, c, d vào (*) ta được phương trình mặt cầu cần lập.

Cách 2 :

Bước 1: Gọi I(a, b, c) là tâm mặt cầu đi qua bốn điểm A, B, C, D. Suy ra: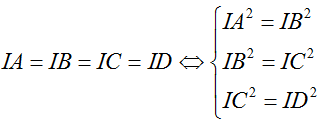

Bước 2 : Giải hệ trên để tìm a, b, c .
Bước 3 : Tìm nửa đường kính R = IA. Từ đó, viết phương trình mặt cầu cần tìm có dạng ( x – a ) 2 + ( y – b ) 2 + ( z – c ) 2 = R2
Ví dụ : Nếu mặt cầu ( S ) đi qua bốn điểm M ( 2 ; 2 ; 2 ) ; N ( 4 ; 0 ; 2 ) ; P ( 4 ; 2 ; 0 ) và Q. ( 4 ; 2 ; 2 ) thì tâm I của ( S ) có toạ độ là :
A. ( – 1 ; – 1 ; 0 ) B. ( 3 ; 1 ; 1 ) C. ( 1 ; 1 ; 1 ) D. ( 1 ; 2 ; 1 )
Hướng dẫn giải :
Gọi phương trình mặt cầu ( S ) : x2 + y2 + z2 – 2 ax – 2 by – 2 cz + d = 0 ( a2 + b2 + c2 – d > 0 ) .
Do M ( 2 ; 2 ; 2 ) ∈ ( S ) 22 + 22 + 22 – 2.2 a – 2.2 b – 2.2 c + d = 0 hay – 4 a – 4 b – 4 c + d = – 12 ( 1 )
Do N ( 4 ; 0 ; 2 ) ∈ ( S ) nên 42 + 02 + 22 – 2.4 a – 2.0 b – 2.2 c + d = 0 hay – 8 a – 4 c + d = – 20 ( 2 )
Do P ( 4 ; 2 ; 0 ) ∈ ( S ) nên 42 + 22 + 02 – 2.4 a – 2.2 b – 2.0. c + d = 0 hay – 8 a – 4 b + d = – 20 ( 3 )

Do Q(4; 2; 2) ∈ (S) nên 42 + 22 + 22 – 2.4 a -2.2b – 2.2c + d = 0 hay – 8a – 4b – 4c + d = -24 (4)

Từ ( 1 ) ; ( 2 ) ; ( 3 ) và ( 4 ) ta có hệ phương trình :

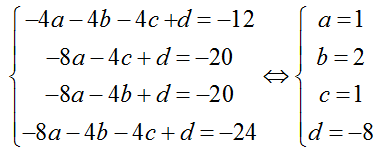
Suy ra, mặt cầu ( S ) thỏa mãn nhu cầu có tâm I ( 1 ; 2 ; 1 ). Chọn đáp án A

Dạng 5: Viết phương trình mặt cầu có tâm I, một đường thẳng ( mặt phẳng) cắt mặt cầu thỏa mãn điều kiện T.

Phương pháp :
Phương trình mặt cầu ( S ) biết tâm I và cắt đường thẳng d theo dây cung AB :

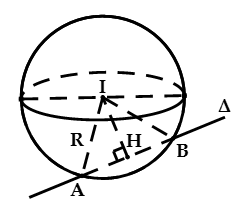
• Bước 1: Tính khoảng cách từ tâm I đến đường thẳng d
• Bước 2: Dựa vào giả thuyết đề cho, ta tính độ dài dây cung AB. Suy ra độ dài AH (với H là trung điểm AB)
• Bước 3: Tính IA theo định lý Pitago cho tam giác vuông AIH. Suy ra bán kính R= IA.

Phương trình mặt cầu ( S ) biết tâm I và cắt mặt phẳng ( P ) theo đường tròn giao tuyến ( C )

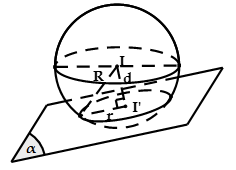
Bước 1 : Tính khoảng cách từ tâm I đến mặt phẳng ( P )
Bước 2 : Dựa vào giả thuyết đề cho, ta tính nửa đường kính r của đường tròn giao tuyến. Suy ra nửa đường kính mặt cầu R = √ d2 ( I, ( P ) ) + R2

Do đó, phương trình mặt cầu là : ( x – 2 ) 2 + ( y – 3 ) 2 + ( z + 1 ) 2 = 76
( S ) : ( x – 2 ) 2 + ( y – 3 ) 2 + ( z + 1 ) 2 = 76 .
Chọn A .

Dạng 6: Lập phương trình mặt cầu tiếp xúc với đường thẳng, mặt phẳng và thỏa mãn điều kiện T

1. Ví dụ minh họa
Ví dụ 1 : Cho điểm A ( 2 ; 5 ; 1 ) và mặt phẳng ( P ) : 6 x + 3 y – 2 z + 24 = 0, H là hình chiếu vuông góc của A trên mặt phẳng ( P ). Phương trình mặt cầu ( S ) có diện tích quy hoạnh và tiếp xúc với mặt phẳng ( P ) tại H, sao cho điểm A nằm trong mặt cầu là :
A. ( x – 8 ) 2 + ( y – 8 ) 2 + ( z + 1 ) 2 = 196 B. ( x + 82 + ( y + 8 ) 2 + ( z – 1 ) 2 = 196
C. ( x + 16 ) 2 + ( y + 4 ) 2 + ( z – 7 ) 2 = 196 D. ( x – 16 ) 2 + ( y – 4 ) 2 + ( z + 7 ) 2 = 196
Hướng dẫn giải :
Gọi d là đường thẳng đi qua A và vuông góc với ( P ). Suy ra, một VTCP của d là :

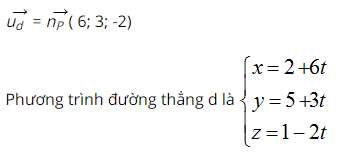
Vì H là hình chiếu vuông góc của A trên ( P ) nên H = d ∩ ( P ) .
Vì H ∈ d nên H ( 2 + 6 t ; 5 + 3 t ; 1 – 2 t .
Mặt khác, H ∈ ( P ) nên ta có :
6 ( 2 + 6 t ) + 3 ( 5 + 3 t ) – 2 ( 1 – 2 t ) + 24 = 0
⇔ t = – 1
Do đó, H ( – 4 ; 2 ; 3 ) .
Gọi I và R lần lượt là tâm và nửa đường kính mặt cầu .
Theo giả thiết diện tích quy hoạnh mặt cầu bằng 784 π, suy ra 4 πR2 ⇔ R = 14 .
Vì mặt cầu tiếp xúc với mặt phẳng ( P ) tại H nên IH ⊥ ( P ) => I ∈ d .
Do đó tọa độ điểm I có dạng I ( 2 + 6 t ; 5 + 3 t ; 1 – 2 t ), với t ≠ – 1 .
Theo giả thiết, tọa độ điểm I thỏa mãn nhu cầu :

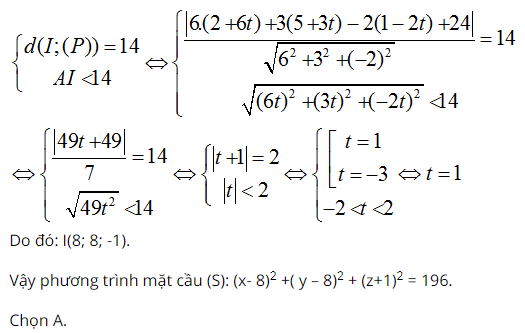
Sau khi đọc xong bài viết của chúng tôi những bạn hoàn toàn có thể nắm được những dạng phương trình mặt cầu từ đó vận dụng vào làm bài tập nhé

Đánh giá bài viết

Source: http://wp.ftn61.com
Category: Thủ Thuật