Sách Giải Bài Tập Toán Lớp 8 Bài 2: Phương Trình Bậc Nhất Một Ẩn Và Cách Giải

Xem toàn bộ tài liệu Lớp 8: tại đây

Xem thêm các sách tham khảo liên quan:

Sách giải toán 8 Bài 2 : Phương trình bậc nhất một ẩn và cách giải giúp bạn giải những bài tập trong sách giáo khoa toán, học tốt toán 8 sẽ giúp bạn rèn luyện năng lực suy luận hài hòa và hợp lý và hợp logic, hình thành năng lực vận dụng kết thức toán học vào đời sống và vào những môn học khác :

Trả lời câu hỏi Toán 8 Tập 2 Bài 2 trang 8: Giải các phương trình:

a) x – 4 = 0;

b ) 3/4 + x = 0 ;
c ) 0,5 – x = 0 .

Lời giải

a ) x – 4 = 0
⇔ x = 0 + 4
⇔ x = 4
Vậy phương trình có một nghiệm duy nhất x = 4
b ) 3/4 + x = 0
⇔ x = 0-3 / 4
⇔ x = – 3/4
Vậy phương trình có một nghiệm duy nhất x = – 3/4
c ) 0,5 – x = 0
⇔ x = 0,5 – 0
⇔ x = 0,5
Vậy phương trình có một nghiệm duy nhất x = 0,5

Trả lời câu hỏi Toán 8 Tập 2 Bài 2 trang 8: Giải các phương trình:

a ) x / 2 = – 1 ;
b ) 0,1 x = 1,5 ;
c ) – 2,5 x = 10 .

Lời giải

a ) x / 2 = – 1
⇔ x = ( – 1 ). 2
⇔ x = – 2
Vậy phương trình có một nghiệm duy nhất x = – 2
b ) 0,1 x = 1,5
⇔ x = 1,5 / 0,1
⇔ x = 15
Vậy phương trình có một nghiệm duy nhất x = 15
c ) – 2,5 x = 10
⇔ x = 10 / ( – 2,5 )
⇔ x = – 4
Vậy phương trình có một nghiệm duy nhất x = – 4

Trả lời câu hỏi Toán 8 Tập 2 Bài 2 trang 9: Giải phương trình: -0,5x + 2,4 = 0.

Lời giải

– 0,5 x + 2,4 = 0
⇔ – 0,5 x = – 2,4
⇔ x = ( – 2,4 ) / ( – 0.5 )
⇔ x = 4,8
Vậy phương trình có một nghiệm duy nhất x = 4,8

Bài 2: Phương trình bậc nhất một ẩn và cách giải

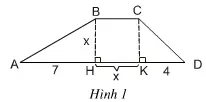
Bài 6 (trang 9 SGK Toán 8 tập 2): Tính diện tích S của hình thang ABCD theo x bằng hai cách:

1 ) Tính theo công thức : S = BH x ( BC + DA ) : 2
2 ) S = SABH + SBCKH + SCKD
Sau đó, sử dụng giả thiết S = 20 để thu được hai phương trình tương tự với nhau. Trong hai phương trình ấy, có phương trình nào là phương trình bậc nhất không ?

Lời giải:

1 ) Ta có : S = BH x ( BC + DA ) : 2
+ BCKH là hình chữ nhật nên BC = KH = x
+ BH = x
+ AD = AH + HK + LD = 7 + x + 4 = 11 + x .
Vậy S = BH x ( BC + DA ) : 2 = x. ( x + 11 + x ) : 2 = x. ( 2 x + 11 ) : 2 .
2 ) S = SABH + SBCKH + SCKD

+ ABH là tam giác vuông tại H

⇒ SBAH = 50%. BH.AH = 50%. 7. x = 7 x / 2 .
+ BCKH là hình chữ nhật
⇒ SBCKH = x. x = x2 .
+ CKD là tam giác vuông tại K
⇒ SCKD = 50%. CK.KD = 50%. 4. x = 2 x .
Do đó : S = SABH + SBCKH + SCKD = 7 x / 2 + x2 + 2 x = x2 + 11 x / 2 .
– Với S = 20 ta có phương trình

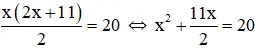
Trong hai phương trình này, không có phương trình nào là phương trình bậc nhất .

Bài 2: Phương trình bậc nhất một ẩn và cách giải

Bài 7 (trang 10 SGK Toán 8 tập 2): Hãy chỉ ra các phương trình bậc nhất trong các phương trình sau:

a ) 1 + x = 0

b ) x + x2 = 0
c ) 1 – 2 t = 0
d ) 3 y = 0
e ) 0 x – 3 = 0 .

Lời giải:

+ Phương trình 1 + x = 0 là phương trình bậc nhất với a = 1 ; b = 1 .
+ Phương trình x + x2 không phải phương trình bậc nhất vì có chứa x2 bậc hai .
+ Phương trình 1 – 2 t = 0 là phương trình bậc nhất ẩn t với a = – 2 và b = 1 .
+ Phương trình 3 y = 0 là phương trình bậc nhất ẩn y với a = 3 và b = 0 .
+ Phương trình 0 x – 3 = 0 không phải phương trình bậc nhất vì thông số bậc nhất a = 0 .

Bài 2: Phương trình bậc nhất một ẩn và cách giải

Bài 8 (trang 10 SGK Toán 8 tập 2): Giải các phương trình:

a ) 4 x – 20 = 0
b ) 2 x + x + 12 = 0
c ) x – 5 = 3 – x
d ) 7 – 3 x = 9 – x

Lời giải:

a ) 4 x – 20 = 0
⇔ 4 x = 20
⇔ x = 5
Vậy phương trình có nghiệm duy nhất x = 5 .
b ) 2 x + x + 12 = 0
⇔ 3 x + 12 = 0
⇔ 3 x = – 12
⇔ x = – 4
Vậy phương trình đã cho có nghiệm duy nhất x = – 4
c ) x – 5 = 3 – x
⇔ x + x = 5 + 3
⇔ 2 x = 8
⇔ x = 4
Vậy phương trình có nghiệm duy nhất x = 4
d ) 7 – 3 x = 9 – x
⇔ 7 – 9 = 3 x – x
⇔ – 2 = 2 x
⇔ x = – 1
Vậy phương trình có nghiệm duy nhất x = – 1 .

Bài 2: Phương trình bậc nhất một ẩn và cách giải

Bài 9 (trang 10 SGK Toán 8 tập 2): Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.

a ) 3 x – 11 = 0
b ) 12 + 7 x = 0

c) 10 – 4x = 2x – 3

Lời giải:

Source: http://wp.ftn61.com
Category: Hỏi Đáp