Đề bài
BÁO CÁO THỰC HÀNH:
Khảo sát chuyển động rơi tự do. Xác định gia tốc rơi tự do
Lời giải chi tiết
1. Trả lời câu hỏi: Sự rơi tự do là gì ? Nếu đặc điểm của chuyển động rơi tự do và viết công thức tính gia tốc rơi tự do ?
– Sự rơi tự do là sự rơi chỉ dưới tính năng của trọng tải .- Đặc điểm :+ Phương thẳng đứng, chiều từ trên xuống .+ Là chuyển động nhanh dần đều .+ Tại một nơi nhất định trên Trái Đất và ở gần mặt đất, mọi vật đều rơi tự do với cùng tần suất g .- Công thức tính tần suất rơi tự do : \ ( g = \ dfrac { 2 s } { t } \ )Trong đó :+ s : quãng đường đi được của vật rơi tự do ( m ) .+ t : thời hạn vật rơi tự do ( s ) .
2. Kết quả
Bảng 8.1 Khảo sát chuyển động rơi tự do : Đo thời gian rơi ứng với các khoảng cách s khác nhau.
Vị trí đầu của vật rơi : \ ( s_0 = 0 ( mm ) \ ) .

Trong đó : \ ( \ overline { { t_i } } = \ dfrac { { { t_1 } + { t_2 } + .. + { t_5 } } } { 5 } \ )
Vẽ đồ thị: Dựa vào kết quả trong Bảng 8.1, chọn tỉ lệ thích hợp trên các trục tung và trục hoành để vẽ đồ thị \(s = s(t^2)\).
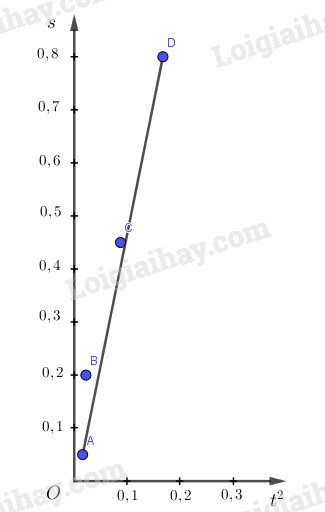
Xem thêm: Làm Thế Nào Để Win 7 Chạy Nhanh Hơn
a ) Nhật xét :Ta có : \ ( s = \ dfrac { gt ^ 2 } { 2 } = s ( t ) \ ) .Như vậy s nhờ vào vào thời hạn là hàm bậc 2 ẩn t, do vậy nếu vẽ đồ thị trình diễn s qua t thì nó có dạng một đường cong Parabol .Nhưng bài toán hỏi dạng đồ thị của s theo ẩn \ ( ( t ^ 2 ) \ ), do vậy tất cả chúng ta phải chú ý quan tâm .Từ \ ( s = \ dfrac { gt ^ 2 } { 2 } \ to s = \ dfrac { g. X } { 2 } \ ) với \ ( X = t ^ 2 \ ), ở đây t là biến nên X cũng là biến .Ta nhận thấy sự phụ thuộc vào của s theo ẩn X là một hàm số bậc nhất :\ ( Y = A.X + B \ ) ( với \ ( A = g / 2, B = 0 \ ) ) nên đồ thị \ ( s = s ( t ^ 2 ) = s ( X ) \ ) có dạng là một đường thẳng .Như vậy chuyển động của vật rơi tự do là chuyển động thẳng nhanh dần đều .b ) Khi đã xác lập được chuyển động rơi tự do là một chuyển động nhanh dần đều, ta hoàn toàn có thể xác lập những giá trị của g theo công thức \ ( g = \ dfrac { 2 s } { t ^ 2 } \ ) và tốc độ của vật rơi tại cổng E theo công thức \ ( v = \ dfrac { 2 s } { t } \ ) ứng với mỗi lần đo. Hãy tính những giá trị trên và ghi vào bảng 8.1
c) Đồ thị \(v = v(t)\) có dạng một đường thẳng, tức là vận tốc rơi tự do tăng dần theo thời gian. Vậy chuyển động rơi tự do là chuyển động thẳng nhanh dần đều
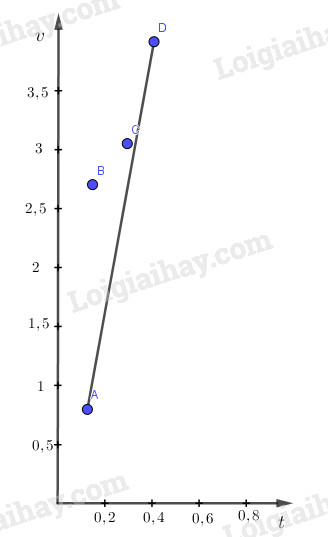
d )Ta có :\ ( \ begin { array } { l } \ overline g = \ dfrac { { { g_1 } + { g_2 } + { g_3 } + { g_4 } } } { 4 } \ \ = \ dfrac { { 6,339 + 18,261 + 10,342 + 9,583 } } { 4 } \ \ = 11,13 m / { s ^ 2 } \ end { array } \ )
\(\begin{array}{l}\Delta {g_1} = \left| {\overline g – {g_1}} \right| = 4,791\\\Delta {g_2} = \left| {\overline g – {g_2}} \right| = 7,131\\\Delta {g_3} = \left| {\overline g – {g_3}} \right| = 0,788\\\Delta {g_4} = \left| {\overline g – {g_4}} \right| = 1,547\end{array}\)
Xem thêm: làm thế nào để iphone 6 không bị đơ
e )Kết quả : \ ( g = \ overline g \ pm { \ left ( { \ Delta g } \ right ) _ { max } } = 11,13 \ pm 7,131 \ left ( { m / { s ^ 2 } } \ right ) \ )
Loigiaihay.com
Source: http://wp.ftn61.com
Category: Thủ Thuật



Để lại một bình luận