Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ

1. Góc giữa hai vectơ

Cho hai vectơ \ ( \ vec a \ ) và \ ( \ vec b \ ). Từ điểm 0 bất kể, dựng \ ( \ vec OA \ ) = \ ( \ vec a \ ). \ ( \ vec OB \ ) = \ ( \ vec b \ ) .

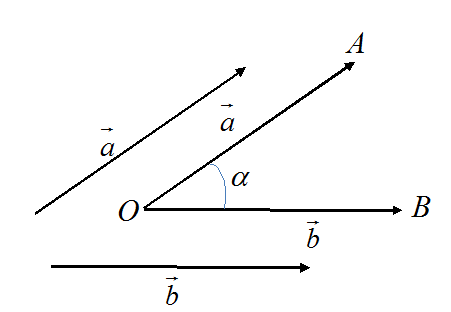
Khi đó : số đo USD \ widehat { AOB } = \ alpha USD gọi là số đo của góc giữa hai vectơ \ ( \ vec a \ ) và \ ( \ vec b \ ) .
Đặc biệt : Nếu USD \ widehat { AOB } = \ alpha = { 90 ^ 0 } USD, ta nói \ ( \ vec a \ ) vuông góc với \ ( \ vec b \ ), kí hiệu : USD \ overrightarrow a \ bot \ overrightarrow b USD .

2. Định nghĩa tích vô hướng của hai vectơ

Định nghĩa: Tích vô hướng của hai vectơ \(\vec a\) và \(\vec b\) là một số , được kí hiệu là \(\vec a.\vec b\) và được xác định bởi công thức:

\ ( \ vec a. \ vec b = | \ vec a |. | \ vec b |. cos \ left ( \ vec a, \ vec b \ right ) \ )

3. Tính chất của tích vô hướng

a) Định lí

Với ba vectơ \ ( \ vec a, \ vec b, \ vec c \ ) tùy ý và 1 số ít thực k, ta có :
+ \ ( \ vec a. \ vec b = \ vec b. \ vec a \ ) ( đặc thù giao hoán )
+ \ ( \ vec a. \ vec b = 0 \ Leftrightarrow \ vec a \ perp \ vec b \ )
+ \ ( ( k \ vec a ). \ vec b = \ vec a. ( k \ vec b ) = k. ( \ vec a. \ vec b ) \ )
+ \ ( \ vec a. ( \ vec b \ pm \ vec c ) = \ vec a. \ vec b \ pm \ vec a. \ vec c \ ) ( đặc thù phân phối )

b) Hệ quả

Hệ quả 1: Bình phương vô hướng

Với mỗi vectơ \ ( \ vec a \ ) tùy ý, tích vô hướng \ ( \ vec a. \ vec a \ ) được kí hiệu là \ ( | \ vec a | ^ 2 \ ) được gọi là bình phương vô hướng .
Ta có : \ ( \ vec a ^ 2 = | \ vec a |. | \ vec a |. cos0 ^ o = | \ vec a | ^ 2 \ )

Như vậy: Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.

Hệ quả 2: Hằng đẳng thức véc tơ

$\begin{array}{l}
+ {{\vec a}^2} \ge 0;{{\vec a}^2} = 0 \Leftrightarrow \vec a = \vec 0\\
+ {\left( {\vec a + \vec b} \right)^2} = {{\vec a}^2} + 2\vec a.\vec b + {{\vec b}^2}\\
+ {\left( {\vec a – \vec b} \right)^2} = {{\vec a}^2} – 2\vec a.\vec b + {{\vec b}^2}\\
+ {{\vec a}^2} – {{\vec b}^2} = \left( {\vec a – \vec b} \right)\left( {\vec a + \vec b} \right)
\end{array}$

Hệ quả 3. Dấu của tích vô hướng

USD + \ vec a. \ vec b > 0 \ Leftrightarrow 0 ^ 0 < \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) < { 90 ^ 0 } USD USD + \ vec a. \ vec b < 0 \ Leftrightarrow { 90 ^ 0 } < \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) < { 180 ^ 0 } USD Chứng minh : Ta có : USD \ vec a. \ vec b = \ left | { \ overrightarrow a } \ right |. \ left | { \ overrightarrow b } \ right | \ cos \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) USD . Do : USD \ left | { \ overrightarrow a } \ right | > 0 ; \ left | { \ overrightarrow b } \ right | > 0 USD
nên : USD \ vec a. \ vec b > 0 \ Leftrightarrow \ cos \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) > 0 USD
USD \ Leftrightarrow { 0 ^ 0 } < \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) < { 90 ^ 0 } USD . Góc USD \ left ( { \ vec a, \ vec b } \ right ) USD nhọn . Tương tự : USD \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) < 0 \ Leftrightarrow \ cos \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) > 0 USD
USD \ Leftrightarrow { 90 ^ 0 } < \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) < { 180 ^ 0 } USD . Góc USD \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) USD tù .

Hệ quả 4: Công thức tính công A của một lực tác động $\overrightarrow F $.

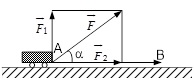
USD \ left | { \ overrightarrow F } \ right |. \ left | { \ overrightarrow { AB } } \ right |. \ cos \ varphi USD

Chứng minh

Ta có : USD \ overrightarrow F = \ overrightarrow { { F_1 } } + \ overrightarrow { { F_2 } } USD
USD A = \ overrightarrow F. \ overrightarrow { AB } = \ left ( { \ overrightarrow { { F_1 } } + \ overrightarrow { { F_2 } } } \ right ) \ overrightarrow { AB } = \ overrightarrow { { F_2 } }. \ overrightarrow { AB } USD
USD \ left | { \ overrightarrow { { F_2 } } } \ right |. \ left | { \ overrightarrow { AB } } \ right | USD
USD = \ left | { \ overrightarrow F } \ right |. \ left | { \ overrightarrow { AB } } \ right | \ cos \ varphi USD

4. Biểu thức tọa độ của tích vô hướng

Cho hai vectơ USD \ vec a ( x ; y ) ; \ vec b ( x ’ ; y ’ ) USD. Khi đó :

+ \(\vec{a}.\vec{b}=xx’+yy’\)
+ \(|\vec{a}|=\sqrt{x^2+y^2}\)
+ $cos(\vec a;\vec b) = \frac{{xx’ + yy’}}{{\sqrt {{x^2} + {y^2}} .\sqrt {{{x’}^2} + {{y’}^2}} }},(\vec a \ne \vec 0;\vec b \ne \vec 0)$
+ \(\vec{a}\perp \vec{b}\Leftrightarrow xx’+yy’=0\)

Hệ quả

Hệ quả 1. Độ dài của vectơ

Cho     $\vec{a}$ = (a1,
a2)

            $\left| {\vec{a}} \right|=\sqrt{a_{1}^{2}+a_{2}^{2}}$

Ví dụ : USD \ overrightarrow { AB } = \ left ( { – 1 ; – 2 } \ right ), \ ; \ overrightarrow { AC } = \ left ( { 4 ; – 2 } \ right ) USD. Tính USD \ left | { \ overrightarrow { AB } } \ right | USD ; USD \ left | { \ overrightarrow { AC } } \ right | USD
Giải
USD AB = \ left | { \ overrightarrow { AB } } \ right | = \ sqrt { { { \ left ( { – 1 } \ right ) } ^ 2 } + { { \ left ( { – 2 } \ right ) } ^ 2 } } = \ sqrt 5 USD
USD AC = \ left | { \ overrightarrow { AC } } \ right | = \ sqrt { { 4 ^ 2 } + { { \ left ( { – 2 } \ right ) } ^ 2 } } = 2 \ sqrt 5 USD

Hệ quả 2. Xác định Góc giữa hai vectơ khi biết tọa độ của hai véc tơ

Cho $\vec{a}$ = (a1, a2), $\vec{b}$ = (b1, b2) ($\vec{a},\vec{b}\ne \vec{0}$)

USD \ cos \ left ( { \ vec a, \ vec b } \ right ) = \ frac { { \ vec a. \ vec b } } { { \ left | { \ vec a } \ right |. \ left | { \ vec b } \ right | } } = \ frac { { { a_1 } { b_1 } + { a_2 } { b_2 } } } { { \ sqrt { a_1 ^ 2 + a_2 ^ 2 }. \ sqrt { b_1 ^ 2 + b_2 ^ 2 } } } USD
Ví dụ : Cho USD \ overrightarrow { OM } USD = ( – 2 ; – 1 ), USD \ overrightarrow { ON } USD = ( 3 ; – 1 ). Tính USD \ widehat { MON } USD ?
Giải
Ta có : USD \ cos \ left ( { \ vec a, \ vec b } \ right ) = \ frac { { \ vec a. \ vec b } } { { \ left | { \ vec a } \ right |. \ left | { \ vec b } \ right | } } USD
cos USD \ widehat { MON } USD = cos USD \ left ( \ overrightarrow { OM }, \ overrightarrow { ON } \ right ) USD
= USD \ frac { \ overrightarrow { OM }. \ overrightarrow { ON } } { \ left | \ overrightarrow { OM } \ right |. \ left | \ overrightarrow { ON } \ right | } USD
= USD \ frac { – 6 + 1 } { \ sqrt { 5 }. \ sqrt { 10 } } USD
USD = – \ frac { \ sqrt { 2 } } { 2 } USD Þ USD \ widehat { MON } USD = 1350

Hệ quả 3. Khoảng cách giữa hai điểm

Cho A ( xA ; yA ), B ( xB ; yB )
AB = USD \ sqrt { { { ( { { x } _ { B } } – { { x } _ { A } } ) } ^ { 2 } } + { { ( { { y } _ { B } } – { { y } _ { A } } ) } ^ { 2 } } } USD

Ví dụ: Cho M(–2; 2), N(1; 1). Tính MN ?

Giải : USD \ overrightarrow { AB } USD = ( xB – xA ; yB – yA )
MN = USD \ sqrt { { { ( 1 + 2 ) } ^ { 2 } } + { { ( 1-2 ) } ^ { 2 } } } USD USD = \ sqrt { 10 } USD

5. Bài tập minh họa

Bài 1:  Tính tích vô hướng của \(\vec{a}(2;3)\) và \(\vec{b}(1;1)\) biết chúng tạo với nhau một góc \(30^o\).

Giải:

Áp dụng công thức tính tích vô hướng của hai vectơ, ta có :
\ ( \ vec { a }. \ vec { b } = | \ vec { a } |. | \ vec { b } |. cos30 ^ 0 \ )
\ ( = \ sqrt { 2 ^ 2 + 3 ^ 2 }. \ sqrt { 1 ^ 2 + 1 ^ 2 }. \ frac { \ sqrt { 3 } } { 2 } = \ frac { \ sqrt { 78 } } { 2 } \ )

Bài 2: Cho hình vuông ABCD cạnh a đường chéo BD. Tính các tích vô hướng sau: \(\vec{AD}.\vec{AB}\), \(\vec{AD}.\vec{BD}\) và \(\vec{AB}.\vec{CD}\) .

Vì \ ( AD \ perp AB \ ) nên \ ( \ vec { AD }. \ vec { AB } = 0 \ )
\ ( \ vec { AD }. \ vec { BD } = | \ vec { AD } |. | \ vec { BD } | cosADB = a. a \ sqrt { 2 }. cos45 = a ^ 2 \ )
\ ( \ vec { AB }. \ vec { CD } = | \ vec { AB } |. | \ vec { CD } |. cos0 ^ o = a ^ 2 \ )

Bài 3. Cho tam giác ABC đều cạnh a, đường cao AH. Tính:

a ) USD \ overrightarrow { AB }. \ overrightarrow { AC } USD
b ) USD \ overrightarrow { AB }. \ overrightarrow { BC } USD
c ) USD \ overrightarrow { AH }. \ overrightarrow { BC } USD

Giải

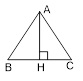
a ) USD \ overrightarrow { AB }. \ overrightarrow { AC } USD = a. a. cos600 = USD \ frac { { { a } ^ { 2 } } } { 2 } USD
b ) USD \ overrightarrow { AB }. \ overrightarrow { BC } USD = a. a. cos1200 = – USD \ frac { { { a } ^ { 2 } } } { 2 } USD
c ) USD \ overrightarrow { AH }. \ overrightarrow { BC } USD = 0

Bài 4. Cho tam giác ABC vuông tại A, AB = c, AC = b. Tính:

a ) USD \ overrightarrow { BA }. \ overrightarrow { BC } USD
b ) USD \ overrightarrow { CA }. \ overrightarrow { CB } USD

Giải

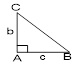
a ) cos ( USD \ overrightarrow { BA }, \ overrightarrow { BC } USD ) = USD \ frac { c } { \ sqrt { { { b } ^ { 2 } } + { { c } ^ { 2 } } } } USD
=> USD \ overrightarrow { BA }. \ overrightarrow { BC } USD = c2

b)
$\begin{array}{l}
\cos \left( {\overrightarrow {CA} ,\overrightarrow {CB} } \right) = \frac{b}{{\sqrt {{b^2} + {c^2}} }}\\
\Rightarrow \overrightarrow {CA} .\overrightarrow {CB} = b.\sqrt {{b^2} + {c^2}} .\frac{b}{{\sqrt {{b^2} + {c^2}} }} = {b^2}
\end{array}$

Bài 5. Cho tam giác ABC đều cạnh a. Tính:

USD \ overrightarrow { AB }. \ overrightarrow { BC } + \ overrightarrow { BC }. \ overrightarrow { CA } + \ overrightarrow { CA }. \ overrightarrow { AB } USD

Đáp số: $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} = – \frac{{3{a^2}}}{2}$

6. Bài tập vân dụng

Cho A ( 1 ; 1 ), B ( 2 ; 3 ), C ( – 1 ; – 2 ) .
a ) Xác định điểm D sao cho ABCD là hình bình hành .
b ) Tính chu vi hbh ABCD .
c ) Tính góc A .

Hướng dẫn

ABCD là hình bình hành khi và chi khi:
$\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}
{x_D} = – 2\\
{y_D} = – 4
\end{array} \right.$

b ) AB = USD \ sqrt { { { 1 } ^ { 2 } } + { { 2 } ^ { 2 } } } = \ sqrt { 5 } USD
AD = USD \ sqrt { { { 3 } ^ { 2 } } + { { 5 } ^ { 2 } } } = \ sqrt { 34 } USD

cosA = cos$\left( \overrightarrow{AB},\overrightarrow{AD} \right)$
= $\frac{\overrightarrow{AB}.\overrightarrow{AD}}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{AD} \right|}$
= $\frac{-3-10}{\sqrt{5}.\sqrt{34}}=-\frac{13}{\sqrt{170}}$

Củng cố kim chỉ nan qua sơ đồ tư duy

Trắc nghiệm

Câu 1: Cho vectơ \(\vec{a}(4;3)\) và vectơ \(\vec{b}(-3;4)\). Góc hợp bởi 2 vectơ trên là \(90^o\). Tích vô hướng của hai vectơ là:

A. 0
B. \(\frac{25}{2}\)
C. \(\frac{25\sqrt{3}}{2}\)
D. \(5\sqrt{2}\)

Câu 2: Cho $\vec a(1;3)$ và $\vec b( – 2;4)$. Góc tạo bởi hai vectơ trên là:

A. \(30^o\)
B. \(45^o\)
C. \(60^o\)
D. \(75^o\)

Câu 3: Chu vi của tam giác ABC có tọa độ ba điểm lần lượt là (A(1;1);B(2;6);C(-2;4)) bằng?

A. \(\approx 10,219\)
B. \(\approx 13,813\)
C. \(\approx 14,767\)
D. \(\approx 17,532\)

Câu 3: Cho hai vectơ $\vec a = 2\vec i + \vec j$ và $\vec b = k\vec i – \vec j$. Giá trị của k để $\vec a \bot \vec b$ là:

A. \(k=\frac{1}{3}\)
B. \(k=\frac{-1}{3}\)
C. \(k=\frac{1}{2}\)
D. \(k=\frac{-1}{2}\)

Câu 4. Cho hình bình hành ABCD có độ dài các đường chéo AC= 6, BD= 8. Giá trị của tích vô hướng của vecto AB nhân vecto AD là:

A. 5 B. – 7 C. 7 D. 25

Bài tập tự luận

Bài 1. Cho tam giác ABC không cân. Đường tròn tâm I nội tiếp tam giác, tiếp xúc với các cạnh BC, CA, AB lần lượt tại A’, B’, C’. Đường thằng B’C’ cắt BC tại D. Chứng minh ID vuông góc với AA’

Bài 2. Cho hình chữ nhật ABCD. Gọi E là hình chiếu cuarB trên AC, F và G là trung điểm của AE và CD. Chứng minh BF vuông góc với FG

— — — — — —

Download tài liệu: PDF-tại đây Word: tại đây.

Xem thêm:

— — — — — — — –

Source: http://wp.ftn61.com
Category: Thủ Thuật