Cách tìm tiệm cận đứng tiệm cận ngang của hàm số nhanh nhất!

Tiệm cận là một chủ đề quan trọng trong các bài toán hàm số THPT. Vậy khái niệm tiệm cận là gì? Cách tìm tiệm cận đứng tiệm cận ngang tiệm cận xiên? Cách tìm tiệm cận hàm số chứa căn? Cách bấm máy tìm tiệm cận?… Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề  trên, cùng tìm hiểu nhé!. 

Định nghĩa tiệm cận là gì?

Tiệm cận ngang là gì?

Đường thẳng \ ( y = y_0 \ ) được gọi là tiệm cận ngang của hàm số \ ( y = f ( x ) \ ) nếu :

\(\lim_{x\rightarrow +\infty}y=y_0\) hoặc \(\lim_{x\rightarrow -\infty}y=y_0\)

Tiệm cận đứng là gì? 

Đường thẳng \ ( x = x_0 \ ) được gọi là tiệm cận đứng của hàm số \ ( y = f ( x ) \ ) nếu tối thiểu một trong những điều kiện kèm theo sau thỏa mãn nhu cầu :
\ ( \ left [ \ begin { array } { l } \ lim_ { x \ rightarrow x_0 ^ { – } } y = + \ infty \ \ \ lim_ { x \ rightarrow x_0 ^ { + } } y = + \ infty \ \ \ lim_ { x \ rightarrow x_0 ^ { – } } y = – \ infty \ \ \ lim_ { x \ rightarrow x_0 ^ { + } } y = – \ infty \ end { array } \ right. \ )

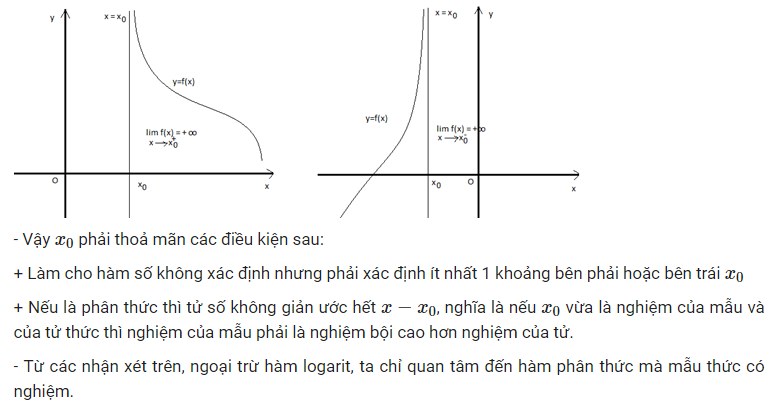
Tiệm cận xiên là gì?

Đường thẳng \ ( y = ax_b \ ) được gọi là tiệm cận xiên của hàm số \ ( y = f ( x ) \ ) nếu :
\ ( \ lim_ { x \ rightarrow + \ infty } | f ( x ) – ( ax + b ) | = 0 \ ) hoặc \ ( \ lim_ { x \ rightarrow – \ infty } | f ( x ) – ( ax + b ) | = 0 \ )

Xem chi tiết >>> Lý thuyết đường tiệm cận là gì? 

Dấu hiệu nhận biết tiệm cận đứng tiệm cận ngang 

• Hàm phân thức khi nghiệm của mẫu không là nghiệm của tử có tiệm cận đứng .
• Hàm phân thức khi bậc tử bé hơn hoặc bằng bậc của mẫu có tiệm cận ngang .
• Hàm căn thức có dạng như sau thì có tiệm cận ngang ( Dạng này dùng phối hợp để giải ) .

Cách tìm tiệm cận của hàm số

Cách tìm tiệm cận ngang

Để tìm tiệm cận ngang của hàm số \ ( y = f ( x ) \ ) thì ta tính \ ( \ lim_ { x \ rightarrow + \ infty } y \ ) và \ ( \ lim_ { x \ rightarrow – \ infty } y \ ). Nếu số lượng giới hạn là 1 số ít thực \ ( a \ ) thì đường thẳng \ ( y = a \ ) là tiệm cận ngang của hàm số

Ví dụ 1:

Tìm tiệm cận ngang của hàm số \ ( y = \ frac { x-2 } { 2 x – 1 } \ )

Cách giải:

TXĐ : \ ( x \ in \ mathbb { R } \ setminus \ begin { Bmatrix } \ frac { 1 } { 2 } \ end { Bmatrix } \ )
Ta có :
\ ( \ lim_ { x \ rightarrow + \ infty } \ frac { x-2 } { 2 x – 1 } = \ lim_ { x \ rightarrow + \ infty } \ frac { 1 – \ frac { 2 } { x } } { 2 – \ frac { 1 } { x } } = \ frac { 1 } { 2 } \ )
\ ( \ lim_ { x \ rightarrow – \ infty } \ frac { x-2 } { 2 x – 1 } = \ lim_ { x \ rightarrow – \ infty } \ frac { 1 – \ frac { 2 } { x } } { 2 – \ frac { 1 } { x } } = \ frac { 1 } { 2 } \ )
Vậy hàm số có một tiệm cận ngang \ ( y = \ frac { 1 } { 2 } \ )

Ví dụ 2:

Ví dụ 3 :

Cách tìm tiệm cận ngang bằng máy tính

Để tìm tiệm cận ngang bằng máy tính, tất cả chúng ta sẽ tính gần đúng giá trị của \ ( \ lim_ { x \ rightarrow + \ infty } y \ ) và \ ( \ lim_ { x \ rightarrow – \ infty } y \ ) .
Để tính \ ( \ lim_ { x \ rightarrow + \ infty } y \ ) thì tất cả chúng ta tính giá trị của hàm số tại một giá trị \ ( x \ ) rất lớn. Ta thường lấy \ ( x = 10 ^ 9 \ ). Kết quả là giá trị gần đúng của \ ( \ lim_ { x \ rightarrow + \ infty } y \ )
Tương tự, để tính \ ( \ lim_ { x \ rightarrow – \ infty } y \ ) thì tất cả chúng ta tính giá trị của hàm số tại một giá trị \ ( x \ ) rất nhỏ. Ta thường lấy \ ( x = – 10 ^ 9 \ ). Kết quả là giá trị gần đúng của \ ( \ lim_ { x \ rightarrow – \ infty } y \ )
Để tính giá trị hàm số tại một giá trị của \ ( x \ ), ta dung tính năng CALC trên máy tính .

Ví dụ:

Tìm tiệm cận ngang của hàm số \ ( y = \ frac { 3 – x } { 3 x + 1 } \ )

Cách giải:

TXĐ : \ ( x \ in \ mathbb { R } \ setminus \ begin { Bmatrix } \ frac { – 1 } { 3 } \ end { Bmatrix } \ )
Ta nhập hàm số vào máy tính Casio :

Tiếp theo, ta bấm CALC rồi nhập giá trị \ ( 10 ^ 9 \ ) rồi bấm dấu “ = ”. Ta được tác dụng :

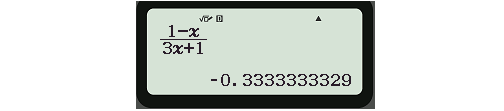
Kết quả này giao động bằng \ ( – \ frac { 1 } { 3 } \ ). Vậy ta có \ ( \ lim_ { x \ rightarrow + \ infty } \ frac { 3 – x } { 3 x + 1 } = – \ frac { 1 } { 3 } \ )
Tương tự ta cũng có \ ( \ lim_ { x \ rightarrow – \ infty } \ frac { 3 – x } { 3 x + 1 } = – \ frac { 1 } { 3 } \ )
Vậy hàm số có một tiệm cận ngang là đường thẳng \ ( y = – \ frac { 1 } { 3 } \ )

Cách tìm tiệm cận đứng

Để tìm tiệm cận đứng của hàm số dạng \ ( \ frac { f ( x ) } { g ( x ) } \ ) thì ta làm những bước như sau :

• Bước 1:Tìm nghiệm của phương trình \ ( g ( x ) = 0 \ )
• Bước 2:Trong số những nghiệm tìm được ở bước trên, loại những giá trị là nghiệm của hàm số \ ( f ( x ) \ )
• Bước 3:Những nghiệm \ ( x_0 \ ) còn lại thì ta được đường thẳng \ ( x = x_0 \ ) là tiệm cận đứng của hàm số

Ví dụ:

Tìm tiệm cận đứng của hàm số \ ( y = \ frac { x ^ 2-1 } { x ^ 2-3 x + 2 } \ )

Cách giải:

Xét phương trình : \ ( x ^ 2-3 x + 2 = 0 \ )
\ ( \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ x = 2 \ end { array } \ right. \ )
Nhận thấy \ ( x = 1 \ ) cũng là nghiệm của phương trình \ ( x ^ 2-1 = 0 \ )
\ ( x = 2 \ ) không là nghiệm của phương trình \ ( x ^ 2-1 = 0 \ )
Vậy ta được hàm số đã cho có một tiệm cận đứng là đường thẳng \ ( x = 2 \ )

Ví dụ 1: Cách tìm tiệm cận

Ví dụ 2 :

Cách tìm tiệm cận đứng bằng máy tính

Để tìm tiệm cận đứng của hàm số dạng \ ( \ frac { f ( x ) } { g ( x ) } \ ) bằng máy tính thì tiên phong ta cũng tìm nghiệm của hàm số \ ( g ( x ) \ ) rồi sau đó loại những giá trị cũng là nghiệm của hàm số \ ( f ( x ) \ )

• Bước 1:Sử dụng tính năng SOLVE để giải nghiệm. Nếu mẫu số là hàm bậc \ ( 2 \ ) hoặc bậc \ ( 3 \ ) thì ta hoàn toàn có thể dùng tính năng Equation ( EQN ) để tìm nghiệm
• Bước 2: Dùng tính năng CALC để thử những nghiệm tìm được có là nghiệm của tử số hay không .
• Bước 3:Những giá trị \ ( x_0 \ ) là nghiệm của mẫu số nhưng không là nghiệm của tử số thì đường thẳng \ ( x = x_0 \ ) là tiệm cận đứng của hàm số .

Ví dụ:

Tìm tiệm cận đứng của hàm số : \ ( y = \ frac { 2 x – 1 – \ sqrt { x ^ 2 + x + 3 } } { x ^ 2-5 x + 6 } \ )

Cách giải:

Tìm nghiệm phương trình \ ( x ^ 2-5 x + 6 = 0 \ )
Trên máy tính Casio Fx 570ES, bấm \ ( Mode \ rightarrow 5 \ rightarrow 3 \ ) để vào chính sách giải phương trình bậc \ ( 2 \ )
Lần lượt bấm để nhập những giá trị \ ( 1 \ rightarrow = \ rightarrow – 5 \ rightarrow = \ rightarrow 6 \ rightarrow = \ rightarrow = \ )

Kết quả ta được hai nghiệm \ ( x = 2 \ ) và \ ( x = 3 \ )
Sau đó, ta nhập tử số vào máy tính :

Bấm CALC rồi thay từng giá trị \ ( x = 2 \ ) và \ ( x = 3 \ )
Ta thấy với \ ( x = 2 \ ) thì tử số bằng \ ( 0 \ ) và với \ ( x = 3 \ ) thì tử số khác \ ( 0 \ )
Vậy Tóm lại \ ( x = 3 \ ) là tiệm cận đứng của hàm số .

Cách tìm tiệm cận xiên

Hàm số \ ( y = \ frac { f ( x ) } { g ( x ) } \ ) có tiệm cận xiên nếu bậc của \ ( f ( x ) \ ) lớn hơn bậc của \ ( g ( x ) \ ) một bậc và \ ( f ( x ) \ ) không chia hết cho \ ( g ( x ) \ )
Nếu hàm số không phải hàm phân thức thì ta coi như là hàm phân thức với bậc của mẫu số bằng \ ( 0 \ )
Sau khi xác lập hàm số có tiệm cận xiên, ta triển khai tìm tiệm cận xiên như sau :

• Bước 1:Rút gọn hàm số về dạng tối giản
• Bước 2:Tính số lượng giới hạn \ ( \ lim_ { x \ rightarrow + \ infty } \ frac { y } { x } = a \ neq 0 \ ) hoặc \ ( \ lim_ { x \ rightarrow + \ infty } \ frac { y } { x } = a \ neq 0 \ )
• Bước 3:Tính số lượng giới hạn \ ( \ lim_ { x \ rightarrow + \ infty } ( y-ax ) = b \ ) hoặc \ ( \ lim_ { x \ rightarrow – \ infty } ( y-ax ) = b \ )
• Bước 4:Kết luận đường thẳng \ ( y = ax + b \ ) là tiệm cận xiên của hàm số .

Ví dụ:

Tìm tiệm cận xiên của hàm số \ ( y = \ frac { x ^ 3-4 x ^ 2 + 2 x + 1 } { x ^ 2 – x-2 } \ )

Cách giải:

Ta có :
\ ( y = \ frac { x ^ 3-4 x ^ 2 + 2 x + 1 } { x ^ 2 + x-2 } = \ frac { ( x ^ 2-3 x – 1 ) ( x-1 ) } { ( x-1 ) ( x + 2 ) } = \ frac { x ^ 2-3 x – 1 } { x + 2 } \ )
Nhận thấy bậc của tử số lớn hơn một bậc so với bậc của mẫu số. Vậy hàm số có tiệm cận xiên .
\ ( \ lim_ { x \ rightarrow + \ infty } \ frac { x ^ 2-3 x – 1 } { x ( x + 2 ) } = \ lim_ { x \ rightarrow – \ infty } \ frac { x ^ 2-3 x – 1 } { x ( x + 2 ) } = 1 \ )

\(\lim_{x\rightarrow \infty}[\frac{x^2-3x-1}{(x+2)}-x]=\lim_{x\rightarrow \infty}\frac{-3x-1}{x+2}=-3\)

Vậy đường thẳng \ ( y = x-3 \ ) là tiệm cận xiên của hàm số .

Cách tìm tiệm cận xiên bằng máy tính

Chúng ta cũng làm theo những bước như trên nhưng thay vì tính \ ( \ lim_ { x \ rightarrow \ infty } \ frac { y } { x } \ ) và \ ( \ lim_ { x \ rightarrow \ infty } ( y-ax ) \ ) thì ta sử dụng tính năng CALC để tính giá trị gần đúng .

Ví dụ:

Tìm tiệm cận xiên của hàm số \ ( y = \ frac { 1 – x ^ 2 } { x + 2 } \ )

Cách giải:

Tìm \ ( \ lim_ { x \ rightarrow \ infty } \ frac { 1 – x ^ 2 } { ( x + 2 ) } \ ) bằng cách tính giá trị gần đúng của tại giá trị \ ( 10 ^ 9 \ )
Nhập hàm số vào máy tính, bấm CALC \ ( 10 ^ 9 \ ) ta được :

Giá trị này giao động \ ( – 1 \ ). Vậy \ ( \ lim_ { x \ rightarrow \ infty } \ frac { 1 – x ^ 2 } { ( x + 2 ) } = – 1 \ )
Tương tự, ta dùng tính năng CALC để tính \ ( \ lim_ { x \ rightarrow \ infty } ( \ frac { 1 – x ^ 2 } { x + 2 } + x ) = 2 \ )
Vậy đường thẳng \ ( y = – x + 2 \ ) là tiệm cận xiên của hàm số .

Cách tìm tiệm cận nhanh

Cách bấm máy tìm tiệm cận

Như phần trên đã hướng dẫn, cách tìm tiệm cận bằng máy tính là cách thường được sử dụng để xử lý nhanh những bài toán trắc nghiệm nhu yếu vận tốc cao. Đó cũng chính là cách bấm máy tìm tiệm cận nhanh dành cho bạn .

Cách xác định tiệm cận qua bảng biến thiên

Một số bài toán cho bảng biến thiên nhu yếu tất cả chúng ta xác lập tiệm cận. Ở những bài toán này thì tất cả chúng ta chỉ xác lập được tiệm cận đứng, tiệm cận ngang chứ không xác lập được tiệm cận xiên ( nếu có ) .
Để xác lập được tiệm cận dựa vào bảng biến thiên thì tất cả chúng ta cần nắm chắc định nghĩa tiệm cận đứng, tiệm cận ngang để nghiên cứu và phân tích dựa trên 1 số ít đặc thù sau đây :

• Tiệm cận đứng ( nếu có ) là những điểm mà hàm số không xác lập .
• Tiệm cận ngang ( nếu có là giá trị của hàm số khi \ ( x \ rightarrow \ infty \ )

Ví dụ:

Cho hàm số \ ( f ( x ) \ ) có bảng biến thiên như hình vẽ. Hãy xác lập những đường tiệm cận của hàm số .

Cách giải:

• Tiệm cận ngang:

Ta thấy khi \ ( x \ rightarrow + \ infty \ ) thì \ ( y \ rightarrow 0 \ ). Vậy \ ( y = 0 \ ) là tiệm cận ngang của hàm số
Hàm số không xác lập tại \ ( – \ infty \ )
Vậy hàm số chỉ có một tiệm cận ngang là \ ( y = 0 \ )

• Tiệm cận đứng:

Ta xét những giá trị của \ ( x \ ) mà tại đó \ ( y \ ) đạt giá trị \ ( \ infty \ )
Dễ thấy có hai giá trị của \ ( x \ ) đó là \ ( x = – 2 \ ) và \ ( x = 0 \ )
Vậy hàm số có hai tiệm cận đứng là \ ( x = – 2 \ ) và \ ( x = 0 \ )

Cách tìm số tiệm cận nhanh nhất

Để xác lập số đường tiệm cận của hàm số, ta chú ý quan tâm đặc thù sau đây :
Cho hàm số dạng \ ( y = \ frac { P. ( x ) } { Q. ( x ) } \ )

• Nếu \ ( \ left \ { \ begin { matrix } P. ( x_0 ) \ neq 0 \ \ Q. ( x_0 ) = 0 \ end { matrix } \ right. \ ) thì \ ( x = x_0 \ ) là tiệm cận đứng của hàm số
• Nếu bậc của \ ( P. ( x ) \ ) nhỏ hơn bậc của \ ( Q. ( x ) \ ) thì hàm số có tiệm cận ngang là đường thẳng \ ( y = 0 \ )
• Nếu bậc của \ ( P. ( x ) \ ) bằng bậc của \ ( Q. ( x ) \ ) thì hàm số có tiệm cận ngang là đường thẳng \ ( y = \ frac { a } { b } \ ) với \ ( a ; b \ ) lần lượt là thông số của số hạng có số mũ lớn nhất của \ ( P. ( x ) ; Q. ( x ) \ )
• Nếu bậc của \ ( P. ( x ) \ ) lớn hơn bậc của \ ( Q. ( x ) \ ) một bậc và \ ( P. ( x ) \ ) không chia hết cho \ ( Q. ( x ) \ ) thì hàm số có tiệm cận xiên là đường thẳng \ ( y = ax + b \ ) với :
  • \ ( a = \ lim_ { x \ rightarrow \ infty } \ frac { P. ( x ) } { xQ ( x ) } \ )
  • \ ( b = \ lim_ { x \ rightarrow \ infty } ( P. ( x ) – ax ) \ )
• Nếu bậc của \ ( P. ( x ) \ ) lớn hơn bậc của \ ( Q. ( x ) \ ) từ hai bậc trở lên thì hàm số không có tiệm cận ngang cũng như tiệm cận xiên .

Dựa vào những đặc thù trên, ta hoàn toàn có thể giám sát hoặc sử dụng cách tìm số đường tiệm cận bằng máy tính như đã nói ở trên để giám sát tìm ra số đường tiệm cận của hàm số .

Ví dụ:

Tìm số đường tiệm cận của hàm số \ ( y = \ frac { 2 x + 1 – \ sqrt { 3 x + 1 } } { x ^ 2 – x } \ )

Cách giải:

Ta có :
Mẫu số \ ( x ^ 2 – x \ ) có hai nghiệm là \ ( x = 0 \ ) và \ ( x = 1 \ )
Thay vào tử số, ta thấy \ ( x = 0 \ ) là nghiệm của tử số còn \ ( x = 1 \ ) không là nghiệm
Vậy hàm số có một tiệm cận đứng là \ ( x = 1 \ )
Dễ thấy bậc của tử số là \ ( 1 \ ) còn bậc của mẫu số là \ ( 2 \ ). Dựa vào đặc thù nêu trên ta có : Hàm số có một tiệm cận ngang là \ ( y = 0 \ )
Vậy hàm số đã cho có tổng thể \ ( 2 \ ) đường tiệm cận .

Tìm hiểu cách tìm tiệm cận của hàm số chứa căn

Một số bài toán nhu yếu tìm tiệm cận của hàm số đặc biệt quan trọng như tìm tiệm cận của hàm số toán hạng sang, tìm tiệm cận của hàm số chứa căn. Tùy thuộc vào mỗi bài toán sẽ có những giải pháp riêng nhưng đa phần tất cả chúng ta vẫn dựa trên những bước đã nêu ở trên .

Cách tìm tiệm cận hàm số căn thức

Với những hàm số dạng \ ( y = \ sqrt { ax ^ 2 + bx + c } \ ) với \ ( a > 0 \ ), ta xét số lượng giới hạn
\ ( \ lim_ { x \ rightarrow \ infty } ( \ sqrt { ax ^ 2 + bx + c } – \ sqrt { a } | x + \ frac { b } { 2 a } | ) = 0 \ )
Từ đó suy ra đường thẳng \ ( y = \ sqrt { a } ( x + \ frac { b } { 2 a } ) \ ) là tiệm cận xiên của hàm số \ ( y = \ sqrt { ax ^ 2 + bx + c } \ ) với \ ( a > 0 \ )

Ví dụ:

Tìm tiệm cận xiên của hàm số \ ( y = x + 1 + \ sqrt { x ^ 2 + 2 } \ )

Cách giải:

Từ công thức trên, ta có :
\ ( \ lim_ { x \ rightarrow \ infty } ( \ sqrt { x ^ 2 + 2 } – x ) = 0 \ )
\ ( \ Rightarrow \ lim_ { x \ rightarrow \ infty } ( y-2x-1 ) = 0 \ )
Vậy hàm số đã cho có tiệm cận xiên là đường thẳng \ ( y = 2 x + 1 \ )

Cách tìm tiệm cận hàm số phân thức chứa căn

Với những hàm số này, tất cả chúng ta vẫn làm theo những bước như hàm số phân thức thông thường nhưng cần quan tâm rằng : Bậc của \ ( \ sqrt [ n ] { f ( x ) } \ ) bằng \ ( \ frac { 1 } { n } \ ) bậc của \ ( f ( x ) \ )

Ví dụ:

Tìm tiệm cận của hàm số \ ( y = \ frac { x \ sqrt { 2 x + 5 } \ sqrt { 2 } x } { \ sqrt { x + 2 } – 1 } \ )

Cách giải:

TXĐ : TXĐ : \ ( x \ in \ mathbb { R } \ setminus \ begin { Bmatrix } ( – \ infty ; – 2 ) \ end { Bmatrix } \ )
Ta có :
Dễ thấy \ ( x = – 1 \ ) không là nghiệm của tử số. Vậy hàm số có tiệm cận đứng \ ( x = – 1 \ )
Nhận thấy bậc của tử số là \ ( \ frac { 3 } { 2 } \ ), bậc của mẫu số là \ ( \ frac { 1 } { 2 } \ ). Như vậy bậc của tử số lớn hơn bậc của mẫu số nên hàm số không có tiệm cận ngang .
\ ( \ lim_ { x \ rightarrow \ infty } \ frac { x \ sqrt { 2 x + 5 } } { x ( \ sqrt { x + 2 } – 1 ) } = \ sqrt { 2 } \ )
\ ( \ lim_ { x \ rightarrow \ infty } ( \ frac { x \ sqrt { 2 x + 5 } – \ sqrt { 2 } x } { \ sqrt { x + 2 } – 1 } – \ sqrt { 2 } x ) = \ lim_ { x \ rightarrow \ infty } \ frac { x } { ( \ sqrt { 2 x + 5 } + \ sqrt { 2 x + 4 } ) ( \ sqrt { x + 2 } – 1 ) } = \ frac { 1 } { 2 \ sqrt { 2 } } \ )
Vậy hàm số có tiệm cận xiên là đường thẳng \ ( y = \ sqrt { 2 } x + \ frac { 1 } { 2 \ sqrt { 2 } } \ )

Bài tập cách tìm tiệm cận đứng tiệm cận ngang

Dạng 1: Bài toán không chứa tham số

Dạng 2: Bài toán có chứa tham số

Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp lý thuyết và các phương pháp giải bài tập tiệm cận. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chủ đề cách tìm tiệm cận đứng tiệm cận ngang. Chúc bạn luôn học tốt!

Xem chi tiết cụ thể qua bài giảng dưới đây :

(Nguồn: www.youtube.com)

Xem thêm :

3
/
5
(
2
bầu chọn

)

Please follow and like us :

Source: http://wp.ftn61.com
Category: Hỏi Đáp