Tóm tắt nội dung bài viết
Định lý Vi-et trong phương trình bậc 2, bậc 3, bậc 4 Toán Lớp 9
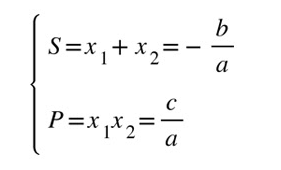
Định lý Vi-et là định lý quan trọng với nội dung Toán mà tất cả chúng ta tiếp đón. Nhờ định lý Viet bạn hoàn toàn có thể giải được nhiều bài toán với những cách hay và nhanh gọn
Hãy theo dõi bài viết dưới đây của chúng tôi để hoàn toàn có thể hiểu hơn về chủ đề này nhé !
Định lý Vi-et là gì ?
– Định lý Viet là công thức bộc lộ mối quan hệ giữa những nghiệm của phương trình đa thức trong trường số phức và những thông số do nhà toán học Pháp François Viète tìm ra. Viète được phiên âm theo tiếng Việt là Vi-ét
1. Định lý Vi-et thuận
– Cho phương trình bậc 2 một ẩn : ax ^ 2 + bx + c = 0 ( a ≠ 0 ) ( * ) có 2 nghiệm x1 và x2. Khi đó 2 nghiệm tìm được thỏa mãn nhu cầu hệ thức sau :
– Hệ quả: Dựa vào định lý Viét khi phương trình bậc 2 một ẩn có nghiệm, ta có thể nhẩm nghiệm trực tiếp của phương trình trong một số trường hợp đặc biệt:
Nếu a + b + c = 0 thì (*) có 1 nghiệm x1 = 1 và x2 = a/c
Nếu a – b + c = 0 thì ( * ) có nghiệm x1 = – 1 và x2 = – c / a
2. Định lý Vi-et đảo
Giả sử hai số thực x1 và x2 thỏa mãn nhu cầu hệ thức :
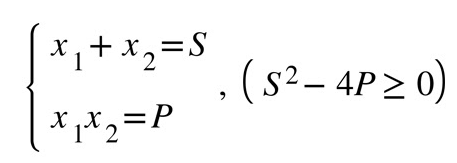
==> Thì x1 và x2 là 2 nghiệm của phương trình bậc 2: x^2 – Sx + P=0 (1).
Chú ý: điều kiện S^2 – 4P ≥ 0 là bắt buộc. Đây là điều kiện để ∆(1) ≥ 0 hay đây là điều kiện để phương trình bậc 2 tồn tại nghiệm.
Định lý Vi- et bậc 3
Định lý Vi- et bậc 4
– Nếu phương trình bậc 4: ax^4 + bx^3 + cx^2 + dx + e = 0 ( với a ≠ 0 ) có 4 nghiệm X1, X2, X3 thì:
– Định lý Vi-et được vận dụng trong rất nhiều nghành như vật lý – dùng để giải những bài toán hiệu suất mạch xoay chiều – hay hoá học, địa chất …. Vì thế Định lý Vi-et được dùng cho cả Toán – Lý – Hóa
Với nội dung bài viết này, chúng tôi kỳ vọng bạn sẽ hiểu hơn về định lý Viet cũng như giải quyết và xử lý được những bài toán, những yếu tố nan giải của mình nhé !
Source: http://wp.ftn61.com
Category: Hỏi Đáp

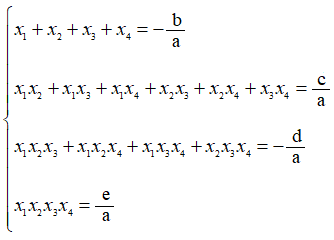



Để lại một bình luận