Cách Viết Phương Trình Tiếp Tuyến Song Song Với Đường Thẳng, Viết Phương Trình Tiếp Tuyến Của Đồ Thị Hàm Số

Trong chương trình toán học THPT, cách viết phương trình tiếp tuyến là chủ đề quan trọng đối với các bạn học sinh. Vậy viết phương trình tiếp tuyến tại 1 điểm như nào? Kiến thức viết phương trình tiếp tuyến của hàm số?… Trong nội dung bài viết dưới đây, hãy cùng lingocard.vn tìm hiểu chi tiết và cụ thể về chủ đề trên nhé!. 

Các dạng bài tập về cách viết phương trình tiếp tuyến

Viết phương trình tiếp tuyến tại tiếp điểm M.Viết phương trình tiếp tuyến đi qua điểm A cho trước. Viết phương trình tiếp tuyến biết thông số góc k .

Đang xem: Viết phương trình tiếp tuyến song song với đường thẳng

Phương trình tiếp tuyến tại tiếp điểm ( M ( x_ { 0 }, y_ { 0 } ) ) có dạng :
( y = f ^ { ‘ } ( x_ { 0 } ) ( x-x_ { 0 } ) + y_ { 0 } ) ( 1 )

Trong đó ( f ^ { ‘ } ( x_ { 0 } ) ) là đạo hàm của hàm số tại điểm ( x_ { 0 } ) .
( x_ { 0 } ; y_ { 0 } ) là hoành độ, tung độ của tiếp điểm M .
Xem thêm : nghị luận văn học tây tiến
Như vậy với bài tập nhu yếu viết phương trình tiếp tuyến thì ta phải tìm 3 đại lượng, là : ( f ” ( x_ { 0 } ) ; x_ { 0 } và y_ { 0 } ) .
Xem thêm : Giải Vở Bài Tập Toán Lớp 2 Tập 2 Trang 97 Vở Bài Tập ( Vbt ) Toán 2 Tập 1

Cách viết phương trình tiếp tuyến tại tiếp điểm 

Để viết phương trình tiếp tuyến tại tiếp điểm cho trước ( M ( x_ { 0 }, y_ { 0 } ) )

Cách làm: Bài toán yêu cầu viết phương trình tiếp tuyến tại tiếp điểm (M(x_{0},y_{0})) thì công việc cần làm là tìm (f”(x_{0}); x_{0} và y_{0}), trong đó (x_{0}, y_{0}) chính là tọa độ của điểm M, vì vậy chỉ cần tính (f”(x_{0})), rồi thay vào phương trình (1) là xong.

Cách viết phương trình tiếp tuyến đi qua một điểm

Cho đồ thị hàm số y = f ( x ), viết phương trình tiếp tuyến ( Delta ) của đồ thị hàm số biết tiếp tuyến đi qua A ( a, b )

Phương pháp:

Gọi phương trình tiếp tuyến của (Delta) có dạng: y = f’x_{0}(x – x_{0}) + y_{0} (2)

Và có tiếp điểm ( M_ { 0 } ( x_ { 0 }, y_ { 0 } ) )
Vì A ( a, b ) thuộc tiếp tuyến nên thay tọa độ A vào phương trình ta có :
( b = f ’ _ { x_ { 0 } } ( a – x_ { 0 } ) + f_ { x_ { 0 } } ) với ( f_ { x_ { 0 } } = y_ { 0 } )
Phương trình này chỉ chứa ẩn ( x_ { 0 } ), do đó chỉ cần giải phương trình trên để tìm ( x_ { 0 } ) .
Sau đó sẽ tìm được ( f’x _ { 0 } và y_ { 0 } ) .
Tới đây phương trình tiếp tuyến của tất cả chúng ta đã tìm được .

Cách viết phương trình tiếp tuyến có hệ số góc k

Để viết phương trình tiếp tuyến ( Delta ) của đồ thị ( C ) y = f ( x ) khi thông số góc k ta làm theo những bước sau :

Bước 1: Tính đạo hàm f’(x)Bước 2: Giải phương trình f’(x) = k để tìm hoành độ (x_{0}) của tiếp điểm. Từ đây suy ra tọa độ điểm (M_{0}(x_{0}; y_{0})) với (y_{0} = f(x_{0}))Bước 3: Viết phương trình tiếp tuyến (Delta) tại tiếp điểm (M_{0}(x_{0}; y_{0})):

( y = f ” ( x_ { 0 } ) ( x – x_ { 0 } ) + y_ { 0 } )

***Chú ý: Tính chất của hệ số góc k của tiếp tuyến

Tiếp tuyến song song với đường thẳng y = ax + b thì k = aTiếp tuyến vuông góc với đường thẳng y = ax + b thì ( k = – frac { 1 } { a } )

Phương trình tiếp tuyến song song với đường thẳng

Vì tiếp tuyến song song với đường thẳng y = ax + b nên tiếp tuyến có thông số góc k = a. Phương trình tiếp tuyến của ( C ) đi qua tiếp điểm ( M ( x_ { _ { 0 } }, y_ { 0 } ) ) là ( y = a ( x-x_ { 0 } ) + y_ { 0 } )

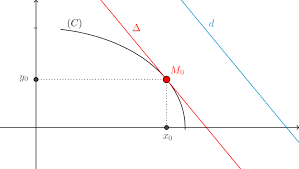
Phương trình tiếp tuyến vuông góc với đường thẳng

Vì tiếp tuyến vuông góc với đường thẳng có phương trình y = ax + b nên tiếp tuyến có thông số góc ( k = – frac { 1 } { a } )
Phương trình tiếp tuyến của ( C ) đi qua tiếp điểm ( M ( x_ { _ { 0 } }, y_ { 0 } ) ) là ( – frac { 1 } { a } ( x-x_ { 0 } ) + y_ { 0 } )

Xem thêm bài viết thuộc chuyên mục: Phương trình

Điều hướng bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp