- A\(M\left( 0;3 \right)\)
-
B
\(M\left( -1;5 \right)\)
- C \(M\left( -2;1 \right)\)
- D \(M\left( 2;-1 \right)\)
Đáp án: C
Phương pháp giải :Phương trình tiếp tuyến của hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm \ ( { { x } _ { 0 } } \ ) là \ ( y-f \ left ( { { x } _ { 0 } } \ right ) = f ‘ \ left ( x { { } _ { 0 } } \ right ) \ left ( x – { { x } _ { 0 } } \ right ). \ )
Viết phương trình tiếp tuyến sau đó tìm hoành độ giao điểm của phương trình tiếp tuyến với đồ thị hàm số để tìm giao điểm thứ \ ( 2. \ )Lời giải chi tiết cụ thể :Ta có \ ( y ‘ = 3 { { x } ^ { 2 } } – 3 \ Rightarrow y ‘ \ left ( 1 \ right ) = 0. \ ) Do đó tiếp tuyến tại \ ( N \ left ( 1 ; 1 \ right ) \ ) có dạng \ ( y-1 = y ‘ \ left ( 1 \ right ) \ left ( x-1 \ right ) \ Leftrightarrow d : y = 1. \ ) Khi đó \ ( d \ cap \ left ( C \ right ) \ ) có hoành độ giao điểm là \ ( { x ^ 3 } – 3 x + 3 = 1 \ Leftrightarrow { x ^ 3 } – 3 x + 2 = 0 \ Leftrightarrow { \ left ( { x – 1 } \ right ) ^ 2 } \ left ( { x + 2 } \ right ) = 0 \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ x = – 2. \ end { array } \ right. \ )
Giao điểm thứ \ ( 2 \ ) của \ ( d \ ) và \ ( \ left ( C \ right ) \ ) là \ ( M \ left ( – 2 ; 1 \ right ). \ )
Chọn đáp án C.
Đáp án – Lời giải Câu hỏi 2 :Viết phương trình tiếp tuyến của đồ thị hàm số \ ( y = \ dfrac { { x + 3 } } { { x – 1 } } \ ), biết tiếp tuyến đó tạo với hai trục tọa độ một tam giác vuông cân .
- A\(y = – x + 6,\,\,y = – x – 2\)
- B\(y = – x – 6,\,\,y = – x – 2\)
- C\(y = x + 1,\,\,y = x + 6\)
- D\(y = x – 1,\,\,y = x – 6\)
Đáp án: A
Phương pháp giải :- Gọi \ ( M \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) là điểm thuộc đồ thị hàm số, viết phương trình tiếp tuyến của đồ thị hàm số tại \ ( M \ ) là : \ ( y = f ‘ \ left ( { { x_0 } } \ right ) \ left ( { x – { x_0 } } \ right ) + { y_0 } \, \, \, \ left ( d \ right ) \ ) .
– Xác định tọa độ những điểm \ ( A = Ox \ cap d, \, \, B = Oy \ cap d \ ) .
– Giải phương trình \ ( OA = OB \ ) tìm \ ( { x_0 } \ ), từ đó suy ra những phương trình tiếp tuyến thỏa mãn nhu cầu .Lời giải chi tiết cụ thể :TXĐ : \ ( D = \ mathbb { R } \ backslash \ left \ { 1 \ right \ } \ ). Ta có \ ( y ‘ = \ dfrac { { – 4 } } { { { { \ left ( { x – 1 } \ right ) } ^ 2 } } } \ ) .
Gọi \ ( M \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) là điểm thuộc đồ thị hàm số, phương trình tiếp tuyến của đồ thị hàm số tại \ ( M \ ) là :
\ ( y = \ dfrac { { – 4 } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } \ left ( { x – { x_0 } } \ right ) + \ dfrac { { { x_0 } + 3 } } { { { x_0 } – 1 } } \, \, \, \ left ( d \ right ) \ )
Gọi \ ( A = d \ cap Ox \ ) .
Cho \ ( y = 0 \ )
\ ( \ begin { array } { l } \ Rightarrow 0 = \ dfrac { { – 4 } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } \ left ( { x – { x_0 } } \ right ) + \ dfrac { { { x_0 } + 3 } } { { { x_0 } – 1 } } \ \ \ Leftrightarrow 0 = – 4 \ left ( { x – { x_0 } } \ right ) + \ left ( { { x_0 } + 3 } \ right ) \ left ( { { x_0 } – 1 } \ right ) \ \ \ Leftrightarrow 0 = – 4 x + 4 { x_0 } + x_0 ^ 2 + 2 { x_0 } – 3 \ \ \ Leftrightarrow x = \ dfrac { { x_0 ^ 2 + 6 { x_0 } – 3 } } { 4 } \ end { array } \ )
\ ( \ Rightarrow A \ left ( { \ dfrac { { x_0 ^ 2 + 6 { x_0 } – 3 } } { 4 } ; 0 } \ right ) \ ) \ ( \ Rightarrow OA = \ dfrac { { \ left | { x_0 ^ 2 + 6 { x_0 } – 3 } \ right | } } { 4 } \ ) .
Gọi \ ( B = d \ cap Oy \ ) .
Cho \ ( x = 0 \ ) .
\ ( \ begin { array } { l } \ Rightarrow y = \ dfrac { { 4 { x_0 } } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } + \ dfrac { { { x_0 } + 3 } } { { { x_0 } – 1 } } = \ dfrac { { 4 { x_0 } + \ left ( { { x_0 } + 3 } \ right ) \ left ( { { x_0 } – 1 } \ right ) } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } \ \ \, \, \, \, \, \, \, \, \, = \ dfrac { { 4 { x_0 } + x_0 ^ 2 + 2 { x_0 } – 3 } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } = \ dfrac { { x_0 ^ 2 + 6 { x_0 } – 3 } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } \ end { array } \ )
\ ( \ Rightarrow B \ left ( { 0 ; \ dfrac { { x_0 ^ 2 + 6 { x_0 } – 3 } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } } \ right ) \ Rightarrow OB = \ dfrac { { \ left | { x_0 ^ 2 + 6 { x_0 } – 3 } \ right | } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } \ ) .
Vì tam giác \ ( OAB \ ) vuông cân tại \ ( O \ ) nên \ ( OA = OB \ ) .
\ ( \ begin { array } { l } \ Leftrightarrow \ dfrac { { \ left | { x_0 ^ 2 + 6 { x_0 } – 3 } \ right | } } { 4 } = \ dfrac { { \ left | { x_0 ^ 2 + 6 { x_0 } – 3 } \ right | } } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } \ \ \ Leftrightarrow \ left | { x_0 ^ 2 + 6 { x_0 } – 3 } \ right | \ left ( { \ dfrac { 1 } { 4 } – \ dfrac { 1 } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } } \ right ) = 0 \ \ \ Leftrightarrow \ dfrac { 1 } { 4 } – \ dfrac { 1 } { { { { \ left ( { { x_0 } – 1 } \ right ) } ^ 2 } } } = 0 \ end { array } \ )
( Do \ ( A \ ne B \ ) nên \ ( x_0 ^ 2 + 6 { x_0 } – 3 \ ne 0 \ ) )
\ ( \ Leftrightarrow { \ left ( { { x_0 } – 1 } \ right ) ^ 2 } = 4 \ Leftrightarrow \ left [ \ begin { array } { l } { x_0 } – 1 = 2 \ \ { x_0 } – 1 = – 2 \ end { array } \ right. \ ) \ ( \ Leftrightarrow \ left [ \ begin { array } { l } { x_0 } = 3 \ \ { x_0 } = – 1 \ end { array } \ right. \, \, \ left ( { tm } \ right ) \ ) .
Với \ ( { x_0 } = 3 \ ) \ ( \ Rightarrow \ ) Phương trình tiếp tuyến : \ ( y = – 1 \ left ( { x – 3 } \ right ) + 3 \ Leftrightarrow y = – x + 6 \ ) .
Với \ ( { x_0 } = – 1 \ ) \ ( \ Rightarrow \ ) Phương trình tiếp tuyến : \ ( y = – 1 \ left ( { x + 1 } \ right ) – 1 \ Leftrightarrow y = – x – 2 \ ) .
Chọn A.
Đáp án – Lời giải Câu hỏi 3 :Gọi \ ( S \ ) là tập hợp những giá trị nguyên của \ ( m \ ) để mọi tiếp tuyến của đồ thị hàm số \ ( y = { x ^ 3 } – \ left ( { m – 1 } \ right ) { x ^ 2 } + \ left ( { m – 1 } \ right ) x + 5 \ ) đều có thông số góc dương. Số thành phần của tập \ ( S \ ) là :
- AVô số
- B\(4\)
- C\(3\)
- D\(2\)
Đáp án: D
Phương pháp giải :- Gọi \ ( M \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) thuộc đồ thị hàm số. Hệ số góc của tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm \ ( M \ ) là \ ( k = y ‘ \ left ( { { x_0 } } \ right ) \ ) .
– Xét dấu tam thức bậc hai : \ ( a { x ^ 2 } + bx + c > 0 \, \, \ forall x \ in \ mathbb { R } \ Leftrightarrow \ left \ { \ begin { array } { l } a > 0 \ \ \ Delta < 0 \ end { array } \ right. \ ) .Lời giải chi tiết cụ thể :Gọi \ ( M \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) thuộc đồ thị hàm số .
Ta có \ ( y ' = 3 { x ^ 2 } - 2 \ left ( { m - 1 } \ right ) x + m - 1 \ ) .
Suy ra thông số góc của tiếp tuyến của đồ thị hàm số tại điểm \ ( M \ ) là \ ( k = y ' \ left ( { { x_0 } } \ right ) = 3 x_0 ^ 2 - 2 \ left ( { m - 1 } \ right ) { x_0 } + m - 1 \ ) .
Theo bài ra ta có :
\ ( \ begin { array } { l } k > 0 \, \, \ forall x \ in \ mathbb { R } \ \ \ Leftrightarrow 3 x_0 ^ 2 – 2 \ left ( { m – 1 } \ right ) { x_0 } + m – 1 > 0 \, \, \ forall x \ in \ mathbb { R } \ \ \ Leftrightarrow \ left \ { \ begin { array } { l } 3 > 0 \, \, \ left ( { luon \, \, dung } \ right ) \ \ \ Delta ‘ = { \ left ( { m – 1 } \ right ) ^ 2 } – 3 \ left ( { m – 1 } \ right ) < 0 \, \ end { array } \ right. \, \ forall x \ in \ mathbb { R } \ \ \ Leftrightarrow { m ^ 2 } - 2 m + 1 - 3 m + 3 < 0 \ \ \ Leftrightarrow { m ^ 2 } - 5 m + 4 < 0 \ \ \ Leftrightarrow 1 < m < 4 \ end { array } \ )
Mà \ ( m \ in \ mathbb { Z } \ Rightarrow S = \ left \ { { 2 ; 3 } \ right \ } \ ) .
Vậy tập hợp \ ( S \ ) có 2 thành phần .
Chọn D.
Đáp án – Lời giải Câu hỏi 4 :Tìm số tiếp tuyến của đồ thị hàm số \ ( y = 4 { x ^ 3 } – 6 { x ^ 2 } + 1 \ ), biết tiếp tuyến đó đi qua điểm \ ( M \ left ( { – 1 ; – 9 } \ right ). \ )
- A\(1.\)
- B\(2.\)
- C\(3.\)
- D\(0.\)
Đáp án: B
Phương pháp giải :- Gọi tiếp điểm là \ ( { A_0 } \ left ( { { x_0 } ; { y_0 } } \ right ) \ ). Viết phương trình tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm \ ( A \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) là : \ ( y = f ‘ \ left ( { { x_0 } } \ right ). \ left ( { x – { x_0 } } \ right ) + { y_0 } \ ) .
– Cho tiếp tuyến vừa viết được đi qua \ ( M \ left ( { – 1 ; – 9 } \ right ) \ ), giải phương trình tìm \ ( { x_0 } \ ) .
– Số tiếp tuyến cần tìm là số nghiệm \ ( { x_0 } \ ) tìm được .Lời giải chi tiết cụ thể :Gọi tiếp điểm là \ ( { A_0 } \ left ( { { x_0 } ; { y_0 } } \ right ) \ ). Ta có : \ ( { y_0 } = 4 x_0 ^ 3 – 6 x_0 ^ 2 + 1 \ )
Ta có : \ ( y ‘ = 12 { x ^ 2 } – 12 x \ Rightarrow y ‘ \ left ( { { x_0 } } \ right ) = 12 x_0 ^ 2 – 12 { x_0 } \ )
Phương trình tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm \ ( { M_0 } \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) là :
\ ( y = \ left ( { 12 x_0 ^ 2 – 12 { x_0 } } \ right ). \ left ( { x – { x_0 } } \ right ) + 4 x_0 ^ 3 – 6 x_0 ^ 2 + 1 \ ) ( d )
Theo bài ra ta có : \ ( M \ left ( { – 1 ; – 9 } \ right ) \ in d \ Rightarrow \ ) \ ( – 9 = \ left ( { 12 x_0 ^ 2 – 12 { x_0 } } \ right ). \ left ( { – 1 – { x_0 } } \ right ) + 4 x_0 ^ 3 – 6 x_0 ^ 2 + 1 \ ) .
\(\begin{array}{l} \Leftrightarrow – 9 = – 12x_0^2 – 12x_0^3 + 12{x_0} + 12x_0^2 + 4x_0^3 – 6x_0^2 + 1\\ \Leftrightarrow 8x_0^3 + 6x_0^2 – 12{x_0} – 10 = 0 \Leftrightarrow \left[ \begin{array}{l}{x_0} = – 1\\{x_0} = \dfrac{5}{4}\end{array} \right.\end{array}\)
Dễ dàng kiểm tra, mỗi giá trị \ ( { x_0 } \ ) tìm được cho ta đúng một phương trình tiếp tuyến, hai đường tiếp tuyến tìm được là phân biệt .
Vậy qua \ ( M \ left ( { – 1 ; – 9 } \ right ) \ ) kẻ được hai tiếp tuyến đến đồ thị hàm số .
Chọn B.
Đáp án – Lời giải Câu hỏi 5 :Cho hàm số \ ( y = f \ left ( x \ right ) \ ) xác lập liên tục trên \ ( \ mathbb { R } \ ) và \ ( f ‘ \ left ( { – 2 } \ right ) = 3 \ ). Tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại tiếp điểm có hoành độ \ ( x = – 2 \ ) là đường thẳng \ ( 3 x + 4 \ ). Đặt \ ( g \ left ( x \ right ) = { \ left [ { f \ left ( x \ right ) } \ right ] ^ 2 } \ ), khi đó giá trị của \ ( g ‘ \ left ( – 2 \ right ) \ ) là
- A\( – 4\)
- B\( – 12\)
- C\(12\)
- D\(6\)
Đáp án: B
Phương pháp giải :- Tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm \ ( x = a \ ) có phương trình là : \ ( y = f ‘ \ left ( a \ right ) \ left ( { x – a } \ right ) + f \ left ( a \ right ). \ ) .
– Tính \ ( f \ left ( { – 2 } \ right ) \ ) và đạo hàm của hàm số \ ( y = g \ left ( x \ right ) \ ) để tính \ ( g ‘ \ left ( { – 2 } \ right ). \ )Lời giải cụ thể :Phương trình tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm \ ( x = – 2 \ ) là :
\ ( \ begin { array } { l } y = f ‘ \ left ( { – 2 } \ right ). \ left ( { x + 2 } \ right ) + f \ left ( { – 2 } \ right ) \ \ \ Leftrightarrow 3 x + 4 = 3. \ left ( { x + 2 } \ right ) + f \ left ( { – 2 } \ right ) \ \ \ Rightarrow f \ left ( { – 2 } \ right ) = – 2 \ end { array } \ )
Ta có :
\ ( \ begin { array } { l } g \ left ( x \ right ) = { \ left [ { f \ left ( x \ right ) } \ right ] ^ 2 } \ Rightarrow g ‘ \ left ( x \ right ) = 2. f ‘ \ left ( x \ right ). f \ left ( x \ right ) \ \ \ Rightarrow g ‘ \ left ( { – 2 } \ right ) = 2. f ‘ \ left ( { – 2 } \ right ). f \ left ( { – 2 } \ right ) = 2.3. \ left ( { – 2 } \ right ) = – 12. \ end { array } \ )
Vậy \ ( g ‘ \ left ( { – 2 } \ right ) = – 12. \ )
Chọn B.
Đáp án – Lời giải Câu hỏi 6 :Tiếp tuyến bất kỳ của đồ thị hàm số \ ( y = \ dfrac { { 4 x – 3 } } { { 2 x + 1 } } \ ) cùng với 2 tiệm cận tạo thành tam giác có diện tích quy hoạnh bằng :
- A\(4\).
- B\(7\).
- C\(5\).
- D\(6\)
Đáp án: C
Phương pháp giải :
Phương trình tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \(M\left( {{x_0};{y_0}} \right)\)là: \(y = f’\left( {{x_0}} \right).\left( {x – {x_0}} \right) + {y_0}\).
Lời giải cụ thể :Đồ thị hàm số \ ( y = \ dfrac { { 4 x – 3 } } { { 2 x + 1 } } \ ) \ ( \ left ( C \ right ) \ ) có hai tiệm cận là : \ ( x = – \ dfrac { 1 } { 2 }, \, y = 2 \ ), giao điểm của hai tiệm cận là : \ ( I \ left ( { – \ dfrac { 1 } { 2 } ; 2 } \ right ) \ )
Lấy \ ( M \ left ( { { x_0 } ; { y_0 } } \ right ) \ in \ left ( C \ right ) \ Rightarrow { y_0 } = \ dfrac { { 4 { x_0 } – 3 } } { { 2 { x_0 } + 1 } } \, \, \ left ( { { x_0 } \ ne – \ dfrac { 1 } { 2 } } \ right ) \ ), \ ( y ‘ \ left ( { { x_0 } } \ right ) = \ dfrac { { 10 } } { { { { \ left ( { 2 { x_0 } + 1 } \ right ) } ^ 2 } } } \ )
PTTT của \(\left( C \right)\) tại điểm M là: \(y = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( {x – {x_0}} \right) + \dfrac{{4{x_0} – 3}}{{2{x_0} + 1}}\,\,\left( d \right)\)
Cho \(x = – \dfrac{1}{2} \Rightarrow \)\(y = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( { – \dfrac{1}{2} – {x_0}} \right) + \dfrac{{4{x_0} – 3}}{{2{x_0} + 1}}\)\( = \dfrac{{ – 5}}{{2{x_0} + 1}} + \dfrac{{4{x_0} – 3}}{{2{x_0} + 1}} = \dfrac{{4{x_0} – 8}}{{2{x_0} + 1}}.\)
\( \Rightarrow \)Giao điểm của d và TCĐ của \(\left( C \right)\) là: \(A\left( { – \dfrac{1}{2};\dfrac{{4{x_0} – 8}}{{2{x_0} + 1}}} \right)\)\( \Rightarrow IA = \left| {\dfrac{{4{x_0} – 8}}{{2{x_0} + 1}} – 2} \right| = \left| {\dfrac{{10}}{{2{x_0} + 1}}} \right|.\)
Cho \ ( y = 2 \ ) ta có :
\(\begin{array}{l}2 = \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( {x – {x_0}} \right) + \dfrac{{4{x_0} – 3}}{{2{x_0} + 1}}\\ \Leftrightarrow \dfrac{{10}}{{{{\left( {2{x_0} + 1} \right)}^2}}}.\left( {x – {x_0}} \right) = \dfrac{5}{{2{x_0} + 1}}\\ \Leftrightarrow x – {x_0} = \dfrac{{2{x_0} + 1}}{2} \Leftrightarrow x = \dfrac{{4{x_0} + 1}}{2}\end{array}\)
\ ( \ Rightarrow \ ) Giao điểm của d và TCN của \ ( \ left ( C \ right ) \ ) là : \ ( B \ left ( { \ dfrac { { 4 { x_0 } + 1 } } { 2 } ; 2 } \ right ) \ ) \ ( \ Rightarrow IB = \ left | { \ dfrac { { 4 { x_0 } + 1 } } { 2 } + \ dfrac { 1 } { 2 } } \ right | = \ left | { 2 { x_0 } + 1 } \ right |. \ )
Diện tích tam giác tạo thành là : \ ( S = \ dfrac { 1 } { 2 }. IA.IB = \ dfrac { 1 } { 2 }. \ left | { \ dfrac { { 10 } } { { 2 { x_0 } + 1 } } } \ right |. \ left | { 2 { x_0 } + 1 } \ right | = 5 \ ) .
Chọn C.
Đáp án – Lời giải Câu hỏi 7 :Cho hàm số \ ( y = { x ^ 3 } – 3 x + 1 \ ) có đồ thị \ ( \ left ( C \ right ) \ ). Xét những điểm \ ( A, \, \, B \ ) đổi khác thuộc \ ( \ left ( C \ right ) \ ) sao cho tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại \ ( A, \, \, B \ ) song song với nhau. Gọi \ ( E, \, \, F \ ) lần lượt là giao điểm của những tiếp tuyến tại A và B với trục tung. Có bao nhiêu điểm \ ( A \ ) có hoành độ là số nguyên dương sao cho \ ( EF \ le 2020 \ ) ?
- A\(10\).
- B\(11\).
- C\(8\).
- D\(7\).
Đáp án: D
Phương pháp giải :- Giả sử hoành độ của \ ( A, \, \, B \ ) lần lượt là \ ( a, \, \, b \, \, \ left ( { a \ ne b } \ right ) \ ). Dựa vào giả thiết tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại \ ( A, \, \, B \ ) song song với nhau, tức là \ ( y ‘ \ left ( a \ right ) = y ‘ \ left ( b \ right ) \ ), rút \ ( b \ ) theo \ ( a \ ) .
– Viết phương trình tiếp tuyến tại \ ( A, \, \, B \ ) theo tham số \ ( a \ ) .
– Xác định tọa độ những điểm \ ( E, \, \, F \ ) theo tham số \ ( a \ ) .
– Tính \ ( EF \ ) theo tham số \ ( a \ ), sử dụng giả thiết \ ( EF \ le 2020 \ ) tìm khoảng chừng giá trị của \ ( a \ ), từ đó tìm những số nguyên dương \ ( a \ ) thỏa mãn nhu cầu điều kiện kèm theo tìm được .Lời giải cụ thể :TXĐ : \ ( D = \ mathbb { R } \ ). Ta có : \ ( y ‘ = 3 { x ^ 2 } – 3 \ ) .
Giả sử hoành độ của \ ( A, \, \, B \ ) lần lượt là \ ( a, \, \, b \, \, \ left ( { a \ ne b } \ right ) \ ). Do tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại \ ( A, \, \, B \ ) song song với nhau nên
\ ( y ‘ \ left ( a \ right ) = y ‘ \ left ( b \ right ) \ Leftrightarrow 3 { a ^ 2 } – 3 = 3 { b ^ 2 } – 3 \ Leftrightarrow \ left [ \ begin { array } { l } a = b \, \, \, \, \, \ left ( { ktm } \ right ) \ \ a = – b \ end { array } \ right. \ )
Ta có : \ ( A \ left ( { a ; { a ^ 3 } – 3 a + 1 } \ right ), \, B \ left ( { – a ; – { a ^ 3 } + 3 a + 1 } \ right ) \ ) ( \ ( a \ in { \ mathbb { N } ^ * } \ ) ) .
+ ) Tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại \ ( A \ ) có phương trình :
\ ( y = \ left ( { 3 { a ^ 2 } – 3 } \ right ) \ left ( { x – a } \ right ) + { a ^ 3 } – 3 a + 1 \ Leftrightarrow y = \ left ( { 3 { a ^ 2 } – 3 } \ right ) x – 2 { a ^ 3 } + 1 \ )
Giao điểm của tiếp tuyến này với \ ( Oy \ ) là điểm \ ( E \ left ( { 0 ; – 2 { a ^ 3 } + 1 } \ right ) \ ) .
+ ) Tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại \ ( B \ ) có phương trình :
\ ( y = \ left ( { 3 { a ^ 2 } – 3 } \ right ) \ left ( { x + a } \ right ) – { a ^ 3 } + 3 a + 1 \ Leftrightarrow y = \ left ( { 3 { a ^ 2 } – 3 } \ right ) x + 2 { a ^ 3 } + 1 \ )
Giao điểm của tiếp tuyến này với \ ( Oy \ ) là điểm \ ( F \ left ( { 0 ; 2 { a ^ 3 } + 1 } \ right ) \ ) .
\ ( \ Rightarrow EF = \ left | { 4 { a ^ 3 } } \ right | = 4 { a ^ 3 } \, \, \ Rightarrow 4 { a ^ 3 } < 2020 \, \ Rightarrow a < \ sqrt [ 3 ] { { 505 } } \ approx 7,96 \ )
Mà \ ( a \ in { \ mathbb { N } ^ * } \ ) \ ( \ Rightarrow a \ in \ left \ { { 1 ; 2 ; ... ; 7 } \ right \ } \ ) .
Vậy có 7 giá trị của \ ( a \ ) thỏa mãn nhu cầu nhu yếu bài toán .
Chọn D.
Đáp án – Lời giải Câu hỏi 8 :Cho hàm số \ ( y = \ dfrac { { 2 x – 2 } } { { x – 2 } } \ ) có đồ thị là \ ( \ left ( C \ right ) \ ), \ ( M \ ) là điểm thuộc \ ( \ left ( C \ right ) \ ) sao cho tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại \ ( M \ ) cắt hai đường tiệm cận của \ ( \ left ( C \ right ) \ ) tại hai điểm \ ( A \ ), \ ( B \ ) thỏa mãn nhu cầu \ ( AB = 2 \ sqrt 5 \ ). Gọi \ ( S \ ) là tổng những hoành độ của tổng thể những điểm \ ( M \ ) thỏa mãn nhu cầu bài toán. Tìm giá trị của \ ( S \ ) .
- A\(6\)
- B\(5\)
- C\(8\)
- D\(7\)
Đáp án: C
Phương pháp giải :- Tìm 2 đường tiệm cận của đồ thị hàm số .
– Gọi \ ( M \ left ( { m ; \, \ dfrac { { 2 m – 2 } } { { m – 2 } } } \ right ) \ ) thuộc đồ thị hàm số. Viết phương trình tiếp tuyến của đồ thị hàm số tại \ ( M \ ) .
– Tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm có hoành độ \ ( x = { x_0 } \ ) là \ ( y = f ‘ \ left ( { { x_0 } } \ right ) \ left ( { x – { x_0 } } \ right ) + f \ left ( { { x_0 } } \ right ) \ ) .
– Tìm giao điểm \ ( A, \, \, B \ ) của tiếp tuyến với 2 đường tiệm cận .
– Tính độ dài đoạn thẳng \ ( AB : \ ) \ ( AB = \ sqrt { { { \ left ( { { x_B } – { x_A } } \ right ) } ^ 2 } + { { \ left ( { { y_B } – { y_A } } \ right ) } ^ 2 } } \ ) .
– Giải phương trình tìm \ ( m \ ), từ đó tính \ ( S \ ) .Lời giải chi tiết cụ thể :TXĐ : \ ( D = \ mathbb { R } \ backslash \ left \ { 2 \ right \ } \ ). Đồ thị hàm số có hai đường tiệm cận là \ ( x = 2 \ ) và \ ( y = 2 \ ) .
Ta có \ ( y ‘ = \ dfrac { { – 2 } } { { { { \ left ( { x – 2 } \ right ) } ^ 2 } } } \ ). Gọi \ ( M \ left ( { m ; \, \ dfrac { { 2 m – 2 } } { { m – 2 } } } \ right ) \ ) thuộc đồ thị hàm số .
Phương trình tiếp tuyến \ ( d \ ) của \ ( \ left ( C \ right ) \ ) tại \ ( M \ ) : \ ( y = \ dfrac { { – 2 } } { { { { \ left ( { m – 2 } \ right ) } ^ 2 } } } \ left ( { x – m } \ right ) + \ dfrac { { 2 m – 2 } } { { m – 2 } } \ ) .
Cho \ ( x = 2 \ Rightarrow y = \ dfrac { { – 2 } } { { { { \ left ( { m – 2 } \ right ) } ^ 2 } } } \ left ( { 2 – m } \ right ) + \ dfrac { { 2 m – 2 } } { { m – 2 } } \ ) \ ( \ Leftrightarrow y = \ dfrac { 2 } { { m – 2 } } + \ dfrac { { 2 m – 2 } } { { m – 2 } } = \ dfrac { { 2 m } } { { m – 2 } } \ ) .
\ ( \ Rightarrow \ ) Giao điểm của \ ( d \ ) và đường thẳng \ ( x = 2 \ ) là \ ( A \ left ( { 2 ; \, \ dfrac { { 2 m } } { { m – 2 } } } \ right ) \ ) .
Cho \ ( y = 2 \ Rightarrow \ dfrac { { – 2 } } { { { { \ left ( { m – 2 } \ right ) } ^ 2 } } } \ left ( { x – m } \ right ) + \ dfrac { { 2 m – 2 } } { { m – 2 } } = 2 \ ) .
\ ( \ begin { array } { l } \ Leftrightarrow – 2 \ left ( { x – m } \ right ) + \ left ( { 2 m – 2 } \ right ) \ left ( { m – 2 } \ right ) = 2 { \ left ( { m – 2 } \ right ) ^ 2 } \ \ \ Leftrightarrow – 2 x + 2 m + 2 { m ^ 2 } – 6 m + 4 = 2 { m ^ 2 } – 8 m + 8 \ \ \ Leftrightarrow 2 x = 4 m – 4 \ Leftrightarrow x = 2 m – 2 \ end { array } \ )
\ ( \ Rightarrow \ ) Giao điểm của \ ( d \ ) và đường thẳng \ ( y = 2 \ ) là \ ( B \ left ( { 2 m – 2 ; \, 2 } \ right ) \ ) .
Ta có : \ ( AB = 2 \ sqrt 5 \ Leftrightarrow { \ left ( { 2 m – 4 } \ right ) ^ 2 } + { \ left ( { 2 – \ dfrac { { 2 m } } { { m – 2 } } } \ right ) ^ 2 } = 20 \ )
\ ( \ begin { array } { l } \ Leftrightarrow 4 { \ left ( { m – 2 } \ right ) ^ 2 } + \ dfrac { { 16 } } { { { { \ left ( { m – 2 } \ right ) } ^ 2 } } } = 20 \ \ \ Leftrightarrow { \ left ( { m – 2 } \ right ) ^ 4 } – 5 { \ left ( { m – 2 } \ right ) ^ 2 } + 4 = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } { \ left ( { m – 2 } \ right ) ^ 2 } = 1 \ \ { \ left ( { m – 2 } \ right ) ^ 2 } = 4 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } m = 3 \ \ m = 1 \ \ m = 4 \ \ m = 0 \ end { array } \ right. \ end { array } \ )
Vậy \ ( S = 3 + 1 + 4 + 0 = 8 \ ) .
Chọn C.
Đáp án – Lời giải Câu hỏi 9 :Cho hàm số \ ( y = \ dfrac { { x + b } } { { ax – 2 } } \ ) \ ( \ left ( { ab \ ne – 2 } \ right ) \ ). Biết rằng \ ( a \ ) và \ ( b \ ) là những giá trị thỏa mãn nhu cầu tiếp tuyến của đồ thị hàm số tại điểm \ ( A \ left ( { 1 ; \, \, – 2 } \ right ) \ ) song song với đường thẳng \ ( d : \, \, 3 x + y – 4 = 0 \ ). Khi đó giá trị của \ ( a – 3 b \ ) bằng :
- A\( – 2\)
- B\(4\)
- C\( – 1\)
- D\(5\)
Đáp án: A
Phương pháp giải :- Tiếp tuyến của đồ thị hàm số tại \ ( A \ left ( { 1 ; \, \, – 2 } \ right ) \ ) song song với đường thẳng \ ( d : \, \, 3 x + y – 4 = 0 \ ) nên \ ( y ‘ \ left ( 1 \ right ) = – 3 \ ) .
– Điểm \ ( A \ left ( { 1 ; – 2 } \ right ) \ ) thuộc đồ thị hàm số nên thay điểm \ ( A \ ) vào hàm số .
– Giải hệ 2 phương trình bằng giải pháp thế, tìm \ ( a, \, \, b \ ) và tính \ ( a – 3 b \ ) .Lời giải chi tiết cụ thể :Ta có \ ( y ‘ = \ dfrac { { – 2 – ab } } { { { { \ left ( { ax – 2 } \ right ) } ^ 2 } } } \ Rightarrow y ‘ \ left ( 1 \ right ) = \ dfrac { { – 2 – ab } } { { { { \ left ( { a – 2 } \ right ) } ^ 2 } } } \ ) .
Do tiếp tuyến song song với đường thẳng \ ( d : \, \, 3 x + y – 4 = 0 \ ) nên : \ ( y ‘ \ left ( 1 \ right ) = – 3 \ Leftrightarrow \ dfrac { { – 2 – ab } } { { { { \ left ( { a – 2 } \ right ) } ^ 2 } } } = – 3 \ ) .
Mặt khác \ ( A \ left ( { 1 ; – 2 } \ right ) \ ) thuộc đồ thị hàm số nên \ ( – 2 = \ dfrac { { 1 + b } } { { a – 2 } } \ ) \ ( \ Leftrightarrow b = – 2 a + 3 \ ) .
Khi đó ta có :
\ ( \ begin { array } { l } \ dfrac { { – 2 – ab } } { { { { \ left ( { a – 2 } \ right ) } ^ 2 } } } = – 3 \ Leftrightarrow – 2 – a \ left ( { – 2 a + 3 } \ right ) = – 3 { a ^ 2 } + 12 a – 12 \, \, \ left ( { a \ ne 2 } \ right ) \ \ \ Leftrightarrow 5 { a ^ 2 } – 15 a + 10 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } a = 2 \, \, \, \, \ left ( { ktm } \ right ) \ \ a = 1 \, \, \, \, \, \, \ left ( { tm } \ right ) \ end { array } \ right. \ end { array } \ ) .
Với \ ( a = 1 \ Rightarrow b = 1 \ Rightarrow a – 3 b = – 2 \ ) .
Chọn A.
Đáp án – Lời giải Câu hỏi 10 :Cho hàm số \ ( y = { x ^ 3 } – 3 { x ^ 2 } + 2 \ ) có đồ thị \ ( \ left ( C \ right ) \ ). Giả sử đường thẳng \ ( \ left ( d \ right ) : \, \, y = ax + b \ ) là tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại điểm có hoành độ dương. Tính \ ( a – b \ ) biết rằng \ ( \ left ( d \ right ) \ ) cắt trục hoành và trục tung lần lượt tại \ ( A \ ) và \ ( B \ ) sao cho \ ( OB = 9OA \ ) .
- A\(10\)
- B\(34\)
- C\( – 2\)
- D\( – 16\)
Đáp án: B
Phương pháp giải :
– Gọi \ ( A \ left ( { m ; 0 } \ right ) = d \ cap Ox \, \, \ left ( { m \ ne 0 } \ right ) \ ), xác lập tọa độ điểm \ ( B \ ) theo \ ( m \ ) .
– Viết phương trình đoạn chắn của đường thẳng \ ( d \ ) đi qua \ ( A, \, \, B \ ) .
– \ ( \ left ( d \ right ) : \, \, y = ax + b \ ) tiếp xúc với đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) thì \ ( a = f ‘ \ left ( x \ right ) \ ). Tìm \ ( x \ ) và viết phương trình tiếp tuyến sau đó suy ra \ ( a, \, \, b \ ) .Lời giải chi tiết cụ thể :Gọi \ ( A \ left ( { m ; 0 } \ right ) = d \ cap Ox \, \, \ left ( { m \ ne 0 } \ right ) \ ) \ ( \ Rightarrow OA = \ left | m \ right | \ ) .
\ ( \ Rightarrow OB = 9OA = 9 \ left | m \ right | \ ) \ ( \ Rightarrow B \ left ( { 0 ; 9 \ left | m \ right | } \ right ) = d \ cap Oy \ ) .
Khi đó ta có phương trình đoạn chắn của đường thẳng \ ( d \ ) là :
\ ( \ dfrac { x } { m } + \ dfrac { y } { { 9 \ left | m \ right | } } = 1 \ Leftrightarrow y = – \ dfrac { { 9 \ left | m \ right | } } { m } x + 9 \ left | m \ right | \ ) .
\ ( \ Rightarrow a = – \ dfrac { { 9 \ left | m \ right | } } { m } = \ pm 9 \ ), \ ( b = 9 \ left | m \ right | \ ) .
Vì \ ( d \ ) là tiếp tuyến của đồ thị hàm số \ ( y = { x ^ 3 } – 3 { x ^ 2 } + 2 \ ) nên \ ( y ‘ = 3 { x ^ 2 } – 6 x = \ pm 9 \ Leftrightarrow \ left [ \ begin { array } { l } x = 3 \ \ x = – 1 \ end { array } \ right. \ ) .
Theo giả thiết \ ( d \ ) là tiếp tuyến của \ ( \ left ( C \ right ) \ ) tại điểm có hoành độ dương nên \ ( d \ ) là tiếp tuyến tại điểm có hoành độ \ ( x = 3 \ ) .
\ ( \ Rightarrow y ‘ \ left ( 3 \ right ) = 9 ; \, \, y \ left ( 3 \ right ) = 2 \ ) .
Suy ra phương trình đường thẳng \ ( d \ ) là \ ( y = 9 \ left ( { x – 3 } \ right ) = 2 \ Leftrightarrow 9 x – 25 \ ) .
Vậy \ ( a = 9 ; \, \, b = – 25 \ Rightarrow a – b = 34 \ ) .
Chọn B.
Đáp án – Lời giải Câu hỏi 11 :Cho hàm số \ ( y = { x ^ 4 } – 2 { x ^ 2 } \ ) có đồ thị \ ( \ left ( S \ right ) \ ). Gọi \ ( A, \, \, B, \, \, C \ ) là những điểm phân biệt trên \ ( \ left ( S \ right ) \ ) có tiếp tuyến với \ ( \ left ( S \ right ) \ ) tại những điểm đó song song với nhau. Biết \ ( A, \, \, B, \, \, C \ ) cùng nằm trên một parabol \ ( \ left ( P \ right ) \ ) có đỉnh \ ( I \ left ( { \ frac { 1 } { 6 } ; { y_0 } } \ right ) \ ). Tìm \ ( { y_0 } \ ) ?
- A\({y_0} = \frac{1}{6}\)
- B\({y_0} = – \frac{1}{{36}}\)
- C\({y_0} = \frac{1}{{36}}\)
- D\({y_0} = – \frac{1}{6}\)
Đáp án: B
Phương pháp giải :Tiếp tuyến của đồ thị hàm số \ ( y = f \ left ( x \ right ) \ ) tại điểm có hoành độ \ ( x = { x_0 } \ ) là \ ( k = y ‘ \ left ( { { x_0 } } \ right ) \ ) .Lời giải cụ thể :\ ( y = { x ^ 4 } – 2 { x ^ 2 } \ Rightarrow y ‘ = 4 { x ^ 3 } – 4 x \ ) .
Giả sử những tiếp tuyến tại \ ( A, \, \, B, \, \, C \ ) có thông số góc cùng bằng \ ( k \ Rightarrow 4 { x ^ 3 } – 4 x = k \, \, \, \ left ( 1 \ right ) \ ) .
Ta có : \ ( { x ^ 4 } – 2 { x ^ 2 } = \ frac { 1 } { 4 } x \ left ( { 4 { x ^ 3 } – 4 x } \ right ) – { x ^ 2 } = \ frac { 1 } { 4 } xk – { x ^ 2 } \ ) .
Do đó ba điểm \ ( A, \, \, B, \, \, C \ ) thuộc đồ thị hàm số \ ( y = – { x ^ 2 } + \ frac { 1 } { 4 } kx \, \, \ left ( P \ right ) \ ) .
Theo giả thiết \ ( \ left ( P \ right ) \ ) có đỉnh \ ( I \ left ( { \ frac { 1 } { 6 } ; { y_0 } } \ right ) \ ) nên \ ( \ frac { { – \ frac { 1 } { 4 } k } } { { 2 \ left ( { – 1 } \ right ) } } = \ frac { 1 } { 6 } \ Leftrightarrow – \ frac { 1 } { 4 } k = – \ frac { 1 } { 3 } \ Leftrightarrow k = \ frac { 4 } { 3 } \ ) .
Khi đó \ ( \ left ( P \ right ) : \, \, y = – { x ^ 2 } + \ frac { 1 } { 3 } x \ ) .
Vậy \ ( { y_0 } = y \ left ( { \ frac { 1 } { 6 } } \ right ) = – { \ left ( { \ frac { 1 } { 6 } } \ right ) ^ 2 } + \ frac { 1 } { 3 }. \ frac { 1 } { 6 } = \ frac { 1 } { { 36 } } \ ) .
Chọn B.
Đáp án – Lời giải Câu hỏi 12 :Cho hàm số \ ( y = { x ^ 4 } + \ left ( { m – 2 } \ right ) { x ^ 2 } – 2 \ left ( { m + 2 } \ right ) x + m + 5 \ ) có đồ thị \ ( \ left ( { { C_m } } \ right ) \ ). Biết rằng mọi đường cong \ ( \ left ( { { C_m } } \ right ) \ ) đều tiếp xúc nhau tại 1 điểm. Viết phương trình tiếp tuyến chung của những đường cong \ ( \ left ( { { C_m } } \ right ) \ ) tại điểm đó ?
- A\(y = 0\)
- B\(y = – 4x + 4\)
- C\(y = – 4\)
- D\(y = – 4x – 4\)
Đáp án: B
Phương pháp giải :- Tìm điểm cố định và thắt chặt mà với mọi giá trị của \ ( m \ ) thì đồ thị hàm số luôn đi qua .
– Viết phương trình tiếp tuyến tại điểm đó .Lời giải cụ thể :Ta có :
\ ( \ begin { array } { l } \, \, \, \, \, \, \, y = { x ^ 4 } + \ left ( { m – 2 } \ right ) { x ^ 2 } – 2 \ left ( { m + 2 } \ right ) x + m + 5 \ \ \ Leftrightarrow y = \ left ( { { x ^ 4 } – 2 { x ^ 2 } – 4 x + 5 } \ right ) + m \ left ( { { x ^ 2 } – 2 x + 1 } \ right ) \ end { array } \ )
Để \ ( \ left ( { { C_m } } \ right ) \ ) luôn đi qua 1 điểm khi \ ( m \ ) biến hóa thì \ ( { x ^ 2 } – 2 x + 1 = 0 \ Leftrightarrow x = 1 \ )
Với \ ( x = 1 \ ) thì \ ( y = 0 \ ), suy ra đồ thị hàm số \ ( \ left ( { { C_m } } \ right ) \ ) luôn đi qua điểm cố định và thắt chặt \ ( A \ left ( { 1 ; 0 } \ right ) \ ) .
Ta có : \ ( y ‘ = f ‘ \ left ( x \ right ) = 4 { x ^ 3 } + 2 \ left ( { m – 2 } \ right ) x – 2 \ left ( { m + 2 } \ right ) \ ) .
\ ( \ Rightarrow f ‘ \ left ( 1 \ right ) = 4 + 2. \ left ( { m – 2 } \ right ). 1 – 2 \ left ( { m + 2 } \ right ) = 4 + 2 m – 4 – 2 m – 4 = – 4 \ )
Suy ra phương trình tiếp tuyến chung của những đường cong \ ( \ left ( { { C_m } } \ right ) \ ) tại điểm \ ( A \ left ( { 1 ; 0 } \ right ) \ ) là :
\ ( d : y = f ‘ \ left ( 1 \ right ) \ left ( { x – 1 } \ right ) + 0 = – 4 \ left ( { x – 1 } \ right ) = – 4 x + 4. \ )
Chọn B.
Đáp án – Lời giải Câu hỏi 13 :Cho hàm số \ ( y = – { x ^ 3 } + 3 { x ^ 2 } – 2 \ ) có đồ thị \ ( \ left ( C \ right ) \ ). Số tiếp tuyến với đồ thị \ ( \ left ( C \ right ) \ ) song song với đường thẳng \ ( y = – 9 x – 7 \ ) là :
- A3
- B1
- C0
- D2
Đáp án: B
Lời giải chi tiết cụ thể :\ ( \ left ( C \ right ) : \, \, y = – { x ^ 3 } + 3 { x ^ 2 } – 2 \ Rightarrow y ‘ = – 3 { x ^ 2 } + 6 x \ )
Tiếp tuyến của \ ( \ left ( C \ right ) \ ) song song với đường thẳng \ ( d : \, \, y = – 9 x – 7 \ ) .
\ ( \ Leftrightarrow \ ) Hệ số góc của tiếp tuyến bằng \ ( – 9 \ ) .
\ ( \ Leftrightarrow y ‘ \ left ( { { x_0 } } \ right ) = – 9 \ Leftrightarrow – 3 x_0 ^ 2 + 6 { x_0 } = – 9 \ Leftrightarrow \ left [ \ begin { array } { l } { x_0 } = 3 \ Rightarrow { y_0 } = – 2 \ \ { x_0 } = – 1 \ Rightarrow { y_0 } = 2 \ end { array } \ right. \ ) .
+ Tại tiếp điểm \ ( \ left ( { 3 ; – 2 } \ right ) \ Rightarrow \ ) Phương trình tiếp tuyến là : \ ( y = – 9 \ left ( { x – 3 } \ right ) – 2 = – 9 x + 25 \ ) .
+ Tại tiếp điểm \ ( \ left ( { – 1 ; 2 } \ right ) \ Rightarrow \ ) Phương trình tiếp tuyến là : \ ( y = – 9 \ left ( { x + 1 } \ right ) + 2 = – 9 x – 7 \ ) ( loại vì trùng \ ( d \ ) ) .
Chọn B
Đáp án – Lời giải Câu hỏi 14 :Tiếp tuyến của đường cong \ ( \ left ( C \ right ) : y = { x ^ 4 } + 2 { x ^ 2 } \ ) tại điểm \ ( M \ left ( { 1 ; 3 } \ right ) \ ) có phương trình là
- A\(y = 8x – 5.\)
- B\(y = 4x – 1.\)
- C\(y = – 8x + 5.\)
- D\(y = – 4x + 1.\)
Đáp án: A
Lời giải chi tiết cụ thể :Lập phương trình đường thẳng đi qua \ ( M \ left ( { 1 ; 3 } \ right ) \ ) :
\ ( y = k \ left ( { x – { x_0 } } \ right ) + { y_0 } \ Leftrightarrow y = k \ left ( { x – 1 } \ right ) + 3 \ )
Để đường thẳng đi qua \ ( M \ left ( { 1 ; 3 } \ right ) \ ) tiếp xúc với đồ thị \ ( \ left ( C \ right ) \ ) :
\ ( \ Rightarrow \ left \ { \ begin { array } { l } { x ^ 4 } + 2 { x ^ 2 } = k \ left ( { x – 1 } \ right ) + 3 \, \, \, \, \, \, \, \, \, \ left ( 1 \ right ) \ \ 4 { x ^ 3 } + 4 x = k \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left ( 2 \ right ) \ end { array } \ right. \ )
Thế ( 2 ) vào ( 1 ) ta có :
\ ( \ begin { array } { l } { x ^ 4 } + 2 { x ^ 2 } = \ left ( { 4 { x ^ 3 } + 4 x } \ right ) \ left ( { x – 1 } \ right ) + 3 \ Leftrightarrow { x ^ 4 } + 2 { x ^ 2 } = 4 { x ^ 4 } – 4 { x ^ 3 } + 4 { x ^ 2 } – 4 x + 3 \ \ \ Leftrightarrow 3 { x ^ 4 } – 4 { x ^ 3 } + 2 { x ^ 2 } – 4 x + 3 = 0 \ Leftrightarrow \ left ( { x – 1 } \ right ) \ left ( { 3 { x ^ 3 } – { x ^ 2 } + x – 3 } \ right ) = 0 \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ 3 { x ^ 3 } – { x ^ 2 } + x – 3 = 0 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ 3 \ left ( { { x ^ 3 } – 1 } \ right ) – x \ left ( { x – 1 } \ right ) = 0 \ end { array } \ right. \ \ \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ 3 \ left ( { x – 1 } \ right ) \ left ( { { x ^ 2 } – x + 1 } \ right ) – x \ left ( { x – 1 } \ right ) = 0 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ \ left ( { x – 1 } \ right ) \ left ( { 3 { x ^ 2 } – 4 x + 3 } \ right ) = 0 \ end { array } \ right. \ Leftrightarrow x = 1 \ end { array } \ )
Với \ ( x = 1 \ ) thì \ ( k = { 4.1 ^ 3 } + 4.1 = 8 \ ) .
Vậy phương trình tiếp tuyến cần tìm là : \ ( y = 8 \ left ( { x – 1 } \ right ) + 3 \ Leftrightarrow y = 8 x – 5 \ ) .
Chọn A
Đáp án – Lời giải Câu hỏi 15 :Cho hàm số \ ( y = { x ^ 3 } – 2 { x ^ 2 } + \ left ( { m – 1 } \ right ) x + 2 m \ ). Tìm \ ( m \ ) để từ điểm \ ( M \ left ( { 1 ; 2 } \ right ) \ ) kẻ được 2 tiếp tuyến đến đồ thị .
- A\(m \in \left\{ {\dfrac{4}{3};\dfrac{{109}}{{81}}} \right\}.\)
- B\(m \in \emptyset .\)
- C\(m = \dfrac{2}{3}.\)
- D\(m = \dfrac{{55}}{{81}}.\)
Đáp án: A
Lời giải chi tiết cụ thể :+ Lập phương trình đường thẳng đi qua \ ( M ( 1 ; 2 ) \ )
\ ( \ Rightarrow \ ) Phương trình đường thẳng có dạng : \ ( y = k \ left ( { x – { x_0 } } \ right ) + { y_0 } \ )
\ ( \ Leftrightarrow y = k \ left ( { x – 1 } \ right ) + 2 \ Leftrightarrow y = kx – k + 2 \ )
Đường thẳng qua M và tiếp xúc với Đồ thị
\ ( \ begin { array } { l } \ Rightarrow \ left \ { \ begin { array } { l } { x ^ 3 } – 2 { x ^ 2 } + ( m – 1 ) x + 2 m = kx – k + 2 \ \ 3 { x ^ 2 } – 4 x + ( m – 1 ) = k \ end { array } \ right. \ \ \ Leftrightarrow { x ^ 3 } – 2 { x ^ 2 } + mx – x + 2 m = 3 { x ^ 3 } – 4 { x ^ 2 } + mx – x – 3 { x ^ 2 } + 4 x – m + 1 + 2 \ \ \ Leftrightarrow 2 { x ^ 3 } – 5 { x ^ 2 } + 4 x + 3 = 3 m \, \, ( * ) \ end { array } \ )
Để kẻ được 2 tiếp tuyến đến đồ thị \ ( \ Rightarrow \ ) PT ( * ) phải có 2 nghiệm
Xét \ ( f \ left ( x \ right ) = 2 { x ^ 3 } – 5 { x ^ 2 } + 4 x + 3 \ )
\ ( f ‘ \ left ( x \ right ) = 6 { x ^ 2 } – 10 x + 4 = 0 \ Leftrightarrow \ left [ \ begin { array } { l } x = 1 \ \ x = \ dfrac { 2 } { 3 } \ end { array } \ right. \ )
BBT :
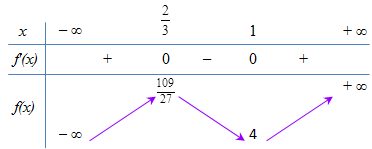
PT ( * ) có 2 nghiệm \ ( \ Rightarrow \ ) Đường thẳng \ ( y = 3 m \ ) phải cắt đồ thị tại 2 điểm \ ( \ Leftrightarrow \ left [ \ begin { array } { l } 3 m = \ dfrac { { 109 } } { { 27 } } \ \ 3 m = 4 \ end { array } \ right. \ Leftrightarrow \ left [ \ begin { array } { l } m = \ dfrac { { 109 } } { { 81 } } \ \ m = \ dfrac { 4 } { 3 } \ end { array } \ right .. \ )
Chọn A
Đáp án – Lời giải Câu hỏi 16 :Tìm trên trục tung những điểm mà từ đó kẻ được 3 tiếp tuyến tới đồ thị \ ( y = { x ^ 4 } – { x ^ 2 } + 1. \ )
- A\(\left( {0;1} \right)\)
- B\(\left( {0;\dfrac{1}{2}} \right)\)
- C\(\left( {0;\dfrac{3}{4}} \right)\)
- D\(\left( {0;\dfrac{1}{4}} \right)\)
Đáp án: A
Phương pháp giải :+ Gọi điểm trên trục tung là \ ( M \ left ( { 0 ; m } \ right ) \ )
+ Lập phương trình đường thẳng đi qua \ ( M \ left ( { 0 ; m } \ right ) \ )
\ ( \ Rightarrow \ ) Phương trình đường thẳng có dạng : \ ( y = k \ left ( { x – { x_0 } } \ right ) + { y_0 } \ Leftrightarrow y = k. \ left ( { x – 0 } \ right ) + m \ Leftrightarrow y = kx + m \ )
Đường thẳng tiếp tuyến qua \ ( M \ ) và tiếp xúc với đồ thị \ ( \ Rightarrow \ left \ { \ begin { array } { l } kx + m = { x ^ 4 } – { x ^ 2 } + 1 \, \, \, \, \ left ( 1 \ right ) \ \ k = 4 { x ^ 3 } – 2 x \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left ( 2 \ right ) \ end { array } \ right. \ )
Thế ( 2 ) vào ( 1 ) ta được :
\ ( \ begin { array } { l } \ Leftrightarrow m = – \ left ( { 4 { x ^ 3 } – 2 x } \ right ) x + { x ^ 4 } – { x ^ 2 } + 1 \ \ \ Leftrightarrow m = – 4 { x ^ 4 } + 2 { x ^ 2 } + { x ^ 4 } – { x ^ 2 } + 1 \ \ \ Leftrightarrow m = – 3 { x ^ 4 } + { x ^ 2 } + 1 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ left ( * \ right ) \ end { array } \ )
+ Để kẻ được 3 tiếp tuyến tới đồ thị thì PT ( * ) phải có 3 nghiệm .
Xét \ ( f \ left ( x \ right ) = – 3 { x_ { } } ^ 4 + { x_ { } } ^ 2 + 1 \ )
\ ( f ‘ \ left ( x \ right ) = – 12 { x_ { } } ^ 3 + 2 x = 0 \ Leftrightarrow \ left [ \ begin { array } { l } x = \ dfrac { { \ sqrt 6 } } { 6 } \ \ x = – \ dfrac { { \ sqrt 6 } } { 6 } \ \ x = 0 \ end { array } \ right. \ )
BBT :
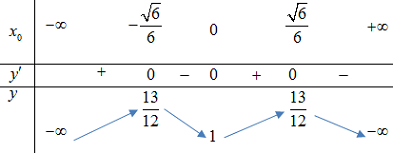
Để PT ( * ) có 3 nghiệm \ ( \ Rightarrow \ ) Đường thẳng \ ( y = m \ ) phải cắt đồ thị tại 3 điểm \ ( \ Leftrightarrow m = 1. \ )
Vậy điểm cần tìm là \ ( M \ left ( { 0 ; 1 } \ right ). \ )
Chọn A
Đáp án – Lời giải Câu hỏi 17 :Cho hàm số \ ( y = \ dfrac { { x + 2 } } { { x – 1 } } \ ) có đồ thị \ ( \ left ( C \ right ) \ ) và điểm \ ( A \ left ( { 0 ; \, a } \ right ) \ ). Hỏi có toàn bộ bao nhiêu giá trị nguyên của a trong đoạn \ ( \ left [ { – 2018 ; \, 2018 } \ right ] \ ) để từ điểm \ ( A \ ) kẻ được hai tiếp tuyến đến \ ( \ left ( C \ right ) \ ) sao cho hai tiếp điểm nằm về hai phía của trục hoành ?
- A\(2017\).
- B\(2020\).
- C\(2018\).
- D\(2019\).
Đáp án: C
Lời giải chi tiết cụ thể :Gọi phương trình đường thẳng qua \ ( A \ left ( { 0 ; \, a } \ right ) \ ) có dạng : \ ( y = k \ left ( { x – } \ right ) + a \ Leftrightarrow y = kx + a \ )
Đường thẳng qua A tiếp xúc với đồ thị \ ( \ Rightarrow \ left \ { \ begin { array } { l } \ dfrac { { x + 2 } } { { x – 1 } } = kx + a \, \, \, \, \, \, \, \, \, \ left ( 1 \ right ) \ \ \ dfrac { { – 3 } } { { { { \ left ( { x – 1 } \ right ) } ^ 2 } } } = k \, \, \, \, \, \, \, \, \, \, \, \, \, \ left ( 2 \ right ) \ end { array } \ right. \ )
Thế \ ( ( 2 ) \ ) vào \ ( ( 1 ) \ ) ta có : \ ( \ dfrac { { x + 2 } } { { x – 1 } } = \ dfrac { { – 3 x } } { { { { \ left ( { x – 1 } \ right ) } ^ 2 } } } + a \ )
\ ( \ begin { array } { l } \ Leftrightarrow { x ^ 2 } + x – 2 = – 3 x + a { x ^ 2 } – 2 ax + a \ \ \ Leftrightarrow \ left ( { 1 – a } \ right ) { x ^ 2 } + 2 \ left ( { 2 + a } \ right ) x – 2 – a = 0 \, \, \, \, \, \ left ( * \ right ) \ end { array } \ )
+ Để kẻ được 2 tiếp tuyến đến đồ thị có 2 tiếp điểm nằm 2 phía trục hoành .
\ ( \ Rightarrow \ ) Phương trình ( * ) phải có 2 nghiệm phân biệt \ ( { x_1 }, { x_2 } \ ) có tung độ trái dấu .
\ ( \ Rightarrow \ ) \ ( \ left \ { \ begin { array } { l } \ Delta > 0 \ \ { y_1 }. { y_2 } < 0 \ \ a - 1 \ ne 0 \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { l } \ Delta > 0 \ \ \ dfrac { { { x_1 } + 2 } } { { { x_1 } – 1 } }. \ dfrac { { { x_2 } + 2 } } { { { x_2 } – 1 } } < 0 \ \ a \ ne 1 \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { l } \ Delta > 0 \, \, ( 1 ) \ \ \ dfrac { { { x_1 }. { x_2 } + 2 \ left ( { { x_1 } + { x_2 } } \ right ) + 4 } } { { { x_1 }. { x_2 } – \ left ( { { x_1 } + { x_2 } } \ right ) + 1 } } < 0 \, \, \, ( 2 ) \ \ a \ ne 1 \ end { array } \ right. \ )
\ ( ( 1 ) \ Leftrightarrow \ Delta = 4 { \ left ( { 2 + a } \ right ) ^ 2 } - 4 \ left ( { 1 - a } \ right ). \ left ( { - 2 - a } \ right ) > 0 \ Leftrightarrow 12 a + 24 > 0 \ Leftrightarrow a > – 2 \ )
+ Theo Vi-et \ ( \ left \ { \ begin { array } { l } { x_1 } + { x_2 } = \ dfrac { { 2 \ left ( { 2 + a } \ right ) } } { { a – 1 } } \ \ { x_1 }. { x_2 } = \ dfrac { { 2 + a } } { { a – 1 } } \ end { array } \ right. \ )
\ ( \ left ( 2 \ right ) \ Leftrightarrow \ dfrac { { \ dfrac { { 2 + a } } { { a – 1 } } + \ dfrac { { 4 \ left ( { 2 + a } \ right ) } } { { a – 1 } } + 4 } } { { \ dfrac { { 2 + a } } { { a – 1 } } – \ dfrac { { 2 \ left ( { 2 + a } \ right ) } } { { a – 1 } } + 1 } } < 0 \ Leftrightarrow \ left [ \ begin { array } { l } \ dfrac { { - 2 } } { 3 } < a < 1 \ \ a > 1 \ end { array } \ right. \ )
Kết hợp ( 1 ) và ( 2 ) \ ( \ Rightarrow a \ in \ left ( { \ dfrac { { – 2 } } { 3 } ; 1 } \ right ) \ cup \ left ( { 1 ; + \ infty } \ right ) \ )
Mà \ ( a \ in \ left [ { – 2018 ; \, 2018 } \ right ] \ ) \ ( \ Rightarrow a \ in \ left ( { \ dfrac { { – 2 } } { 3 } ; 1 } \ right ) \ cup \ left ( { 1 ; 2018 } \ right ] \ ) \ ( \ Rightarrow \ ) Có 2018 giá trị a nguyên .
Chọn C
Đáp án – Lời giải Câu hỏi 18 :Điểm \ ( M \ ) trên đồ thị hàm số \ ( y = { x ^ 3 } – 3 { x ^ 2 } – 1 \ ) mà tiếp tuyến tại đó có thông số góc \ ( k \ ) bé nhất trong tổng thể những tiếp tuyến của đồ thị thì \ ( M \ ), \ ( k \ ) là :
- A\(M\left( {1;-3} \right)\), \(k = -3\).
- B\(M\left( {1;3} \right)\), \(k = -3\).
- C\(M\left( {1;-3} \right)\), \(k = 3\).
- D\(M\left( { – 1;-3} \right)\), \(k = -3\).
Đáp án: A
Lời giải cụ thể :\ ( y = { x ^ 3 } – 3 { x ^ 2 } – 1 \ Rightarrow y ‘ = 3 { x ^ 2 } – 6 x \ )
Để thông số góc \ ( { k_ { \ min } } \ Rightarrow y { ‘ _ { \ min } } \ )
\ ( \ begin { array } { l } y ‘ ‘ = 6 x – 6 = 0 \ Leftrightarrow x = 1 \ \ \ Leftrightarrow y { ‘ _ { \ min } } = y ‘ \ left ( 1 \ right ) = – 3 \ Rightarrow k = – 3 \ end { array } \ )
Tiếp tuyến tại M của đồ thị có thông số góc \ ( k \ ) bé nhất
\ ( \ Leftrightarrow 3 { x ^ 2 } – 6 x = – 3 \ Leftrightarrow x = 1 \ Rightarrow y = – 3 \ Rightarrow M \ left ( { 1 ; – 3 } \ right ) \ )
Chọn A.
Đáp án – Lời giải Câu hỏi 19 :Tìm tổng thể những giá trị của tham số m để đường thẳng \ ( d : \, \, y = 4 x + m \ ) tiếp xúc với đồ thị hàm số \ ( y = { x ^ 3 } + x + 2 \ ) .
- A\(m = 0;m = 4\)
- B\(m = 1;m = 2\)
- C\(m = 3\)
- DKhông có giá trị của m
Đáp án: A
Lời giải chi tiết cụ thể :Để \ ( d : y = 4 x + m \ ) tiếp xúc với \ ( y = { x ^ 3 } + x + 2 \ )
\ ( \ Leftrightarrow \ left \ { \ begin { array } { l } 4 x + m = { x ^ 3 } + x + 2 \ \ 4 = 3 { x ^ 2 } + 1 \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { l } { x ^ 3 } – 3 x + 2 – m = 0 \ \ \ left [ \ begin { array } { l } x = 1 \ \ x = – 1 \ end { array } \ right. \ end { array } \ right. \ )
Với \ ( x = 1 \ Rightarrow 1 – 3 + 2 – m = 0 \ Leftrightarrow m = 0 \ )
Với \ ( x = – 1 \ Rightarrow – 1 + 3 + 2 – m = 0 \ Leftrightarrow m = 4 \ )
Chọn A
Đáp án – Lời giải Câu hỏi 20 :Cho hàm số \ ( y = \ dfrac { { x – 2 } } { { x + 1 } } \ ) có đồ thị \ ( \ left ( C \ right ) \ ). Phương trình tiếp tuyến \ ( \ Delta \ ) của đồ thị hàm số \ ( \ left ( C \ right ) \ ) tạo với hai đường tiệm cận một tam giác có nửa đường kính đường tròn nội tiếp lớn nhất. Khi đó khoảng cách từ tâm đối xứng của \ ( \ left ( C \ right ) \ ) đến \ ( \ Delta \ ) bằng ?
- A \(\sqrt 3 \).
- B \(2\sqrt 6 \).
- C \(\sqrt 6 \).
- D \(2\sqrt 3 \).
Đáp án: C
Phương pháp giải :Đồ thị hàm số \ ( y = \ dfrac { { ax + b } } { { cx + d } }, \ left ( { ad – bc, c \ ne 0 } \ right ) \ ) có TCĐ : \ ( x = – \ dfrac { d } { c } \ ), TCN : \ ( y = \ dfrac { a } { c } \ ) và có tâm đối xứng là \ ( I \ left ( { – \ dfrac { d } { c } ; \ dfrac { a } { c } } \ right ) \ ) .Lời giải cụ thể :
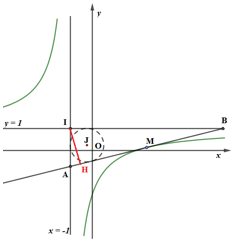
Đồ thị hàm số \ ( y = \ dfrac { { x – 2 } } { { x + 1 } } \ ) có TCĐ \ ( x = – 1 \ ), TCN : \ ( y = 1 \ ) và có tâm đối xứng là \ ( I \ left ( { – 1 ; 1 } \ right ) \ ) .
Gọi \ ( M \ left ( { { x_0 } ; { y_0 } } \ right ) \ ) là tiếp điểm ;
A, B lần lượt là giao điểm của tiếp tuyến \ ( \ Delta \ ) với TCĐ, TCN ;
J, r lần lượt là tâm và nửa đường kính của đường tròn nội tiếp tam giác IAB .
Phương trình tiếp tuyến \ ( \ Delta \ ) : \ ( y = y ‘ \ left ( { { x_0 } } \ right ). \ left ( { x – { x_0 } } \ right ) + { y_0 } \ Leftrightarrow y = \ dfrac { 3 } { { { { \ left ( { { x_0 } + 1 } \ right ) } ^ 2 } } }. \ left ( { x – { x_0 } } \ right ) + \ dfrac { { { x_0 } – 2 } } { { { x_0 } + 1 } } \ )
Cho \ ( x = – 1 \ Rightarrow y = \ dfrac { 3 } { { { { \ left ( { { x_0 } + 1 } \ right ) } ^ 2 } } }. \ left ( { – 1 – { x_0 } } \ right ) + \ dfrac { { { x_0 } – 2 } } { { { x_0 } + 1 } } = \ dfrac { { { x_0 } – 5 } } { { { x_0 } + 1 } } \ Rightarrow A \ left ( { – 1 ; \ dfrac { { { x_0 } – 5 } } { { { x_0 } + 1 } } } \ right ) \ Rightarrow IA = \ left | { \ dfrac { 6 } { { { x_0 } + 1 } } } \ right | \ )
Cho \ ( y = 1 \ Rightarrow 1 = \ dfrac { 3 } { { { { \ left ( { { x_0 } + 1 } \ right ) } ^ 2 } } }. \ left ( { x – { x_0 } } \ right ) + \ dfrac { { { x_0 } – 2 } } { { { x_0 } + 1 } } \ Leftrightarrow x = 2 { x_0 } + 1 \ Rightarrow B \ left ( { 2 { x_0 } + 1 ; 1 } \ right ) \ Rightarrow IB = 2 \ left | { { x_0 } + 1 } \ right | \ )
\ ( \ Rightarrow IA.IB = 12, \, \, \ forall { x_0 } \ ne – 1 \ )
\ ( { S_ { IAB } } = \ dfrac { 1 } { 2 } IA.IB = \ dfrac { 1 } { 2 } \ left ( { IA + IB + AB } \ right ). r \ )
\ ( \ Rightarrow r = \ dfrac { { IA.IB } } { { IA + IB + AB } } = \ dfrac { { IA.IB } } { { IA + IB + \ sqrt { I { A ^ 2 } + I { B ^ 2 } } } } \ )
\ ( = \ dfrac { { 12 } } { { IA + IB + \ sqrt { { { \ left ( { IA + IB } \ right ) } ^ 2 } – 24 } } } \ )
Ta có : \ ( IA + IB \ ge 2 \ sqrt { IA.IB } = 4 \ sqrt 3 \ ), dấu “ = ” xảy ra khi và chỉ khi \ ( IA = IB \ )
Đặt \ ( IA + IB = t, \, \, t \ ge 4 \ sqrt 3 \ ), ta có :
\ ( f \ left ( t \ right ) = t + \ sqrt { { t ^ 2 } – 24 } \ Rightarrow f ‘ \ left ( t \ right ) = 1 + \ dfrac { t } { { \ sqrt { { t ^ 2 } – 24 } } } > 0, \, \, \ forall t > 4 \ sqrt 3 \ )
\ ( \ Rightarrow \ ) Hàm số đồng biến trên \ ( \ left ( { 4 \ sqrt 3 ; + \ infty } \ right ) \ )
Ta có: \(f\left( {4\sqrt 3 } \right) = 8\sqrt 3 \)
\ ( \ Rightarrow f \ left ( t \ right ) \ ge 8 \ sqrt 3, \, \, \ forall t \ ge 4 \ sqrt 3 \ Rightarrow \ dfrac { { 12 } } { { f \ left ( t \ right ) } } \ le \ dfrac { { 12 } } { { 8 \ sqrt 3 } } = \ dfrac { { \ sqrt 3 } } { 2 }, \, \, \ forall t \ ge 4 \ sqrt 3 \ )
\ ( \ Rightarrow { r_ { \ max } } = \ dfrac { { \ sqrt 3 } } { 2 } \ ) khi và chỉ khi \ ( IA = IB = 2 \ sqrt 3 \ ) \ ( \ Rightarrow \ Delta IAB \ ) vuông cân tại I có \ ( d \ left ( { I ; \ Delta } \ right ) = IH = \ dfrac { { IA } } { { \ sqrt 2 } } = \ dfrac { { 2 \ sqrt 3 } } { { \ sqrt 2 } } = \ sqrt 6 \ )
Chọn: C
Đáp án – Lời giải
Source: http://wp.ftn61.com
Category: Hỏi Đáp



Để lại một bình luận