3 cách giải phương trình bậc 2 cực đơn giản, chính xác 100%

Chúng tôi sẽ hướng dẫn các bạn giải phương trình bậc 2 như phương trình bậc 2 số phức, phương trình bậc 2 1 ẩn, phương trình bậc 2 2 ẩn, cách tính delta với các phương pháp khác nhau như công thức nghiệm của phương trình bậc 2, sử dụng định lý Viet, tính nhẩm,..chi tiết trong bài viết dưới đây.

Phương trình bậc 2 là gì

?

Phương trình bậc 2 là phương trình có dạng ax2 + bx + c = 0 ( a ≠ 0 ) ( 1 ). Trong đó :

• x: là ẩn số
• a, b, c: là các số đã biết gắn với biến x sao cho: a ≠ 0.

Cách giải phương trình bậc 2 nhanh chóng

Giải phương trình bậc 2 là đi tìm các giá trị của x sao cho khi thay x vào phương trình ( 1 ) thì thỏa mãn nhu cầu ax2 + bx + c = 0 .

Bước 1: Tính Δ=b2-4ac

Bước 2 : So sánh Δ với 0

• Nếu Δ>0: phương trình tồn tại 2 nghiệm: x1 = (-b + √Δ )/2a và x2 = (-b – √Δ )/2a
• Nếu Δ=0, phương trình có nghiệm kép x= – b/2a
• Nếu Δ<0, phương trình đã cho vô nghiệm.

Trong trường hợp b = 2 b ’, để đơn thuần ta hoàn toàn có thể tính Δ ’ = b ’ 2 – ac, tương tự như như trên :

• Nếu Δ’ < 0 thì phương trình bậc 2 vô nghiệm.
• Nếu Δ’ = 0 thì phương trình bậc 2 có nghiệm kép x1 = x2 = -b’/a.
• Nếu Δ’ > 0 thì phương trình bậc 2 có nghiệm x1 = (-b’ + √Δ’ )/a và x2 = (-b’ – √Δ’ )/a

2. Định lý Viet

Công thức Vi-ét về quan hệ giữa các nghiệm của đa thức với các thông số của nó. Trong trường hợp phương trình bậc hai một ẩn, được phát biểu như sau :
Gọi x1, x2 là nghiệm của phương trình bậc 2 một ẩn ax2 + bx + c ( a ≠ 0 ) thì :

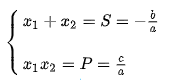
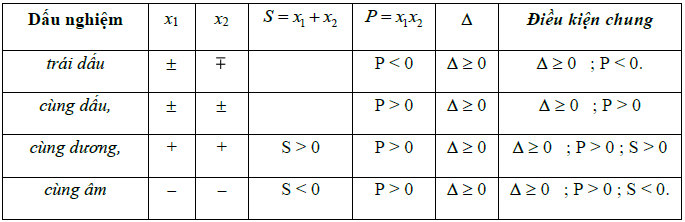
• Nếu S<0, x1 và x2 trái dấu.
• Nếu S>0, x1 và x2 cùng dấu:
• P>0, hai nghiệm cùng dương.
• P<0, hai nghiệm cùng âm.

3. Định lý Viet hòn đảo

Nếu x1 + x2 = S và x1. x2 = P thì x1, x2 là 2 nghiệm của phương trình x2 – Sx + P = 0 ( Điều kiện S2 – 4P > 0 )

4. Trường hợp đặc biệt

Nếu phương trình bậc hai có :

• a + b + c = 0 (với a, b, c là các hệ số của phương trình bậc 2, a≠0) thì nghiệm của phương trình là: x1 = 1; x2 = c/a
• a – b + c =0 (với a, b, c là các hệ số của phương trình bậc 2, a≠0) thì nghiệm của phương trình là: x1 = – 1; x2 = – c/a
• Nếu ac < 0 (a, c trái dấu nhau) thì phương trình luôn có 2 nghiệm phân biệt trái dấu.

Các dạng bài tập về phương trình bậc 2

1. Dạng 1: Phương trình bậc 2 một ẩn không xuất hiện tham số.

Để giải các phương trình bậc 2, cách thông dụng nhất là sử dụng công thức tính Δ hoặc Δ ’, rồi vận dụng các điều kiện kèm theo và công thức của nghiệm đã được nêu ở phần công thức nghiệp .
Ví dụ 1 : 2×2 – 7 x + 3 = 0 ( 3 )
Tính Δ = ( – 7 ) 2 – 4.2.3 = 49 – 24 = 25 > 0 => ( 3 ) có 2 nghiệm phân biệt :

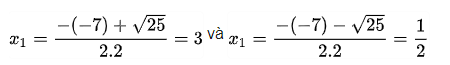
Ví dụ 2 : Phương trình 2×2 + 6 x + 5 = 0
Ta có : a = 2 ; b = 6 ; c = 5
Biệt thức Δ = b2 − 4 ac = 62 − 4.2.5 = 36 − 40 = − 4
Δ = – 4 < 0 => phương trình vô nghiệm .
Ví dụ 3 : Phương trình x2 − 4 x + 4 = 0
Ta có : a = 1 ; b = – 4 ; c = 4
Biệt thức Δ = b2 − 4 ac = ( − 4 ) 2 − 4.1.4 = 16 − 16 = 0
Vì Δ = 0 => phương trình có nghiệm kép x1 = x2 = − b / 2 a = − ( − 4 ) / 2.1 = 4/2 = 2

2. Dạng 2: Phương trình khuyết hạng tử

Khuyết hạng tử bậc nhất : ax2 + c = 0 ( 1 ) .

<=> x2 = – c/a

• Nếu -c/a>0, nghiệm là:
• 
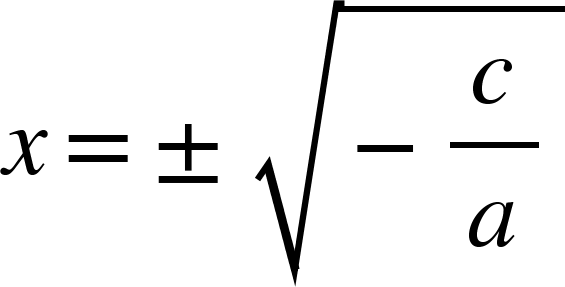
  Nếu -c/a=0, nghiệm x=0
• Nếu -c/a<0, phương trình vô nghiệm.

Khuyết hạng tử tự do : ax2 + bx = 0 ( 2 ). thì

Ví dụ : x2 + 9 = 0

<=> x2 = – 9

<=> x1 = 3 hoặc x2 = -3

3. Dạng 3: Nhẩm nghiệm phương trình bậc 2

Dạng 1: A = 1, B = Tổng, C = Tích

Nếu phương trình có dạng x2 – ( u + v ) x + uv = 0 thì phương trình đó có hai nhiệm u và v .
Nếu phương trình có dạng x2 + ( u + v ) x + uv = 0 thì phương trình có hai nghiệm – u và – v .
Tóm lại :
x2 – ( u + v ) x + uv = 0 => x1 = u, x2 = v ( 1 )
x2 + ( u + v ) x + uv = 0 => x1 = – u, x2 = – v
Ví dụ : 3×2 – 4 x + 1 = 0
Giải :
Nhận thấy vì a + b + c = 3 + ( – 4 ) + 1 = 0 => phương trình có nghiệm là : x1 = 1 và x2 = c / a = 1/3 .

Dạng 2: A + B + C = 0 và A – B + C = 0

x2 – ( u + v ) x + uv = 0 => x1 = u, x2 = v ( 1 )

• Nếu thay v = 1 vào (1) thì chúng ta sẽ có trường hợp nhẩm nghiệm quen thuộc a + b + c = 0, với a = 1, b = -(u+1), c= u.
• Nếu thay v = -1 vào (1) thì bạn sẽ có trường hợp nhẩm nghiệm a – b + c = 0, với a = 1, b = -(u-1), c = -u.

Dạng 3: Hai nghiệm là nghịch đảo của nhau

Nếu u ≠ 0 và v = 1 / u thì phương trình ( 1 ) có dạng :

Phương trình có hai nghiệm là nghịch đảo của nhau x = u, x = 1 / u. Đây cũng là trường hợp hay gặp khi giải toán .
Ví dụ phương trình :
2×2 – 5 x + 2 = 0 có hai nghiệm x = 2, x = 1/2
3×2 – 10 x + 3 = 0 có hai nghiệm x = 3, x = 1/3

4. Dạng 4: Xác định điều kiện tham số để nghiệm thỏa yêu cầu đề bài

Phương pháp : để nghiệm thỏa nhu yếu đề bài, thứ nhất phương trình bậc 2 phải có nghiệm. Vì vậy, ta triển khai theo các bước sau :

• Tính Δ, tìm điều kiện để Δ không âm.
• Dựa vào định lý Viet, ta có được các hệ thức giữa tích và tổng, từ đó biện luận theo yêu cầu đề.

Ví dụ : Cho phương trình 3×2 – 2 ( m + 1 ) x + 3 m – 5 = 0. Xác định m để phương trình có một nghiệm gấp 3 nghiệm kia. Tính các nghiệm trong trường hợp đó .
Giải :
Ta có : 3×2 – 2 ( m + 1 ) x + 3 m – 5 = 0 ( * )
Theo nhu yếu đề bài : để phương trình có một nghiệm gấp 3 nghiệm kia có nghĩa là phương trình có 2 nghiệm phân biệt thì Δ ’ > 0

<=> (m + 1)2 -3.(3m – 5) > 0

<=> m2 + 2m + 1 – 9m + 15 > 0

<=> m2 -7m + 16 > 0

<=> (m – 7/2)2 + 15/4 > 0

Ta thấy, Δ ’ > 0 với mọi m ∈ R nên phương trình ( * ) luôn có hai nghiệm phân biệt .
Gọi x1, x2 là hai nghiệm của phương trình, khi đó theo định lý Vi-ét ta có :

Theo đề bài phương trình có một nghiệm gấp 3 lần nghiệm kia, nên không tính tổng quát khi giả sử x2 = 3. x1 thay vào ( 1 )

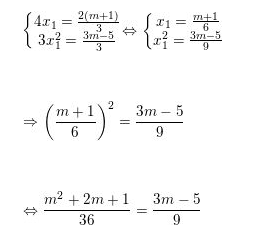
<=> m2 + 2m + 1 = 4(3m – 5)

<=> m2 -10m + 21 = 0

<=> m = 3 hoặc m = 7

+ TH1 : Với m = 3, phương trình ( * ) trở thành 3×2 – 8 x + 4 = 0 có hai nghiệm là x1 = 2/3 và x2 = 2 thỏa mãn nhu cầu điều kiện kèm theo .
+ TH2 : Với m = 7, phương trình ( * ) trở thành 3×2 – 16 x + 16 = 0 có hai nghiệm là x1 = 4/3 và x2 = 4 thỏa mãn nhu cầu điều kiện kèm theo .
Kết luận : m = 3 thì phương trình có 2 nghiệm là 2/3 và 2 ; m = 7 thì phương trình có 2 nghiệm là 4/3 và 4 .

5. Dạng 5: Phân tích thành nhân tử

Phương trình bậc 2 : ax2 + bx + c = 0 có 2 nghiệm phân biệt x1, x2, khi nào bạn cũng hoàn toàn có thể viết nó về dạng sau :
ax2 + bx + c = a ( x-x1 ) ( x-x2 ) = 0 .
Trở lại với phương trình ( 2 ), sau khi tìm ra 2 nghiệm x1, x2 bạn hoàn toàn có thể viết nó về dạng : 4 ( x-3 / 2 ) ( x + 1 ) = 0 .
Hy vọng với những thông tin mà chúng tôi vừa san sẻ hoàn toàn có thể giúp bạn giải phương trình bậc 2 với các dạng bài tập khác nhau đơn thuần. Chúc các bạn thành công xuất sắc !

Đánh giá bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp