Phương trình lượng giác cơ bản và cách giải – Toán Thầy Định

Để giải một phương trình lượng giác nói chung người ta tìm cách đưa nó về các phương trình lượng giác đơn thuần hơn. Trong đó có 4 dạng phương trình lượng giác có dạng đơn thuần nhất. Chúng được gọi là phương trình lượng giác cơ bản. Vậy chúng gồm những phương trình như thế nào. Cách giải chúng ra sao. Bài viết dưới đây sẽ hướng dẫn các bạn điều đó .

1. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN LÀ GÌ

Có 4 dạng phương trình lượng giác cơ bản là sinx=a; cosx=a; tanx=a; cotx=a. Trong đó x là ẩn và a là một số thực.

Có 2 cách để các bạn hoàn toàn có thể ghi nhớ công thức nghiệm của chúng. Một là học thuộc lòng công thức. Hai là sử dụng hình ảnh đường tròn lượng giác để nhớ .

Mỗi cách đều có ưu nhược điểm riêng, tùy các bạn lựa chọn. Còn tôi thì dùng cách thứ hai vì nó rất khó để quên và đi vào bản chất hơn. Sau đây tôi sẽ hướng dẫn các bạn cách liên tưởng đến đường tròn lượng giác để nhớ công thức nghiệm nhé.

2. CÔNG THỨC NGHIỆM CỦA PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

• Phương trình sinx=a:

Hãy tưởng tượng rằng đường tròn lượng giác là một trục số được cuốn quanh một đường tròn đơn vị chức năng. Chiều dương cuốn theo chiều ngược chiều kim đồng hồ đeo tay. Chiều âm thì ngược lại. Chú ý gốc của nó đặt ở điểm A ( 1 ; 0 ). Như vậy mỗi một điểm trên đường tròn lượng giác đại diện thay mặt cho một giá trị của biến x. Chiếu điểm trên đường tròn lượng giác đó lên trục tung ta sẽ có giá trị của sinx. Như vậy giao điểm của đường thẳng y = a và đường tròn lượng giác chính là nghiệm của phương trình sinx = a .

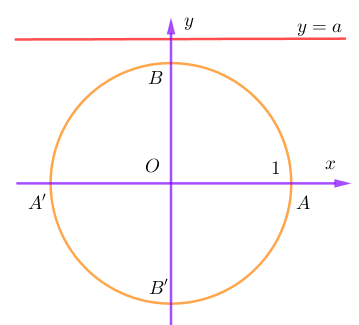
Rõ ràng, khi đã hiểu như vậy ta hoàn toàn có thể thấy ngay nếu a > 1 hoặc a < 1 thì đường thẳng y = a không cắt đường tròn lượng giác. Do đó trong các trường hợp này phương trình vô nghiệm .

Khi a=1 ta thấy đường y=a cắt đường tròn lượng giác tại điểm B (hình). Trên đường tròn lượng giác thì điểm B biểu diễn cho các giá trị

. Trong đó k là số nguyên bất kỳ.

Tương tự, khi a=-1 ta thấy đường y=a cắt đường tròn lượng giác tại điểm B’ (hình). Trên đường tròn lượng giác thì điểm B’ biểu diễn cho các giá trị

. Trong đó k là số nguyên bất kỳ.

Khi -1

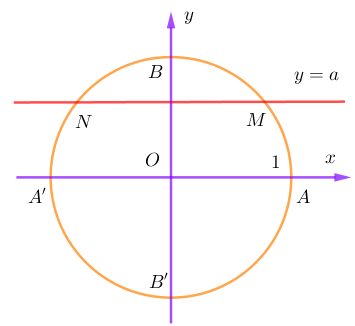
Ta lại thấy 2 điểm M, N đối xứng với nhau qua trục tung. Do đó nếu điểm M biểu diễn cho giá trị

thì N sẽ biểu diễn cho giá trị và ngược lại. Trong đó k, l là số nguyên. Nghĩa là trong trường hợp này ta chỉ cần xác định được giá trị α để sinα=a thì công thức của phương trình sinx=a được xác định như trên.
Tóm lại :

• Phương trình cosx=a:

Với phương trình cosx = a ta cũng lập luận trọn vẹn tựa như như trên. Chỉ khác số nghiệm của phương trình là số giao điểm của đường tròn lượng giác và đường thẳng x = a .
Nếu a > 1 hoặc a < 1 thì đường thẳng x = a không cắt đường tròn lượng giác. Do đó phương trình vô nghiệm .

Nếu a=1 thì đường thẳng x=a cắt đường tròn lượng giác tại điểm duy nhất A. Điểm A biểu diễn cho giá trị

. Trong đó k là số nguyên.

Nếu a=-1 thì đường thẳng x=a cắt đường tròn lượng giác tại điểm duy nhất A’. Điểm A’ biểu diễn cho giá trị . Trong đó k là số nguyên.

Nếu -1 thì điểm N biểu diễn cho giá trị . Trong đó k, l là các số nguyên.

Tóm lại :

• Phương trình tanx=a:

Như tất cả chúng ta đã biết, để xác lập giá trị của tanx. Ta xác lập giao điểm của OM và trục tang. Trong đó M là điểm màn biểu diễn cho x trên đường tròn lượng giác. Còn trục tang là trục có gốc tại A. Chiều dương cùng chiều trục tung .
Vì vậy để xác lập nghiệm của phương trình tanx = a ta xác lập giao điểm của đường thẳng OT với đường tròn lượng giác. Trong đó T là điểm màn biểu diễn cho giá trị của a trên trục tang .

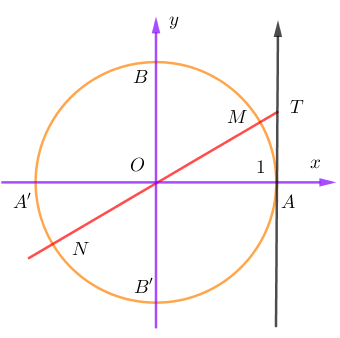
Ta thấy với mọi giá trị của a thì OT luôn cắt đường tròn lượng giác tại hai điểm. Chẳng hạn là M và N. Ta lại thấy M và M đối xứng với nhau qua tâm O. Do đó nếu M biểu diễn cho giá trị thì N sẽ biểu diễn cho giá trị . Trong đó k, l là các số nguyên. Tuy nhiên ta có thể viết gộp giá trị mà 2 điểm M, N biểu diễn lại là .

Tóm lại :

trong đó α là một giá trị nào đó mà tanα = a .

• Phương trình cotx=a:

Phương trình cotx = a được suy luận trọn vẹn giống phương trình tanx = a. Chỉ có điều trục cotang có gốc ở điểm B ( 0 ; 1 ) và có chiều dương cùng chiều với trục hoành. Từ đó ta thu được :

trong đó α là một giá trị nào đó mà cotα = a .

3. GIẢI MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

Dưới đây là một số ví dụ đơn giản để các bạn có thể hiểu rõ hơn.

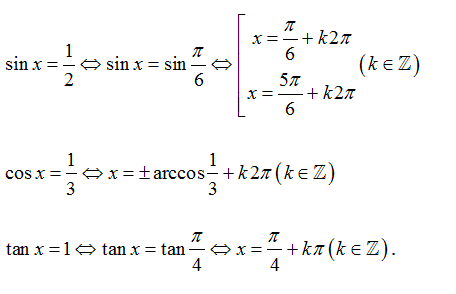
Chúc các bạn học tập vui tươi !
Lượng Giác –

Source: http://wp.ftn61.com
Category: Hỏi Đáp