Cách Tính Chu Vi Hình Tam Giác Lớp 3, Công Thức Tính Diện Tích, Chu Vi Hình Tam Giác

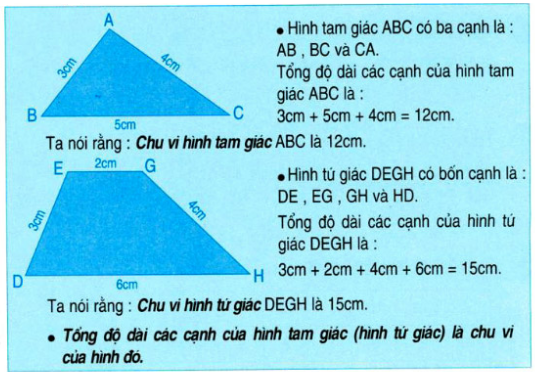
Tam giác hay còn gọi là hình tam giác, có 3 điểm, 3 cạnh và 3 góc với tổng số góc bằng 180 o. Hình tam giác được chia ra thành những loại : Tam giác thường, Tam giác cân, Tam giác đều, Tam giác tù, Tam giác vuông, Tam giác vuông cân và Tam giác nhọn .
Đang xem : Cách tính chu vi hình tam giác lớp 3

Công thức tính Diện tích, Chu vi hình Tam giác

Công thức Tính diện tích tam giác Công thức Tính chu vi tam giác 8 công thức tính diện tích tam giác nâng cao

Để tính được diện tích quy hoạnh, chu vi hình tam giác, bạn cần xác lập được đó là loại tam giác gì. Từ đó mới tìm ra công thức tính đúng chuẩn. Vậy mời những bạn cùng theo dõi bài viết dưới đây để hiểu rõ hơn :

Phân loại hình tam giác

Tam giác thường: Là loại tam giác cơ bản nhất, có độ dài các cạnh khác nhau, số đo góc trong cũng khác nhau.

Tam giác cân: Là tam giác có 2 cạnh, 2 góc bằng nhau. Đỉnh của tam giác cân là giao điểm của 2 cạnh bên.

Tam giác vuông cân: Vừa là tam giác vuông, vừa là tam giác cân. Có 2 cạnh góc vuông bằng nhau và mỗi góc nhọn bằng 45°.

Tam giác ABC có 3 cạnh a, b, c, ha là đường cao từ đỉnh A. Các công thức tính diện tích quy hoạnh tam giác thường :
Công thức chung :
Diện tích tam giác bằng ½ tích của chiều cao hạ từ đỉnh với độ dài cạnh đối lập của đỉnh đó :

Khi biết một góc :
Diện tích tam giác bằng ½ tích 2 cạnh và sin của góc hợp bởi 2 cạnh đó :

Sử dụng công thức Heron :

Trong đó p là nửa chu vi tam giác :

Vậy công thức sẽ là :

Với R là nửa đường kính đường tròn ngoại tiếp tam giác :

Cách khác :

Với r là nửa đường kính đường tròn nội tiếp tam giác :

Diện tích tam giác đều

Tam giác đều ABC có 3 cạnh bằng nhau, trong đó a là độ dài những cạnh của tam giác, nên thuận tiện vận dụng định lý Heron để suy ra :

Diện tích tam giác cân

Diện tích tam giác cân đối tích độ cao nối từ đỉnh tam giác đó tới cạnh đáy tam giác, rồi chia cho 2. Trong đó, a là độ dài cạnh đáy, chiều cao là ha :

Diện tích tam giác vuông

Tam giác vuông ABC, có độ dài 2 cạnh góc vuông lần lượt là a, b. Công thức tính diện tích quy hoạnh tam giác vuông là :

Diện tích tam giác vuông cân

Tam giác ABC, vuông cân tại A, a là độ dài 2 cạnh góc vuông :

Công thức Tính chu vi tam giác

Chu vi tam giác thường

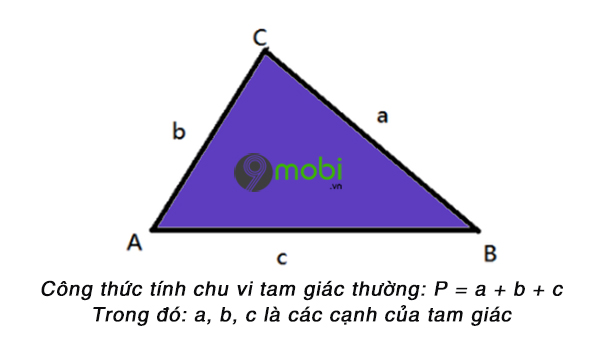
Công thức tính chu vi hình tam giác thường bằng độ dài tổng 3 cạnh của tam giác đó :

Trong đó :
P. là chu vi tam giác. a, b, c là 3 cạnh của hình tam giác đó .
Theo đó, nếu muốn tính diện tích quy hoạnh nửa chu vi tam giác sẽ dựa theo công thức :

Chu vi tam giác vuông

Công thức tính chu vi tam giác vuông :

Trong đó :
a và b : Hai cạnh của tam giác vuông c : Cạnh huyền của tam giác vuông .

Chu vi tam giác cân

Tam giác cân là tam giác có 2 cạnh bên bằng nhau, nên công thức tính chu vi tam giác cân sẽ như sau :

Trong đó :
a : Hai cạnh bên của tam giác cân. c : Là đáy của tam giác .

Lưu ý: Công thức tính chu vi tam giác cân cũng được áp dụng để tính chu vi của tam giác vuông cân.

Chu vi tam giác đều

Tam giác đều là tam giác có 3 cạnh bằng nhau, vậy công thức tính chu vi tam giác đều sẽ là :

Trong đó:

P. : Là chu vi tam giác đều. a : Là chiều dài cạnh của tam giác .

8 công thức tính diện tích tam giác nâng cao

Cho tam giác ABC, ta kí hiệu độ dài những cạnh là a = BC, b = CA, c = AB, những góc của tam giác được viết đơn thuần là A, B, C. Diện tích tam giác được kí hiệu là S .
Xem thêm : Dự Án Kinh Doanh Đồ Ăn Nhanh Và Nước Uống ( 2 ), Kế Hoạch Kinh Doanh Đồ Ăn Nhanh Và Đồ Uống

Công thức 1

Gọi độ dài đường cao ( độ cao ) hạ từ những đỉnh A, B, C lần lượt là ha, hb, hc .
Xem thêm : đồ án xây dựng map địa hình

Đặc biệt :
Diện tích tam giác vuông tại A là :
Diện tích tam giác cân tại A là :
( với H là trung điểm của BC ) .
Diện tích tam giác đều cạnh a là :

Công thức 2

Công thức 3

Gọi R là nửa đường kính đường tròn ngoại tiếp tam giác ABC. Ta có :

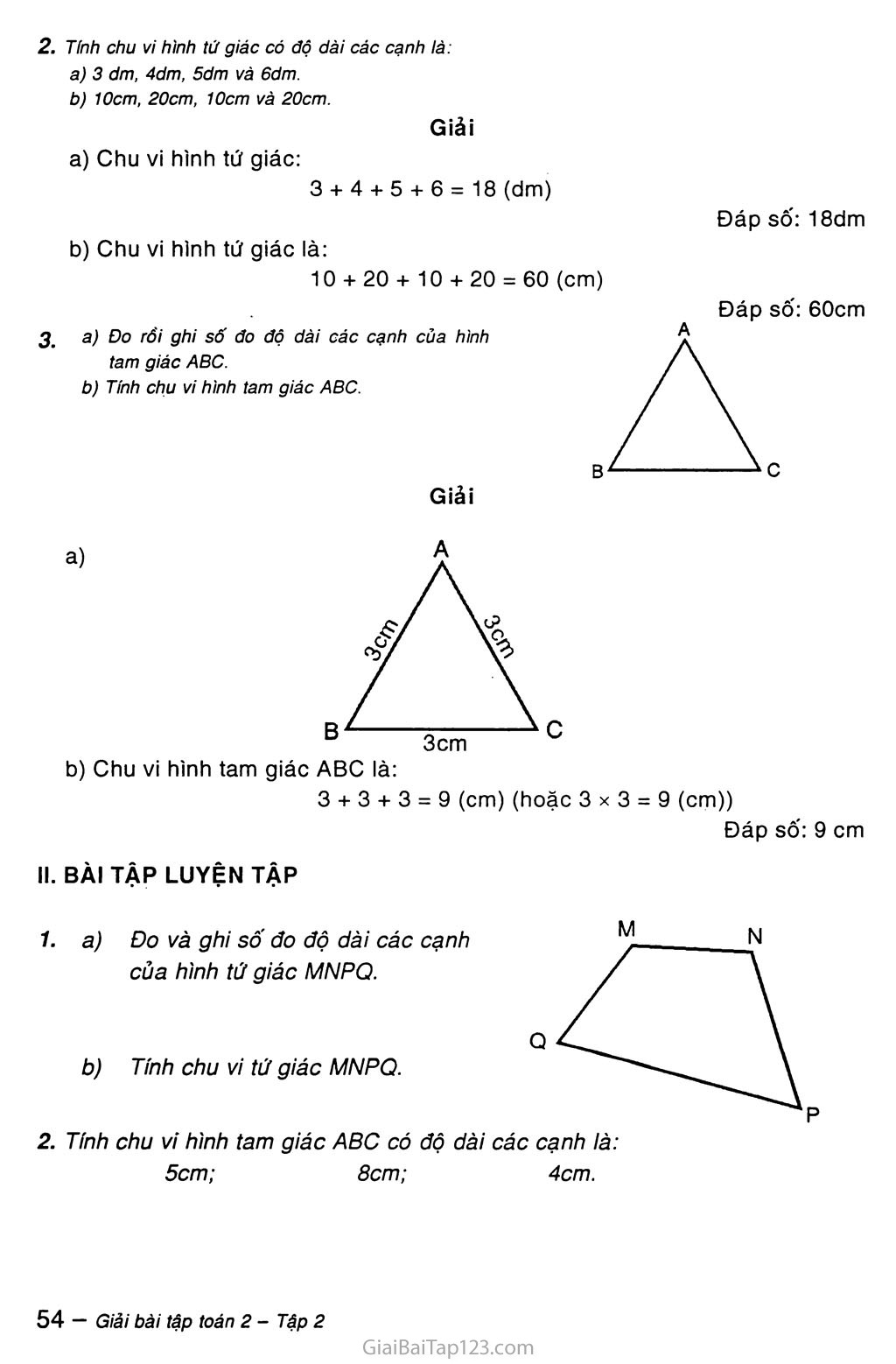
Công thức 4

Gọi r là nửa đường kính đường tròn nội tiếp tam giác ABC và p là nửa chu vi tam giác (
) :

Công thức 5 (Công thức Héron)

Với p là kí hiệu nửa chu vi như ở mục 4, ta có :

Công thức 6

Công thức 7

Trong mặt phẳng Oxy, gọi tọa độ các đỉnh của tam giác ABC là: A(xA,yA),B(xB,yB),C(xC,yC).Khi đó:

Công thức 8

Áp dụng trong khoảng trống, với khái niệm tích có hướng của 2 vectơ. Ta có :

Xem thêm bài viết thuộc chuyên mục: Cách tính

Điều hướng bài viết

Source: http://wp.ftn61.com
Category: Thủ Thuật