✅ Công thức Bernoulli ⭐️⭐️⭐️⭐️⭐

1/5 – ( 1 bầu chọn )

Tóm tắt lý thuyết

Trong nhiều bài toán thực tiễn, ta thường gặp trường hợp cùng một phép thử được lặp đi lặp lại nhiều lần. Trong mỗi phép thử hoàn toàn có thể xảy ra hay không xảy ra một biến cố A nào đó và ta chăm sóc đến tổng số lần xảy ra biến cố A trong dãy phép thử. Chẳng hạn, nếu thực thi sản xuất hàng loạt một loại chi tiết cụ thể nào đó ta thường chăm sóc đến tổng số cụ thể đạt tiêu chuẩn của cả quy trình sản xuất. Bài toán này hoàn toàn có thể xử lý khá thuận tiện nếu những phép thử độc lập với nhau .
Các phép thử được gọi là độc lập với nhau nếu Xác Suất để xảy ra một biến cố nào đó trong từng phép thử sẽ không nhờ vào vào việc biến cố đó có xảy ra ở phép thử khác hay không. Chẳng hạn : tung nhiều lần một đồng xu hoặc lấy ngẫu nhiên có hoàn trả n mẫu sản phẩm từ một lô hàng sẽ tạo nên những phép thử độc lập .
Giả sử thực thi n phép thử độc lập. Trong mỗi phép thử chỉ hoàn toàn có thể xảy ra một trong hai trường hợp : Hoặc biến cố A xảy ra hoặc biến cố A không xảy ra. Xác suất xảy ra biến cố A trong mỗi phép thử đều bằng p và Xác Suất A không xảy ra bằng 1 – p = q. Khi dó Tỷ Lệ để trong n phép thử độc lập nói trên biến cố A xảy ra đúng k lần ký hiệu là Pk ( A ) được tính theo công thức Bemoulli sau đây :

(k = 0, 1,2,…, n)

Chứng minh: Gọi Ai là biến cố “ở phép thử thứ i, A xảy ra” (i = 1, 2,…, n). Suy ra

sẽ là biến cố “ ở phép thử thứ i, A không xảy ra ”. Gọi B là biến cố “ trong n phép thử, A xảy ra đúng k lần ”. B hoàn toàn có thể xảy ra theo nhiều cách khác nhau. Chẳng hạn, k phép thử đầu, A xảy ra, còn n-k phép thử sau A không xảy ra. Trường hợp này ta hoàn toàn có thể màn biểu diễn bằng biến cố tích :

Hoặc n-k phép thử đầu A không xảy ra, còn n-k phép thử cuối A xảy ra. Trường hợp này ta hoàn toàn có thể màn biểu diễn bằng biến cố tích có dạng :

Tổng số những tích như vậy chính là số cách chọn k phép thử để biến cố A xảy ra, tức bằng

và biến cố B chính là tổng của những biến cố tích ấy .

Giả thuyết Bernoulli là gì? Phép thử Bernoulli và ứng dụng vào xác suất thống kê

Daniel Bernoulli, nhà toán học của thế kỷ 19, đã đưa ra lời giải cho một nghịch lý nổi tiếng với cái tên “nghịch lý Xanh Pê-téc-bua”, đó là giả thuyết Bernoulli.

Giả thuyết Bernoulli là gì?

Giả thuyết Béc-nu-li (Bernoulli hypothesis) Daniel Bernoulli là nhà toán học của thế kỷ 19, đã đưa ra lời giải cho một nghịch lý nổi tiếng với cái tên “nghịch lý Xanh Pê-téc-bua”.

Vấn đề là phải lý giải tại sao con người không trả những khoản tiền cực lớn để chơi game show sau đây : Một đồng xu tiền được tung lên, ví dụ điển hình cho đến khi mặt ngửa Open. nếu mặt ngửa Open ở lần tung thứ hai, người chơi nhận được 2 ² đơn vị chức năng tiền thưởng ( ví dụ là 4 đồng ). Nếu mặt ngửa Open ở lần tung thứ 3, người chơi nhận được 2 ³ đơn vị chức năng tiền thưởng, đến lần thứ tư người chơi nhận được 2 ∧ 4 đơn vị chức năng tiền thưởng, và vân vân. Tổng của Xác Suất nhận được tiền thưởng phải bằng 1, nhưng với số lần tung vô hạn, giá trị kỳ vọng của tiền thưởng cũng là một đại lượng vô hạn. Như vậy, người ta hoàn toàn có thể nhận định và đánh giá rằng người chơi sẽ đánh những khoản tiền rất lớn trong một game show như vậy .
Giải thích tại sao mọi người đồng ý chơi game show này, Bernoulli lập luận rằng người chơi bạc chăm sóc đến ích lợi của phần thưởng hơn là bản thân tiền thưởng. Bằng cách nêu ra giải thuyết về quyền lợi cận biên giảm dần của thu nhập, Bernoulli chỉ ra rằng một game show hoàn toàn có thể có giá trị kỳ vọng bằng tiền vô hạn, nhưng có giá trị kỳ vọng tính bằng lợi ích hữu hạn. Bởi vậy mọi người chăm sóc tới giả thuyết này trước hết vì nó là nỗ lực tiên phong trong việc thay thế sửa chữa tiềm năng tính bằng tiền bằng sự tối ưu hóa quyền lợi trong điều kiện kèm theo có rủi ro đáng tiếc hay tính bất định .

Phép thử Bernoulli và ứng dụng vào xác suất thống kê

Trước đó, vào thế kỳ 17, một nhà toán học nổi tiếng cũng thuộc nhà Bernoulli, Jacob Bernoulli đã phát minh ra phép thử Bernoulli. Dãy các phép thử Bernoulli được định nghĩa là đối với thí nghiệm ngẫu nhiên nào đó chúng ta thực hiện n lần
thử lặp lại. Chúng ta gọi dãy các phép thử này là dãy các phép thử Bernoulli nếu thoả mãn các điều kiện sau:

Đây là dãy các phép thử độc lập, nghĩa là kết quả của mỗi phép thử không
phụ thuộc vào kết quả của các phép thử khác.

Biến cố A xảy ra với xác suất p như nhau ở phép thử thứ i bất kỳ.

Nếu biến cố A xảy ra ở phép thử thứ i, ta nói phép thử thứ i thành công xuất sắc
Công thức của phép thử Bernoulli được viết như sau :

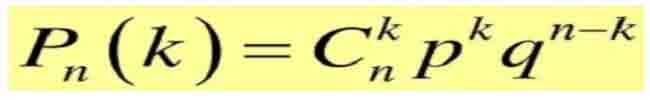
Công thức trên được dùng để tính Xác suất để biến cố A Open đúng k lần trong dãy n phép thử Bernoulli .

Source: http://wp.ftn61.com
Category: Thủ Thuật