Bạn đang đọc: BẢNG NGUYÊN HÀM và CÔNG THỨC NGUYÊN HÀM [SGK lớp 12]
5
/
5
(
1
bầu chọn
)
Trong chương trình toán trung học phổ thông thì bài toán nguyên hàm là một trong những dạng bài thường xuất hiện trong các đề thi đại học.
Tất cả các bài toán nguyên hàm và tích phân dù có phức tạp tới đâu thì sau khi biến đổi cũng sẽ trở về bảng công thức nguyên hàm đầy đủ.
Vì thế, chúng tôi sẽ tổng hợp các kiến thức lý thuyết và bảng công thức nguyên hàm từ cơ bản tới nâng cao đầy đủ nhất giúp các em làm bài tập tốt hơn và tiết kiệm thời gian hơn.
Tóm tắt nội dung bài viết
- I. Định nghĩa nguyên hàm là gì ?
- 1. Định lý của nguyên hàm
- 2. Các đặc thù của nguyên hàm
- II. Bảng công thức nguyên hàm cơ bản – từng phần – lượng giác – nâng cao
- 1. Công thức bảng nguyên hàm cơ bản
- 2. Công thức nguyên hàm từng phần
- 3. Công thức nguyên hàm lượng giác
- 4. Các công thức nguyên hàm nâng cao
- III. Dạng bài tập nguyên hàm thường gặp
- – Dạng 1 : Tìm nguyên hàm của hàm số
- – Dạng 2 : Tìm nguyên hàm của hàm số bằng chiêu thức đổi biến số
- – Dạng 3 : Tìm nguyên hàm bằng giải pháp từng phần
I. Định nghĩa nguyên hàm là gì ?
Định nghĩa: Cho hàm số f xác định trên tập K và hàm số F sẽ được gọi là nguyên hàm của hàm số f trên tập K khi F’(x) = f(x) và F(x) khả vi trên K với mọi x thuộc tập K.
Trong bộ môn giải tích thì nguyên hàm của hàm số thực cho trước f là 1 hàm F có đạo hàm bằng f, tức là F’ = f. Quá trình tìm nguyên hàm được gọi là tích phân bất định, việc tìm 1 biểu thức cho nguyên hàm là công việc khó khăn hơn so với việc tìm đạo hàm và không phải luôn luôn thực hiện được.
Xem thêm: Làm Thế Nào Để Jailbreak Iphone?
Tham khảo :
1. Định lý của nguyên hàm
- Nếu F ( x ) là 1 nguyên hàm của hàm số f ( x ) trên tập K thì mọi nguyên hàm của hàm số trên F ( x ) nằm trên tập K sẽ đều có dạng F ( x ) + C với C là hằng số .
- Nếu F ( x ) là 1 nguyên hàm của hàm số f ( x ) trên tập K thì với mỗi hằng số C, hàm số G ( x ) = F ( x ) + C cũng là nguyên hàm của f ( x ) trên tập K .
2. Các đặc thù của nguyên hàm
Nếu g ( x ) và f ( x ) là 2 hàm số liên tục trên tập K thì :

>>>Tham khảo thêm:
II. Bảng công thức nguyên hàm cơ bản – từng phần – lượng giác – nâng cao
Bảng công thức tính nguyên hàm là vô cùng quan trọng so với những bạn học viên lớp 12, đặc biệt quan trọng là phần học giải tích .
Dưới đây là tập hợp hàng loạt những công thức tính nguyên hàm cơ bản nhất kỳ vọng sẽ giúp những bạn mạng lưới hệ thống kiến thức và kỹ năng và vận dụng vào làm bài tập tốt hơn .
1. Công thức bảng nguyên hàm cơ bản

Bảng nguyên hàm cụ thể những công thức sau đây sẽ tương hỗ bạn giải toán nhanh hơn. Những công thức này không có quy luật để nhớ, cách duy nhất để bạn hoàn toàn có thể nhớ nhanh nhất chính là làm nhiều và sử dụng nhiều .
Bảng nguyên hàm khá đầy đủ có 10 công thức, những công thức này không phải quá phức tạp nên những bạn học viên đừng quá lo ngại mà chỉ cần làm nhiều bài tập thôi nhé .
2. Công thức nguyên hàm từng phần
Phương pháp nguyên hàm từng phần thường được sử dụng để tìm tích phân bất định của những hàm số phức tạp như vừa chứa hàm vô tỉ và hàm lượng giác, hoặc chứa hàm logarit và hàm vô tỉ, hay hàm mũ, …
Cho 2 hàm số u = u ( x ) và v = v ( x ) có đạo hàm trên tập K. Khi đó ta có công thức tính nguyên hàm từng phần như sau :
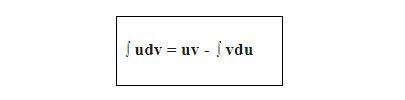
3. Công thức nguyên hàm lượng giác
Dưới đây là công thức nguyên hàm lượng giác nâng cao vận dụng để giải những bài toán khó .
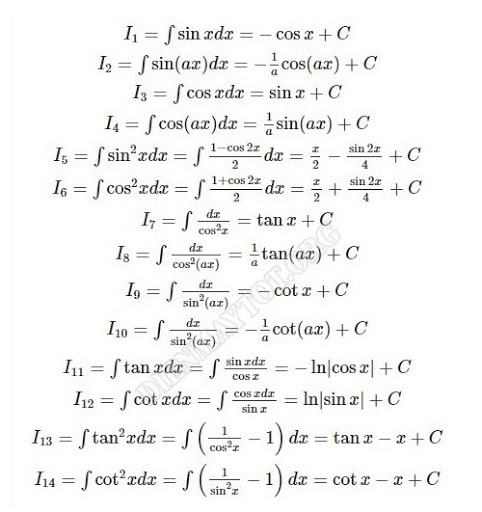
4. Các công thức nguyên hàm nâng cao
Bảng nguyên hàm nâng cao trong chương trình học đại trà phổ thông. Các công thức này để ship hàng những câu lấy điểm cao

III. Dạng bài tập nguyên hàm thường gặp
– Dạng 1 : Tìm nguyên hàm của hàm số
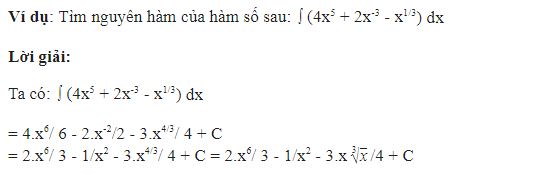
– Dạng 2 : Tìm nguyên hàm của hàm số bằng chiêu thức đổi biến số
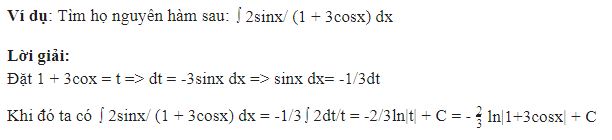
Xem thêm: Làm Thế Nào Để Iphone 6 Chạy Nhanh Hơn
– Dạng 3 : Tìm nguyên hàm bằng giải pháp từng phần

Việc ghi nhớ và sử dụng thành thạo bảng nguyên hàm hay bảng công thức nguyên hàm là điều bắt buộc. Các bạn hãy liệt kê ra những công thức hay dùng để có thể dễ dàng xem lại khi cần.
Điều này sẽ vô cùng hiệu quả nếu các em bắt đầu học 1 phần mới. Việc phân biệt nguyên hàm và vi phân cũng cần lưu ý, và các bạn cũng đừng nhầm lẫn giữa các nguyên hàm lượng giác. Nếu bạn vẫn chưa hiểu rõ phần nào, hãy để lại bình luận dưới bài viết này để cùng trao đổi và thảo luận nhé!
Source: http://wp.ftn61.com
Category: Thủ Thuật

Để lại một bình luận