Định nghĩa, phân loại và các đặc trưng của sóng cơ. Phương trình sóng cơ phụ thuộc vào thời gian và không gian được trình bày rất chi tiết.
SÓNG CƠ VÀ SỰ TRUYỀN SÓNG CƠ
A.LÝ THUYẾT
Bạn đang đọc: Lý thuyết sóng cơ và sự truyền sóng cơ
1.Sóng cơ- Định nghĩa- phân loại
+ Sóng cơ là những dao động lan truyền trong môi trường .
+ Khi sóng cơ truyền đi chỉ có pha xê dịch của những thành phần vật chất Viral còn những thành phần vật chất thì xê dịch xung quanh vị trí cân đối cố định và thắt chặt .
+ Sóng ngang là sóng trong đó các phần tử của môi trường dao động theo phương vuông góc với phương truyền sóng. Ví dụ: sóng trên mặt nước, sóng trên sợi dây cao su.
+ Sóng dọc là sóng trong đó các phần tử của môi trường dao động theo phương trùng với phương truyền sóng.
Ví dụ : sóng âm, sóng trên một lò xo .
2.Các đặc trưng của một sóng hình sin
+ Biên độ của sóng A: là biên độ dao động của một phần tử của môi trường có sóng truyền qua.
+ Chu kỳ sóng T: là chu kỳ dao động của một phần tử của môi trường sóng truyền qua.
+ Tần số f: là đại lượng nghịch đảo của chu kỳ sóng : f = \(\frac{1}{T}\)
+ Tốc độ truyền sóng v : là tốc độ lan truyền dao động trong môi trường. phụ thuộc bản chất môi trường (\(v_{R}> v_{L}> v_{K}\)) và nhiệt độ (nhiệt độ của môi trường tăng thì tốc độ lan truyền càng nhanh)
+ Bước sóng λ: là quảng đường mà sóng truyền được trong một chu kỳ. λ = vT = \(\frac{v}{f}\).
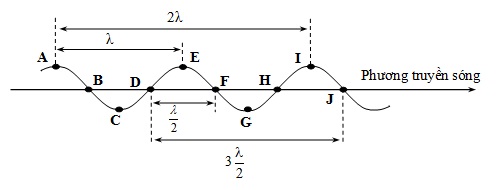
+Bước sóng λ cũng là khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng dao động cùng pha.
+ Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng mà xê dịch ngược pha là \ ( \ frac { \ lambda } { 2 } \ ) .+ Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng mà giao động vuông pha là \ ( \ frac { \ lambda } { 4 } \ ) .+ Khoảng cách giữa hai điểm bất kể trên phương truyền sóng mà xê dịch cùng pha là : kλ .
+ Khoảng cách giữa hai điểm bất kể trên phương truyền sóng mà giao động ngược pha là : ( 2 k + 1 ) \ ( \ frac { \ lambda } { 2 } \ ) .+ Lưu ý : Giữa n đỉnh ( ngọn ) sóng có ( n – 1 ) bước sóng .
3. Phương trình sóng:
a.Tại nguồn O: uO =Aocos(ωt)
b.Tại M trên phương truyền sóng:
uM=AMcosω(t- ∆t)
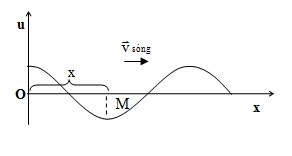
Nếu bỏ qua mất mát năng lượng trong quá trình truyền sóng thì biên độ sóng tại O và M bằng nhau: Ao = AM = A.
Thì: uM =Acosω(t – \(\frac{x}{v}\)) =Acos 2π(\(\frac{t}{T}-\frac{x}{\lambda }\)) Với t ≥ x/v
c.Tổng quát: Tại điểm O: uO = Acos(ωt + φ).
d.Tại điểm M cách O một đoạn x trên phương truyền sóng.
* Sóng truyền theo chiều dương của trục Ox thì :uM = AMcos ( ωt + φ – \ ( \ omega \ frac { x } { v } \ ) ) = AMcos ( ωt + φ – \ ( 2 \ pi \ frac { x } { \ lambda } \ ) ) t ≥ x / v* Sóng truyền theo chiều âm của trục Ox thì :
uM = AMcos(ωt + φ + \(\omega \frac{x}{v}\)) = AMcos(ωt +φ+ \(2\pi \frac{x}{\lambda }\))
–Tại một điểm M xác định trong môi trường sóng: x =const; uM là hàm điều hòa theo t với chu kỳ T.
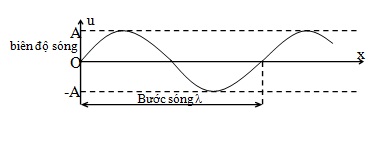
–Tại một thời điểm xác định t= const ; uM là hàm biến thiên điều hòa theo không gian x với chu kỳ λ.
e. Độ lệch pha giữa hai điểm cách nguồn một khoảng xM, xN: \(\Delta \varphi _{MN}=\omega \frac{x_{N}-x_{M}}{v}=2\pi \frac{x_{N}-x_{M}}{\lambda }\)
+ Nếu 2 điểm M và N giao động cùng pha thì :\ ( \ Delta \ varphi _ { MN } = 2 k \ pi \ Leftrightarrow 2 \ pi \ frac { x_ { N } – x_ { M } } { \ lambda } = 2 k \ pi \ Leftrightarrow x_ { N } – x_ { M } = k \ lambda ( k \ in Z ) \ )+ Nếu 2 điểm M và N giao động ngược pha thì :\ ( \ Delta \ varphi _ { MN } = ( 2 k + 1 ) \ pi \ Leftrightarrow 2 \ pi \ frac { x_ { N } – x_ { M } } { \ lambda } = ( 2 k + 1 ) \ pi \ ) \ ( \ Leftrightarrow x_ { N } – x_ { M } = ( 2 k + 1 ) \ frac { \ lambda } { 2 } ( k \ in Z ) \ )+ Nếu 2 điểm M và N giao động vuông pha thì :\ ( \ Delta \ varphi _ { MN } = ( 2 k + 1 ) \ frac { \ pi } { 2 } \ Leftrightarrow 2 \ pi \ frac { x_ { N } – x_ { M } } { \ lambda } = ( 2 k + 1 ) \ frac { \ pi } { 2 } \ ) \ ( \ Leftrightarrow x_ { N } – x_ { M } = ( 2 k + 1 ) \ frac { \ lambda } { 4 } ( k \ in Z ) \ )- Nếu 2 điểm M và N nằm trên một phương truyền sóng và cách nhau một khoảng chừng x thì :\ ( \ Delta \ varphi = \ omega \ frac { x } { v } = 2 \ pi \ frac { x } { \ lambda } \ )
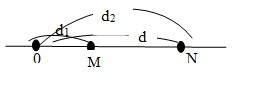
(Nếu 2 điểm M và N trên phương truyền sóng và cách nhau một khoảng d thì : \(\Delta \varphi =\frac{2\pi d}{\lambda }\) )
– Vậy 2 điểm M và N trên phương truyền sóng sẽ :
+ dao động cùng pha khi: d = kλ
+ dao động ngược pha khi: d = (2k + 1)\(\frac{\lambda }{2}\)
Xem thêm: Làm Thế Nào Để Update Win 7 Lên Win 10?
+ dao động vuông pha khi: d = (2k + 1)\(\frac{\lambda }{4}\)
với k = 0, ±1, ±2 …
Lưu ý: Đơn vị của x, x1, x2,d, l và v phải tương ứng với nhau.
f. Trong hiện tượng truyền sóng trên sợi dây, dây được kích thích dao động bởi nam châm điện với tần số dòng điện là f thì tần số dao động của dây là 2f.
B. VÍ DỤ
Ví dụ 1: Một người ngồi ở bờ biển trông thấy có 10 ngọn sóng qua mặt trong 36 giây, khoảng cách giữa hai ngọn sóng là 10m.. Tính tần số sóng biển.và vận tốc truyền sóng biển.
A. 0,25 Hz ; 2,5 m / s B. 4H z ; 25 m / s C. 25H z ; 2,5 m / s D. 4H z ; 25 cm / s
Hướng dẫn giải: Xét tại một điểm có 10 ngọn sóng truyền qua ứng với 9 chu kì. T= \(\frac{36}{9}\) = 4s. Xác định tần số dao động. \(f=\frac{1}{T}=\frac{1}{4}=0,25Hz\) .Vận tốc truyền sóng:\(\lambda =vT\Rightarrow v=\frac{\lambda }{T}=\frac{10}{4}=2,5(m/s)\) .
Đáp án A
Ví dụ 2: Một sóng cơ truyền trên một sợi dây đàn hồi rất dài. Phương trình sóng tại một điểm trên dây: u = 4cos(20π t – \(\frac{\pi x}{3}\) )(mm).Với x: đo bằng met, t: đo bằng giây. Tốc độ truyền sóng trên sợi dây có giá trị.
A. 60 mm / s B. 60 cm / s C. 60 m / s D. 30 mm / s
Hướng dẫn giải: Ta có= \(\frac{\pi x}{3}\) \(=\frac{2\pi x}{\lambda }\) => λ = 6 m => v = λ.f = 60 m/s (chú ý: x đo bằng met).
Đáp án C
Ví dụ 3: Một sóng cơ học truyền theo phương Ox với biên độ coi như không đổi. Tại O, dao động có dạng u = acosωt (cm). Tại thời điểm M cách xa tâm dao động O là \(\frac{1}{3}\) bước sóng ở thời điểm bằng 0,5 chu kì thì ly độ sóng có giá trị là 5 cm?. Phương trình dao động ở M thỏa mãn hệ thức nào sau đây:
A. \(u_{M}=acos(\omega t-\frac{2\lambda }{3})cm\) B. \(u_{M}=acos(\omega t-\frac{\pi \lambda }{3})cm\)
C. \(u_{M}=acos(\omega t-\frac{2\pi }{3})cm\) D. \(u_{M}=acos(\omega t-\frac{\pi }{3})cm\)
Chọn C
Hướng dẫn giải : Sóng truyền từ O đến M mất một thời gian là :t = \(\frac{d}{v}=\frac{\lambda }{3v}\)
Phương trình dao động ở M có dạng:\(u_{M}=acos\omega (t-\frac{1.\lambda }{v.3})\) .Với v =λ/T .Suy ra :
Ta có: \(\frac{\omega }{v}=\frac{2\pi }{T.\frac{\lambda }{T}}=\frac{2\pi }{\lambda }\) Vậy \(u_{M}=acos(\omega t-\frac{2\pi .\lambda }{\lambda .3})\) Hay : \(u_{M}=acos(\omega t-\frac{2\pi }{3})cm\)
C. BÀI TẬP TỰ LUYỆN
Bài 1 : Một người quan sát một chiếc phao trên mặt biển thấy phao nhấp nhô lên xuống tại chỗ 16 lần trong 30 giây và khoảng cách giữa 5 đỉnh sóng liên tiếp nhau bằng 24m. Tốc độ truyền sóng trên mặt biển là
A. v = 4,5m/s B. v = 12m/s. C. v = 3m/s D. v = 2,25 m/s
Bài 2: Một sóng cơ truyền dọc theo trục Ox có phương trình là \(u=5cos(6\pi t-\pi x)\) (cm), với t đo bằng s, x đo bằng m. Tốc độ truyền sóng này là
A. 3 m/s. B. 60 m/s. C. 6 m/s. D. 30 m/s.
Bài 3: Một sợi dây đàn hồi nằm ngang có điểm đầu O dao động theo phương đứng với biên độ A=5cm, T=0,5s. Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại M cách O d=50 cm.
A. \(u_{M}=5cos(4\pi t-5\pi )(cm)\) B. \(u_{M}=5cos(4\pi t-2,5\pi )(cm)\)
C. \(u_{M}=5cos(4\pi t-\pi )(cm)\) D. \(u_{M}=5cos(4\pi t- 25\pi )(cm)\)
Bài 4: Trên một sợi dây dài vô hạn có một sóng cơ lan truyền theo phương Ox với phương trình sóng u = 2cos(10πt – πx) (cm) ( trong đó t tính bằng s; x tính bằng m). M, N là hai điểm nằm cùng phía so với O cách nhau 5 m. Tại cùng một thời điểm khi phần tử M đi qua vị trí cân bằng theo chiều dương thì phần tử N
A. đi qua vị trí cân bằng theo chiều dương. B. đi qua vị trí cân bằng theo chiều âm.
C. ở vị trí biên dương. D. ở vị trí biên âm.
Bài 5: Cho phương trình sóng: \(u=asin(0,4\pi x+7\pi t+\frac{\pi }{3})\) (m, s). Phương trình này biểu diễn:
A. Sóng chạy theo chiều âm của trục x với vận tốc (m/s)
B. Sóng chạy theo chiều dương của trục x với vận tốc (m/s)
C. Sóng chạy theo chiều dương của trục x với vận tốc 17,5 (m/s)
D. Sóng chạy theo chiều âm của trục x với vận tốc 17,5 (m/s)
Bài 6: Một sóng ngang truyền trên sợi dây đàn hồi rất dài với tần số 500Hz. Người ta thấy hai điểm A,B trên sợi dây cách nhau 200cm dao động cùng pha và trên đoạn dây AB có hai điểm khác dao động ngược pha với A. Tốc độ truyền sóng trên dây lả:
A. 500cm/s B. 1000m/s C. 500m/s D. 250cm/s
Bài 7: Một dao động lan truyền trong môi trường liên tục từ điểm M đến điểm N cách M một đoạn 7λ/3(cm). Sóng truyền với biên độ A không đổi. Biết phương trình sóng tại M có dạng uM = 3cos2πt (uM tính bằng cm, t tính bằng giây). Vào thời điểm t1 tốc độ dao động của phần tử M là 6π(cm/s) thì tốc độ dao động của phần tử N là
A. 3π (cm/s). B. 0,5π (cm/s). C. 4π(cm/s). D. 6π(cm/s).
Bài 8: Một sóng cơ lan truyền trên sợi dây với chu kì T, biên độ A. Ở thời điểm t0, ly độ các phần tử tại B và C tương ứng là -24 mm và +24 mm; các phần tử tại trung điểm D của BC đang ở vị trí cân bằng. Ở thời điểm t1, li độ các phần tử tại B và C cùng là +10mm thì phần tử ở D cách vị trí cân bằng của nó
A.26mm B.28mm C.34mm D.17mm
Bài 9: Sóng lan truyền từ nguồn O dọc theo 1 đường thẳng với biên độ không đổi. Ở thời điểm t = 0, điểm O đi qua vị trí cân bằng theo chiều (+). Ở thời điểm bằng 1/2 chu kì một điểm cách nguồn 1 khoảng bằng 1/4 bước sóng có li độ 5cm. Biên độ của sóng là
A. 10cm B. 5\(\sqrt{3}\)cm C. 5\(\sqrt{2}\) cm D. 5cm
Bài 10: Một sóng cơ học lan truyền dọc theo 1 đường thẳng có phương truyền sóng tại nguồn O là :
uo = Acos ( \ ( \ frac { 2 \ pi } { T } t + \ frac { \ pi } { 2 } \ ) ) ( cm ). Ở thời gian t = 50% chu kì một điểm M cách nguồn bằng 1/3 bước sóng có độ di dời uM = 2 ( cm ). Biên độ sóng A là
A. 4cm. B. 2 cm. C. 4/\(\sqrt{3}\) cm. D. 2\(\sqrt{3}\) cm
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay
Source: http://wp.ftn61.com
Category: Thủ Thuật



Để lại một bình luận