Bảng 8 công thức tích phân cơ bản cần nhớ

tích phân, muốn học tốt phần này bạn cần nhớ bảng công thức tích phân cơ bản, biết cách vận dụng những công thức này sao cho hiệu quả. Bài viết này sẽ giúp bạn.Một chủ đề quan trọng thường Open trong đề thi là, muốn học tốt phần này bạn cần nhớ bảngcơ bản, biết cách vận dụng những công thức này sao cho hiệu suất cao. Bài viết này sẽ giúp bạn .

Để học hiệu quả bài này, bạn nên học theo trình tự từ kim chỉ nan, những công thức tích phân cơ bản, những dạng bài tích phân thường gặp. Sau khi học kĩ triết lý bạn nên những bài tập minh họa ở phần cuối .

1. Tích phân là gì?

Tích phân là kiến thức và kỹ năng quan trọng trong giải tích lớp 12. Ứng dụng quan trọng của tích phân dùng để tính diện tích quy hoạnh và thể tích của vật thể ..

2. Bảng công thức tích phân cơ bản

Ngoài khái niệm, muốn giải tốt tích phân bạn cần nhớ chính xác những công thức tích phân cơ bản dưới đây:

3. Phương pháp giải tích phân

3.1 Tính tích phân sử dụng bảng nguyên hàm cơ bản

3.2 Tích phân có chứa dấu giá trị tuyệt đối

3.3 Phương pháp đổi biến số trong tích phân

Một trong những chiêu thức thường dùng trong giải bài toán tích phân là đổi biến số, nghĩa là trải qua những đổi biến ta đưa một tích phân từ phức tạp về tích phân cơ bản. Từ đây ta dựa vào bảng tích phân để suy ra tác dụng .

3.4 Cách tính tích phân từng phần

Một giải pháp khá hay được nhiều thầy cô dạy đó là giải pháp tính tích phân từng phần, đây là giải pháp quan trọng giải được nhiều bài tập khó trong đề thi THPT Quốc gia. Phương pháp này có 1 công thức tổng quát và 4 dạng toán thường gặp .
Công thức tích phân từng phần tổng quát :

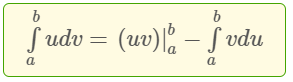
Lưu ý : Chúng ta thường hay gặp 4 dạng tích phân từng phần

• Dạng 1: Tích phân hàm số mũ

• Dạng 2: Tích phân hàm số logarit

• Dạng 3: Tích phân lượng giác

• Dạng 4: Tích phân hàm phức hợp giữa đa thức và lượng giác

4. Bài tập

Bài tập 1. (Câu 18 trích đề thi minh họa lần 2 năm 2019 – 2020)

Bài tập 2. (Vận dụng phương pháp đổi biến số giải câu 33 trích đề thi minh họa lần 2 năm 2019 – 2020)

Bài tập 3. (Giải câu 45 trích đề thi minh họa lần 2 năm 2019 – 2020)

Bài tập 4. Cho số thực a thỏa mãn $\int\limits_{ – 1}^a {{e^{x + 1}}dx} = {e^2} – 1$, khi đó a có giá trị bằng

A. 1 .
B. – 1 .

C. 0.

D. 2 .
Hướng dẫn giải
Ta có USD \ int \ limits_ { – 1 } ^ a { { e ^ { x + 1 } } dx } = \ left. { { e ^ { x + 1 } } } \ right | _ { – 1 } ^ a = { e ^ { a + 1 } } – e USD .
Vậy nhu yếu bài toán tương tự USD { e ^ { a + 1 } } – 1 = { e ^ 2 } – 1 { \ text { } } \ Leftrightarrow { \ text { } } a = 1 USD .

Bài tập 5. Nếu $\int\limits_{ – 2}^0 {\left( {4 – {e^{ – x/2}}} \right)dx} = K – 2e$ thì giá trị của K là

A. 12,5 .
B. 9 .
C. 11 .
D. 10 .
Hướng dẫn giải
USD \ begin { array } { * { 20 } { l } } \ begin { array } { l } K = \ int \ limits_ { – 2 } ^ 0 { \ left ( { 4 – { e ^ { – x / 2 } } } \ right ) dx } + 2 e \ \ = \ left. { \ left ( { 4 x + 2 { e ^ { – x / 2 } } } \ right ) } \ right | _ { – 2 } ^ 0 + 2 e \ end { array } \ \ { = 2 – \ left ( { – 8 + 2 e } \ right ) + 2 e = 10 } \ end { array } USD

Bài tập 6. Tích phân $I = \int\limits_{ – 2}^0 {x{e^{ – x}}dx} $ có giá trị bằng

A. USD – { e ^ 2 } + 1 USD .
B. USD 3 { e ^ 2 } – 1 USD .
C. USD – { e ^ 2 } – 1 USD .
D. USD – 2 { e ^ 2 } + 1 USD .
Hướng dẫn giải
Sử dụng tích phân từng phần, ta được
USD \ begin { array } { l } I = \ int \ limits_ { – 2 } ^ 0 { x { e ^ { – x } } dx } \ \ = – \ int \ limits_ { – 2 } ^ 0 { xd \ left ( { { e ^ { – x } } } \ right ) } \ \ = – \ left [ { \ left. { \ left ( { x { e ^ { – x } } } \ right ) } \ right | _ { – 2 } ^ 0 – \ int \ limits_ { – 2 } ^ 0 { { e ^ { – x } } dx } } \ right ] \ \ = – \ left. { \ left ( { x { e ^ { – x } } } \ right ) } \ right | _ { – 2 } ^ 0 + \ int \ limits_ { – 2 } ^ 0 { { e ^ { – x } } dx } \ \ = – \ left. { \ left ( { x { e ^ { – x } } } \ right ) } \ right | _ { – 2 } ^ 0 – \ left. { \ left ( { { e ^ { – x } } } \ right ) } \ right | _ { – 2 } ^ 0 \ \ = – { e ^ 2 } – 1. \ end { array } USD

Bài tập 7. Cho hàm số f liên tục trên đoạn [ 0;, 3]. Nếu $\int\limits_0^3 {f(x)dx} = 2$ thì tích phân $\int\limits_0^3 {\left[ {x – 2f(x)} \right]dx} $ có giá trị bằng

A. 7 .
B. 2,5 .
C. 5 .
D. 0,5 .

Hướng dẫn giải

USD \ begin { array } { l } \ int \ limits_0 ^ 3 { \ left [ { x – 2 f ( x ) } \ right ] dx } \ \ = \ int \ limits_0 ^ 3 { xdx } – 2 \ int \ limits_0 ^ 3 { f ( x ) dx } \ \ = \ frac { 9 } { 2 } – 2 \ times 2 = \ frac { 1 } { 2 } \ end { array } USD
Hy vọng với bài viết về công thức tích phân, giải pháp đổi biến số, cách tính tích phân từng phần ở trên có ích với bạn. Thấy hay hãy san sẻ tới mọi người và nhớ quay lại toanhoc.org để xem những chủ đề tiếp theo nhé .

Source: http://wp.ftn61.com
Category: Thủ Thuật