Công thức tính diện tích tam giác (vuông, thường, cân, đều)

Diện tích tam giác phải được chứng minh bằng nhiều công thức thường dùng cũng như khi sử dụng các công thức. Trong bài viết này, chúng tôi sẽ hướng dẫn các bạn những cách tính diện tích hình tam giác đơn giản và thông dụng nhất để có thể áp dụng ngay vào các bài kiểm tra.

Hình tam giác là gì ?

Hình tam giác là một hình phẳng 2 chiều có 3 điểm không thẳng hàng và 3 cạnh là ba đoạn thẳng nối những đỉnh. Hình tam giác là hình đa giác có ít cạnh nhất ( 3 cạnh ), tam giác luôn là một đa giác đơn thuần và luôn luôn là một đa giác lồi ( những góc trong luôn nhỏ hơn 180 º ) .

Các dạng hình tam giác trong toán học

Để có công thức Heron tính DT tam giác bạn cần xác định đó là loại tam giác gì, rồi sau đó sẽ tìm công thức tính DT một cách chính xác và những yếu tố cần để áp dụng công thức cách tính nhanh.

• Tam giác vuông: Đây là hình tam giác có góc 90 ^{\circ} (tức là góc vuông).
• Tam giác tù: Góc trong là tam giác có góc lớn hơn 90^{\circ} hoặc góc ngoài bé hơn 90 ^{\circ}.
• Tam giác nhọn: Là tam giác có ba góc trong nhỏ hơn 90 ^{\circ} hoặc tất cả các góc ngoài lớn hơn 90 ^{\circ}.
• Tam giác đều: Đây là trường hợp đặc biệt của tam giác cân có ba cạnh bằng nhau. Đặc điểm nhận diện của tam giác đều là ba góc bằng nhau và 60 ^{\circ} bằng nhau.
• Tam giác cân: Đây là tam giác có 2 cạnh bằng nhau, hai cạnh này gọi là hai cạnh bên. Đỉnh của tam giác cân là giao điểm của hai cạnh bên. Góc tạo bởi đỉnh gọi là góc đối đỉnh, hai góc còn lại gọi là góc đáy. Tính chất của tam giác cân là hai góc đáy bằng nhau.

Dạng hình tam giác là dạng toán phổ cập so với những em học viên trong quy trình học tập. Dưới đây chúng tôi sẽ ra mắt đến những bạn cách tính diện tích những hình tam giác đơn thuần và thông dụng nhất lúc bấy giờ .

Diện tích tam giác cân

ABC là tam giác cân có 3 cạnh :

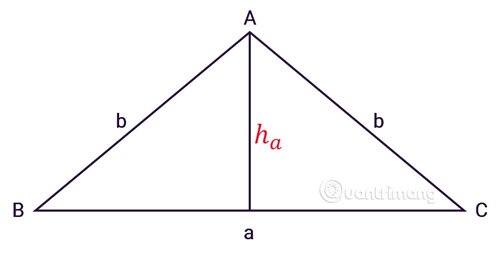
• a là độ dài của cạnh đáy.
• b là độ dài 2 cạnh bên.
• ha là đường cao được tính từ đỉnh A.

Tham khảo công thức tính DT tam giác giác cân :

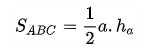
Diện tích tam giác đều

ABC tam giác đều thường có 3 cạnh bằng nhau, A là độ dài của những cạnh .

Tham khảo công thức tính DT tam giác đều :

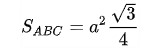
Diện tích tam giác vuông

ABC trong tam giác vuông tại góc B, a và b là độ dài 2 cạnh của góc vuông .

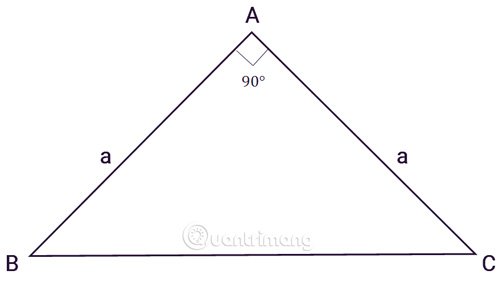
Thường ta sẽ vận dụng công thức tính cho DT tam giác vuông với chiều cao sẽ là 1 trong 2 cạnh góc vuông và cạnh đáy. Tham khảo công thức tính DT tam giác vuông :

Diện tích tam giác vuông cân

ABC trong tam giác vuông cân nằm tại A, a là độ dài 2 cạnh góc vuông :

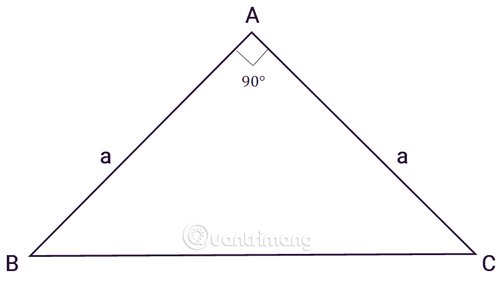
Công thức tính DT tam giác vuông cân với chiều cao và cạnh đáy bằng nhau, tham khảo công thức như sau:

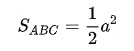
Cho dù vận dụng công thức nào để tính diện tích hình tam giác, học viên nên hiểu rằng không phải khi khi nào chiều cao cũng nằm trong hình tam giác. Bây giờ mới cần vẽ thêm độ cao và cạnh để bổ trợ thêm, khi tính DT hình tam giác quan trọng là phải căn chiều cao ứng với cạnh đáy mà góc nó chiếu xuống .
Chủ đề toán học tương quan :
⇒ Công thức tính diện tích hình tròn trụ
⇒ Công thức tính diện tích hình thoi
⇒ Công thức tính diện tích bình hành
⇒ Công thức tính diện tích hình thang

Đánh Giá post

Source: http://wp.ftn61.com
Category: Thủ Thuật