Hướng dẫn cách tính diện tích tam giác vuông

Tam giác là một trong những hình dạng phổ biến nhất trong đời sống và chúng ta đã được học nhiều về hình học này từ những năm tiểu học với những kiến thức cơ bản nhất. Ngoài chu vi ra thì diện tích tam giác là một yếu tố quan trọng và thường xuyên được nhắc tới trong những bài toán hình học.

Bài viết dưới đây của chúng tôi sẽ giới thiệu tới các bạn các công thức tính diện tích phổ biến từ đơn giản tới nâng cao dành cho các dạng khác nhau của hình tam giác như tam giác vuông, tam giác cân, tam giác đều.

Phân loại tam giác

Mỗi loại tam giác sẽ có những đặc thù khác nhau. Chính thế cho nên mà tất cả chúng ta cần nắm được cách phân loại và đặc thù của từng dạng để vận dụng công thức thống kê giám sát một cách đúng mực và hiệu suất cao nhất .

Tam giác thường

Đây chính là dạng tam giác cơ bản và tổng quát nhất của hình tam giác. Tam giác bao gồm ba cạnh có độ dài khác nhau với số đo ba góc khác nhau nhưng đảm bảo điều kiện tổng của chúng bằng 180 độ.

Hai dạng nhỏ hơn của tam giác thường là tam giác tù và tam giác nhọn .

• Tam giác tù là tam giác có một góc tù lớn hơn 90 độ
• Tam giác nhọn là tam giác mà cả ba góc đều nhỏ hơn 90 độ

Các dạng tam giác đặc biệt quan trọng

• Tam giác cân: Tam giác cân là tam giác có hai cạnh bằng nhau. Hai cạnh này được gọi là hai cạnh bên của tam giác và góc được tạo bởi hai cạnh này gọi là góc ở đỉnh. Hai góc còn lại được góc là hai góc đáy có số đo bằng nhau.
• Tam giác đều: Tam giác đều là trường hợp tam giác có 3 cạnh bằng nhau. Lúc này, tất cả các góc của tam giác sẽ bằng nhau và cùng bằng 60 độ.
• Tam giác vuông: Tam giác vuông là tam giác có 1 góc vuông. Hai cạnh tạo thành góc vuông đó được gọi là cạnh góc vuông và cạnh còn lại được gọi là cạnh huyền. Hai góc còn lại của tam giác sẽ có tổng bằng 90 độ.

• Tam giác vuông cân: Tam giác vuông cân là tam giác có 1 góc vuông và hai cạnh góc vuông có độ dài bằng nhau. Hai góc còn là sẽ có độ lớn bằng nhau và bằng 45 độ.

Công thức tính diện tích tam giác

Sau đây tất cả chúng ta cùng đi vào điểm danh những công thức phổ cập được sử dụng để tính diện tích của những dạng tam giác .

Công thức tính diện tích tam giác thường

Cho hình tam giác ABC với độ dài những cạnh lần lượt là a, b, c như hình và có độ dài đường cao hạ từ đỉnh A là ha và tương tự như với những đỉnh còn lại Ta sẽ có những công thức tính diện tích tam giác như sau :

Công thức tính diện tích tam giác tổng quát

Diện tích của một hình tam giác được tính bằng ½ tích của chiều cao hạ từ đỉnh và độ dài cạnh đối lập của đỉnh đó :

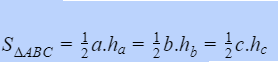
Công thức tính diện tích tam giác khi biết số đo một góc

Trong trường hợp ta chỉ biết độ dài hai cạnh và số đo của góc được tạo thành bởi hai cạnh đó. Ta hoàn toàn có thể vận dụng công thức diện tích tam giác có giá trị bằng ½ tích của độ dài hai cạnh kề về sin của góc được tạo thành bởi 2 cạnh đó :

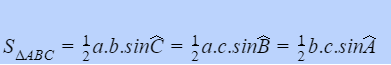
Tính diện tích tam giác bằng công thức Heron

Nếu biết được độ dài 3 cạnh của tam giác, bạn hoàn toàn có thể vận dụng công thức Heron để tính diện tích tam giác :

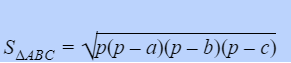
Trong đó : p là nửa chu vi của tam giác có giá trị được xác lập bằng công thức :

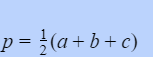
Từ đó, ta hoàn toàn có thể trình diễn lại thành một công thức tổng quát như sau :

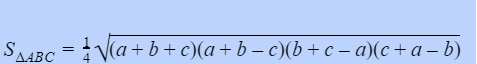
Công thức tính diện tích tam giác bằng bán kính đường tròn ngoại tiếp

Xem thêm: Làm Thế Nào Để Update Win 7 Lên Win 10?

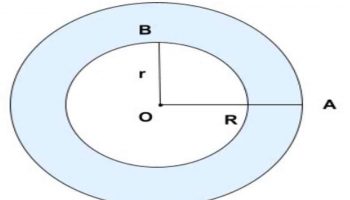
Với đường tròn đã được chứng tỏ là ngoại tiếp tam giác cần tính diện tích, ta hoàn toàn có thể vận dụng 2 công thức sau để tính diện tích của tam giác :

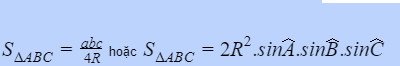
Với R là nửa đường kính đường tròn ngoại tiếp của tam giác ABC cần tính diện tích

Công thức tính diện tích tam giác bằng đường tròn nội tiếp

Nếu có đường tròn nội tiếp tam giác cần tính diện tích với nửa đường kính r, ta hoàn toàn có thể tính được diện tích tam giác bằng công thức sau :

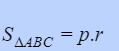
Với p là chu vi hình tam giác .

Công thức tính diện tích tam giác cân

Để hoàn toàn có thể tính được diện tích của tam giác cân, bạn hoàn toàn có thể vận dụng công thức tính diện tích tam giác thường tổng quát :

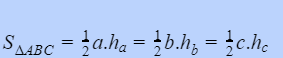
Công thức tính diện tích tam giác đều

Để hoàn toàn có thể tính diện tích tam giác đều một cách nhanh gọn nhất, bạn hoàn toàn có thể vận dụng công thức Heron với dạng rút gọn sau :

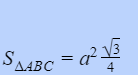
Trong đó a là độ dài những cạnh của tam giác

Công thức tính diện tích tam giác vuông

Đối với tam giác vuông, bạn cũng vận dụng công thức tính diện tích tam giác tổng quát đã được trình làng ở trên. Tuy nhiên vì đã có hai cạnh góc vuông nên bạn không cần phải xác lập độ dài đường cao của tam giác nữa mà hoàn toàn có thể vận dụng ngay công thức tính .

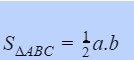
Trong đó : a, b là độ dài hai cạnh góc vuông của tam giác

Tương tự với trường hợp đặc biệt là tam giác vuông cân, bạn chỉ cần áp dụng công thức trên là có thể tính được diện tích tam giác một cách nhanh chóng. Điểm đặc biệt của tam giác vuông cân là hai cạnh góc vuông sẽ có độ dài bằng nhau, chính vì vậy công thức có thể được viết lại như sau:

Hy vọng bài viết trên đây của chúng tôi đã giúp bạn có thể vận dụng được hiệu quả các công thức tính diện tích hình tam giác một cách nhanh chóng và hiệu quả. Nếu bạn muốn đọc thêm những bài viết có nội dung tương tự, đừng quên thường xuyên truy cập vào website thosuaxe.info để không bỏ lỡ những kiến thức mới nhất nhé!

Xem thêm:

Source: http://wp.ftn61.com
Category: Thủ Thuật