Công thức giải bất phương trình và bài tập có lời giải từ A – Z

Trong bài viết dưới đây, điện máy Sharp Việt Nam tổng hợp các công thức giải bất phương trình và các dạng bài tập về bất phương trình có lời giải chi tiết giúp các bạn ôn lại kiến thức để làm bài tập nhanh chóng nhé

A. Bất phương trình quy về bậc nhất

Trong phần A, điện máy Sharp Nước Ta sẽ trình làng những công thức giải bất phương trình lớp 10 dành cho những phương trình bậc nhất. Trước khi đi vào những công thức giải những em cần phải nắm vững bảng xét dấu của nhị thức bậc nhất .

Lưu ý: Phải cùng trái khác

Giải và biện luận bất phương trình dạng ax + b < 0

Điều kiện		Kết quả tập nghiệm
a > 0		S = ( – ∞, -b/a)
a < 0		S = ( -b/a, + ∞)
a = 0	b ≥ 0	S = ∅
	b < 0	S= R

Hệ bất phương trình bậc nhất một ẩn

Muốn giải hệ bất phương trình bậc nhất một ẩn ta giải từng bất phương trình của hệ rồi lấy giao những tập nghiệm thu sát hoạch được .

Dấu nhị thức bậc nhất

f(x) = ax + b (a ≠ 0)
x ∈ ( – ∞, -b/a)	a.f(x) < 0
x ∈ ( -b/a, + ∞)	a.f(x) > 0

Bất phương trình tích

Dạng : P ( x ). Q ( x ) > 0 ( 1 ) ( trong đó P ( x ), Q. ( x ) là những nhị thức bậc nhất. )
∙ Cách giải : Lập bxd của P ( x ). Q ( x ). Từ đó suy ra tập nghiệm của ( 1 ) .

Bất phương trình chứa ẩn ở mẫu

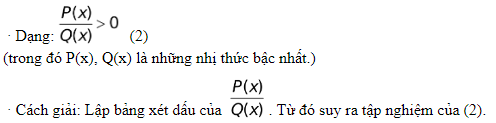
Chú ý : Không nên qui đồng và khử mẫu .

Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối

Tương tự như giải pt chứa ẩn trong dấu giá trị tuyệt đối, ta hay sử dụng định nghĩa và đặc thù của giá trị tuyệt đối để khử dấu giá trị tuyệt đối .

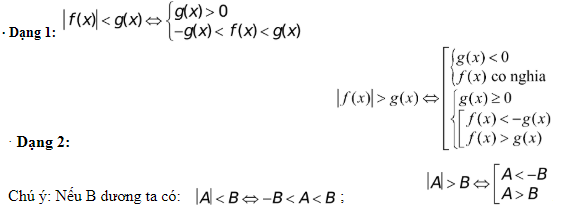
Tham khảo thêm: 

B. Bất phương trình quy về bậc hai

Trong phần B, diện máy Sharp Nước Ta sẽ liên tục ra mắt những công thức giải bất phương trình lớp 10 dành cho những phương trình bậc hai và phương trình qui về bậc hai. Trước khi đi vào những công thức giải những em cần phải nắm vững bảng xét dấu của nhị thức bậc nhất .

Dấu của tam thức bậc hai

f(x) = ax2 + bx + c ( a ≠ 0)
Δ > 0	a.f(x) > 0, ∀x ∈ R
Δ = 0	a.f(x) > 0, ∀x ∈ R \ {-b/2a}
Δ < 0	a.f(x) > 0, ∀x ∈ ( -∞, x1) ∪ (x2, +∞)
	a.f(x) < 0, ∀x ∈ ( x1, x2)

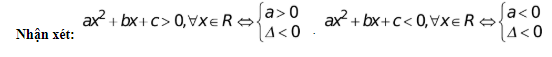
Bất phương trình bậc hai một ẩn ax2 + bx + c > 0 (hoặc ≥ 0; < 0; ≤ 0)

Để giải bất phương trình bậc hai ta vận dụng định lí về dấu của tam thức bậc hai .

Phương trình – Bất phương trình chứa ẩn trong dấu giá trị tuyệt đối

Để giải phương trình, bất phương trình chứa ẩn trong dấu giá trị tuyệt đối, ta thường sử dụng định nghĩa hoặc đặc thù của giá trị tuyệt đối để khử dấu giá trị tuyệt đối .

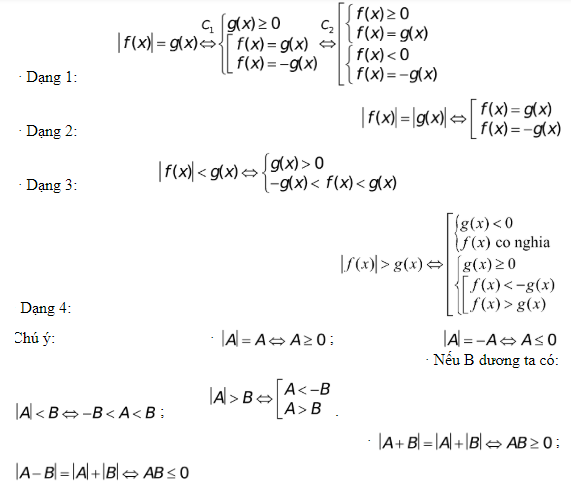
Phương trình – Bất phương trình chứa ẩn trong dấu căn

Trong những dạng toán thì bất phương trình chứa căn được xem là dạng toán khó nhất. Để giải phương trình, bất phương trình chứa ẩn trong dấu căn ta cầ sử dụng phối hợp những công thức giải bất phương trình lớp 10 tích hợp với phép nâng luỹ thừa hoặc đặt ẩn phụ để khử dấu căn .

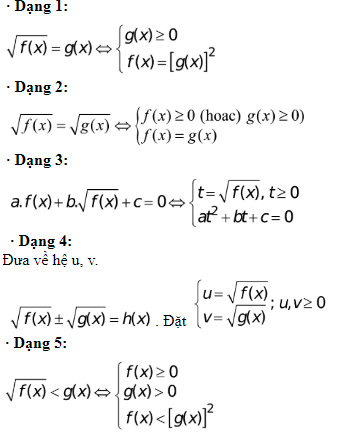
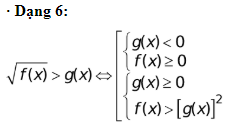
Bài tập về giải bất phương trình lớp 10 có lời giải

Ví dụ 1 : Cho bất phương trình 2 x ≤ 3 .
a ) Trong những số – 2 ; 2 ½ ; π ; √ 10 số nào là nghiệm, số nào không là nghiệm của bất phương trình trên ?
b ) Giải bất phương trình đó và biểu diễn tập nghiệm của nó trên trục số .
Lời giải
a ) Ta có : 2. ( – 2 ) ≤ 3 nên – 2 có là nghiệm của bất phương trình

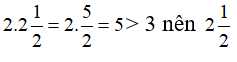 không là nghiệm của bất phương trình ,

2 π > 3 nên π không là nghiệm của bất phương trình .
2 √ 10 > 3 ( vì 40 > 9 ) nên √ 10 không là nghiệm của bất phương trình ,
Các số là nghiệm của bất phương trình trên là : – 2 ;
Các số không là nghiệm của bất phương trình trên là : 2 ½ ; π ; √ 10
b ) 2 x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là :

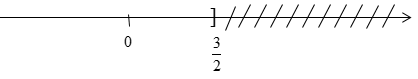
Ví dụ 2 : Tìm những giá trị x thỏa mãn nhu cầu điều kiện kèm theo của mỗi bất phương trình sau :

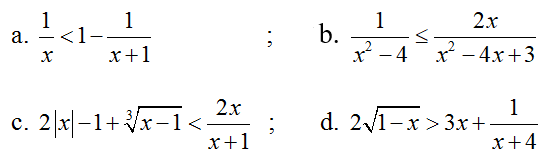
Lời giải

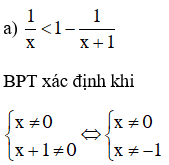
Vậy tập giá trị của x thỏa mãn nhu cầu điều kiện kèm theo xác lập là D = R \ { 0 ; – 1 }

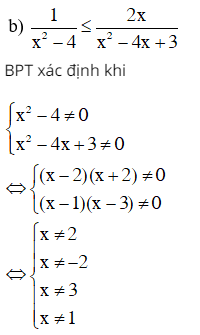
Vậy tập giá trị của x thỏa mãn nhu cầu điều kiện kèm theo xác lập là D = R \ { – 2 ; 1 ; 2 ; 3 }

Ví dụ 3 : Chứng minh những bất phương trình sau vô nghiệm :

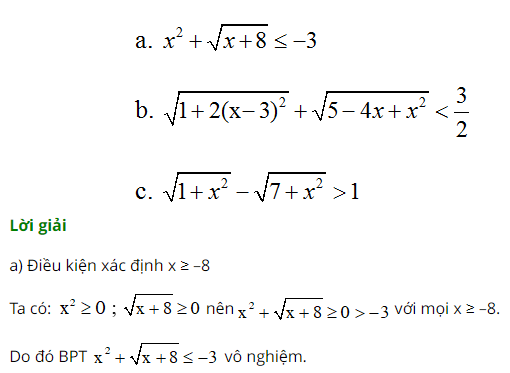
b ) Tập xác lập : D = R .

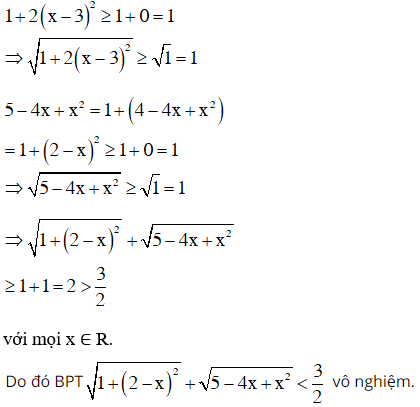
c ) Tập xác lập D = R .
Ta có :

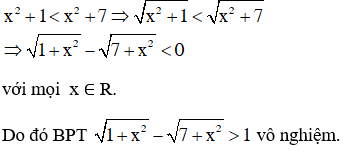
Ví dụ 4 : Giải thích vì sao những cặp bất phương trình sau tương tự ?
a ) – 4 x + 1 > 0 và 4 x – 1 < 0 b ) 2x2 + 5 ≤ 2 x – 1 và 2x2 – 2 x + 6 ≤ 0 Lời giải

a) Nhân hai vế của BPT: –4x + 1 > 0 với (–1) < 0 ta được BPT: 4x – 1 < 0 nên hai BPT đó tương đương.

Viết là – 4 x + 1 > 0 ⇔ 4 x – 1 < 0 . b ) Ta có : 2x2 + 5 ≤ 2 x – 1 ⇔ 2x2 + 5 + 1 – 2 x ≤ 2 x – 1 + 1 – 2 x ( Cộng cả hai vế của BPT với 1 – 2 x ) . ⇔ 2x2 – 2 x + 6 ≤ 0 . Vậy hai BPT đã cho tương tự : 2x2 + 5 ≤ 2 x – 1 ⇔ 2x2 – 2 x + 6 ≤ 0 . Ví dụ 5 : Giải những bất phương trình sau :

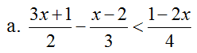
b. ( 2 x – 1 ) ( x + 3 ) – 3 x + 1 ≤ ( x – 1 ) ( x + 3 ) + x2 – 5
Lời giải
a ) Tập xác lập D = R .

b ) ( 2 x – 1 ) ( x + 3 ) – 3 x + 1 ≤ ( x – 1 ) ( x + 3 ) + x2 – 5
⇔ 2×2 + 6 x – x – 3 – 3 x + 1 ≤ x2 + 3 x – x – 3 + x2 – 5
⇔ 2×2 + 2 x – 2 ≤ 2×2 + 2 x – 8
⇔ 6 ≤ 0 ( Vô lý ) .
Vậy BPT vô nghiệm .
Ví dụ 6 : Biểu diễn hình học tập nghiệm của những bất phương trình bậc nhất hai ẩn sau :
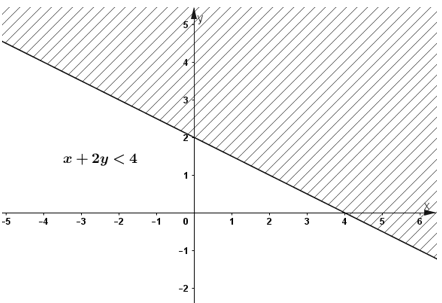
a ) – x + 2 + 2 ( y – 2 ) < 2 ( 1 – x ) b ) 3 ( x – 1 ) + 4 ( y – 2 ) < 5 x – 3 Lời giải a ) – x + 2 + 2 ( y – 2 ) < 2 ( 1 – x ) ⇔ – x + 2 + 2 y – 4 < 2 – 2 x ⇔ x + 2 y < 4 ( 1 ) Biểu diễn tập nghiệm trên mặt phẳng tọa độ : – Vẽ đường thẳng x + 2 y = 4 . – Thay tọa độ ( 0 ; 0 ) vào ( 1 ) ta được 0 + 0 < 4 ⇒ ( 0 ; 0 ) là một nghiệm của bất phương trình . Vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa gốc tọa độ không kể bờ với bờ là đường thẳng x + 2 y = 4 ( miền không bị gạch ) .

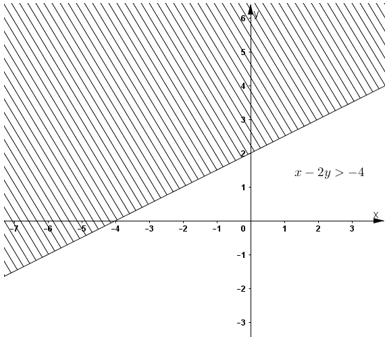
b ) 3 ( x – 1 ) + 4 ( y – 2 ) < 5 x – 3 ⇔ 3 x – 3 + 4 y – 8 < 5 x – 3 ⇔ - 2 x + 4 y < 8 ⇔ x – 2 y > – 4 ( chia cả hai vế cho – 2 < 0 ) ( 2 ) Biểu diễn tập nghiệm trên mặt phẳng tọa độ : – Vẽ đường thẳng x – 2 y = – 4 . – Thay tọa độ ( 0 ; 0 ) vào ( 2 ) ta được : 0 + 0 > – 4 đúng
⇒ ( 0 ; 0 ) là một nghiệm của bất phương trình .
Vậy miền nghiệm của bất phương trình là nửa mặt phẳng chứa gốc tọa độ không kể bờ với bờ là đường thẳng x – 2 y = – 4

Bên trên chính là hàng loạt những công thức giải bất phương trình lớp 10 hoàn toàn có thể giúp những bạn học viên mạng lưới hệ thống lại kỹ năng và kiến thức để vận dụng vào làm bài tập nhé

Đánh giá bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp