Giải hệ phương trình bằng phương pháp cộng đại số chuẩn 100%

Trong bài viết này, chúng tôi sẽ hướng dẫn các bạn cách giải hệ phương trình bằng phương pháp cộng đại số giúp các bạn hệ thống lại kiến thức từ đó áp dụng giải bài toán bằng phương pháp nhanh chóng và chính xác nhất nhé. Nào chúng ta cùng bắt đầu thôi nào.

Hướng dẫn cách giải hệ phương trình bằng phương pháp cộng đại số

Quy tắc cộng đại số dùng để biến hóa một hệ phương trình thành hệ phương trình tương tự. Quy tắc cộng đại số gồm hai bước :

1. Quy tắc cộng đại số

Quy tắc cộng đại số dùng để đổi khác một hệ phương trình thành hệ phương trình tương tự. Quy tắc cộng đại số gồm hai bước :

• Bước 1: Cộng hay trừ từng vế hai phương trình của hệ phương trình đã cho để được một phương trình mới.
• Bước 2: Dùng phương trình mới ấy thay thế cho một trong hai phương trình của hệ (và giữ nguyên phương trình kia) ta được hệ phương trình mới tương đương với hệ đã cho.

2. Cách giải hệ phương trình bằng phương pháp cộng đại số

• Bước 1: Nhân các vế của hai phương trình với số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình của hệ bằng nhau hoặc đối nhau.
• Bước 2: Sử dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
• Bước 3: Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho.

Tham khảo thêm:

Bài tập giải hệ phương trình bằng phương pháp cộng đại số

Ví dụ 1 : Giải các hệ phương trình sau

Lời giải :
a, Cộng từng vế hai phương trình đã cho ta được :
( 2 x + x ) + ( y – y ) = 3 = 6 ⇔ 3 x = 9 do đó hệ phương trình tương tự với

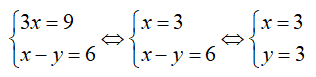
Vậy hệ phương trình có nghiệm duy nhất ( x, y ) = ( 3 ; 3 )
b ,

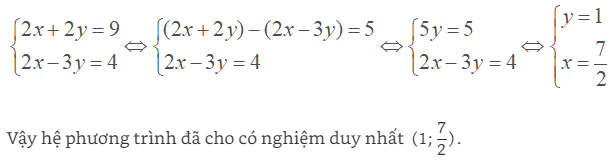
Ví dụ 2 : Giải các hệ phương trình sau

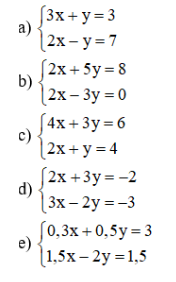
Lời giải :

Ví dụ 3 : Giải hệ phương trình sau :

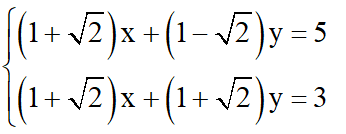
Lời giải
Lấy phương trình ( 2 ) trừ phương trình ( 1 ), vế trừ vế ta được :

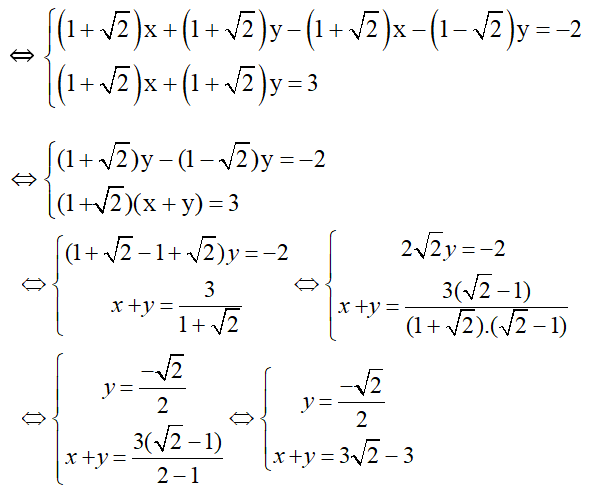
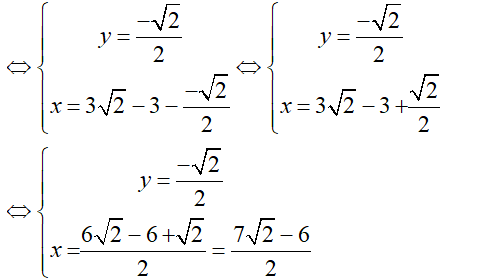
Vậy nghiệm duy nhất là

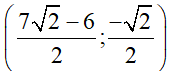
Lưu ý :

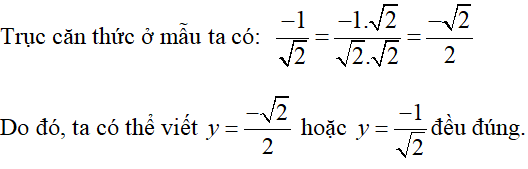
Ví dụ 4 : Giải các hệ phương trình sau

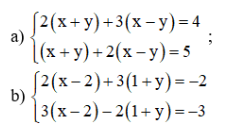
Lời giải
Bài toán này có hai cách giải :

• Cách 1: Thu gọn từng phương trình ta sẽ thu được phương trình bậc nhất hai ẩn x và y.
• Cách 2: Đặt ẩn phụ.

Cách 1:

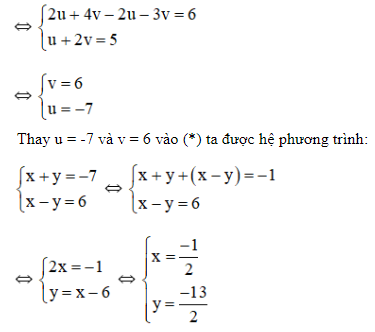
• u = -1 ⇒x –2 = -1 ⇒x = 1
• v = 0 ⇒y + 1 = 0 ⇒y = -1.

Vậy hệ phương trình có nghiệm ( 1 ; – 1 )
Tóm lại : với chiêu thức giải hệ phương trình bằng chiêu thức cộng đại số sẽ không làm phát sinh phân số như giải pháp thế điều này giúp các bạn đỡ nhầm lẫn khi giải hệ

Đánh giá bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp