Sách Giải Bài Tập Toán Lớp 8 Bài 7: Giải Bài Toán Bằng Cách Lập Phương Trình (tiếp) – Luyện Tập (trang 31-32)

Xem toàn bộ tài liệu Lớp 8: tại đây

Xem thêm các sách tham khảo liên quan:

Sách giải toán 8 Bài 7 : Giải bài toán bằng cách lập phương trình ( tiếp ) – Luyện tập ( trang 31-32 ) giúp bạn giải các bài tập trong sách giáo khoa toán, học tốt toán 8 sẽ giúp bạn rèn luyện năng lực suy luận hài hòa và hợp lý và hợp logic, hình thành năng lực vận dụng kết thức toán học vào đời sống và vào các môn học khác :

Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28: Trong Ví dụ trên, hay thử chọn ẩn số theo cách khác: Gọi s (km) là quãng đường từ Hà Nội đến điểm gặp nhau của hai xe. Điền vào bảng sau rồi lập phương trình với ẩn số s:

	Vận tốc (km/h)	Quãng đường đi (km)	Thời gian đi (h)
Xe máy		s
Ô tô

Lời giải

	Vận tốc (km/h)	Quãng đường đi (km)	Thời gian đi (h)
Xe máy	35	s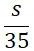
Ô tô	45	90 – s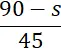

Ô tô xuất phát sau xe máy 2/5 giờ nên

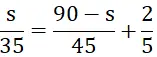
Trả lời câu hỏi Toán 8 Tập 2 Bài 7 trang 28: Giải phương trình nhận được rồi suy ra đáp số của bài toán. So sánh hai cách chọn ẩn, em thấy cách nào cho lời giải gọn hơn ?

Lời giải

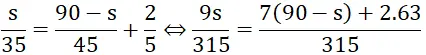
⇔ 9 s = 7 ( 90 – s ) + 126
⇔ 9 s = 756 – 7 s
⇔ 16 s = 756
⇔ s = 47,25 ( km )
Thời gian để hai xe gặp nhau từ lúc xe máy khởi hành là :

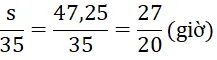
Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Bài 37 (trang 30 SGK Toán 8 tập 2): Lúc 6 giờ sáng, một xe máy khởi hành từ A để đến B. Sau đó 1 giờ, một ô tô cũng xuất phát từ A đến B với vận tốc trung bình lớn hơn vận tốc trung bình của xe máy 20km/h. Cả hai xe đến B đồng thời vào lúc 9 giờ 30 phút sáng cùng ngày. Tính độ dài quãng đường AB và vận tốc trung bình của xe máy.

Lời giải:

* Phân tích bài toán:

Chọn x là tốc độ trung bình của xe máy .
( Các bạn hoàn toàn có thể chọn x là quãng đường AB và làm tựa như ) .

	Thời gian	Vận tốc	Quãng đường AB
Xe máy	3,5	x	3,5x
Ô tô	2,5	x + 20	2,5(x + 20).

* Giải:

Gọi tốc độ trung bình của xe máy là x ( x > 0, km / h ) .
Thời gian xe máy đi từ A đến B : 9 h30 – 6 h = 3,5 ( h ) .
Quãng đường AB ( tính theo xe máy ) là : 3,5. x ( km ) .
Vận tốc trung bình của xe hơi lớn hơn tốc độ trung bình của xe máy 20 km / h
⇒ Vận tốc trung bình của xe hơi là : x + 20 ( km / h )
Ô tô xuất phát sau xe máy 1 h
⇒ thời hạn xe hơi đi từ A đến B là : 3,5 – 1 = 2,5 ( h ) .
Quãng đường AB ( tính theo xe hơi ) là : 2,5 ( x + 20 ) ( km )
Ta có phương trình : 3,5 x = 2,5 ( x + 20 ) ⇔ 3,5 x = 2,5 x + 50 ⇔ x = 50 ( thỏa mãn nhu cầu ) .
⇒ Quãng đường AB : 3,5. 50 = 175 ( km ) .
Vậy quãng đường AB dài 175 km và tốc độ trung bình của xe máy là 50 km / h .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Bài 38 (trang 30 SGK Toán 8 tập 2): Điểm kiểm tra Toán của một tổ học tập được cho trong bảng sau:

Biết điểm trung bình của cả tổ là 6,6. Hãy điền các giá trị thích hợp vào hai ô còn trống ( được lưu lại * ) .

Lời giải:

Gọi x là số học viên ( tần số ) được điểm 5 ( 0 < x < 10 ; nguyên ) . Tần số hay số học viên được điểm 9 là : 10 – ( 1 + 2 + 3 + x ) = 4 – x Điểm trung bình của cả tổ bằng 6,6 điểm nên :

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Bài 39 (trang 30 SGK Toán 8 tập 2): Lan mua hai loại hàng và phải trả tổng cộng 120 nghìn đồng, trong đó đã tính cả 10 nghìn đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với loại hàng thứ nhất là 10%; thuế VAT đối với loại hàng thứ 2 là 8%. Hỏi nếu không kể thuế VAT thì Lan phải trả mỗi loại hàng bao nhiêu tiền?

Ghi chú: Thuế VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Gỉa sử thuế VAT đối với mặt hàng A được quy định là 10%. Khi đó nếu giá bán của A là a đồng thì kể cả thuế VAT, người mua mặt hàng này phải trả tổng cộng là a + 10% a đồng.

Lời giải:

* Phân tích:

Vì trong 120 nghìn Lan trả có 10 nghìn thuế Hóa Đơn đỏ VAT nên giá gốc của hai loại sản phẩm không tính Hóa Đơn đỏ VAT là 110 nghìn đồng .

	Giá gốc	Thuế VAT
Hàng thứ 1	x	0,1.x
Hàng thứ 2	110 – x	0,08.(110 – x)

Thuế Hóa Đơn đỏ VAT của cả hai mẫu sản phẩm là 10 nghìn nên có phương trình :
0,1 x + 0,08 ( 110 – x ) = 10 .

* Giải

Gọi giá gốc của mẫu sản phẩm thứ nhất là x ( 0 < x < 120 nghìn đồng ) . Vì trong 120 nghìn đồng Lan trả đã có 10 nghìn đồng thuế Hóa Đơn đỏ VAT nên tổng giá gốc của cả hai mẫu sản phẩm chỉ bằng : 120 – 10 = 110 ( nghìn đồng ) . ⇒ Giá gốc của loại sản phẩm thứ hai là : 110 – x ( nghìn đồng ) . Thuế Hóa Đơn đỏ VAT của loại sản phẩm thứ nhất bằng : 10 %. x = 0,1 x . Thuế Hóa Đơn đỏ VAT của loại sản phẩm thứ hai bằng : 8 %. ( 110 – x ) = 0,08. ( 110 – x ) . Thuế Hóa Đơn đỏ VAT của cả hai loại sản phẩm bằng : 0,1 x + 0,08 ( 110 – x ) ( nghìn đồng ) . Theo đề bài, tổng thuế Hóa Đơn đỏ VAT của cả hai mẫu sản phẩm là 10 nghìn đồng nên ta có phương trình : 0,1 x + 0,08 ( 110 – x ) = 10 ⇔ 0,1 x + 8,8 – 0,08 x = 10 ⇔ 0,02 x = 1,2 ⇔ x = 60 ( thỏa mãn nhu cầu điều kiện kèm theo ) . Vậy không kể Hóa Đơn đỏ VAT thì giá của mẫu sản phẩm thứ nhất là 60 nghìn đồng, giá của loại sản phẩm thứ hai là 110 – 60 = 50 nghìn đồng .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 40 (trang 31 SGK Toán 8 tập 2)Năm nay, tuổi mẹ gấp 3 lần tuổi Phương. Phương tính rằng 13 năm nữa thì tuổi mẹ chỉ còn gấp 2 lần tuổi Phương thôi. Hỏi năm nay Phương bao nhiêu tuổi?

Lời giải:

* Phân tích :

	Tuổi Phương	Tuổi mẹ
Năm nay	x	3x
13 năm sau	x + 13	3x + 13

Sử dụng dữ kiện 13 năm sau tuổi mẹ chỉ gấp hai lần tuổi Phương nên ta có phương trình :
3 x + 13 = 2 ( x + 13 )
* Giải :
Gọi x là tuổi Phương năm nay ( x > 0 ; x ∈ N )
Tuổi của mẹ năm nay là : 3 x
Tuổi Phương 13 năm sau : x + 13
Tuổi của mẹ 13 năm sau : 3 x + 13

13 năm nữa tuổi mẹ chỉ gấp 2 lần tuổi Phương nên ta có phương trình :
3 x + 13 = 2 ( x + 13 )
⇔ 3 x + 13 = 2 x + 26
⇔ x = 13 ( thỏa mãn nhu cầu điều kiện kèm theo xác lập )
Vậy năm nay Phương 13 tuổi .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 41 (trang 31 SGK Toán 8 tập 2): Một số tự nhiên có hai chữ số. Chữ số hàng đơn vị gấp hai lần chữ số hàng chục. Nếu thêm chữ số 1 xen vào giữa hai chữ số ấy thì được một số mới lớn hơn số ban đầu 370. Tìm số ban đầu.

Lời giải:

* Phân tích:

Với một số có hai chữ số bất kì ta luôn có: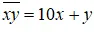

Khi thêm chữ số 1 xen vào giữa ta được số: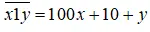

Vì chữ số hàng đơn vị chức năng gấp 2 lần chữ số hàng chục nên ta có y = 2 x .
Số mới lớn hơn số bắt đầu 370 nên ta có phương trình :
100 x + 10 + 2 x = 10 x + 2 x + 370 .

* Giải:

Gọi chữ số hàng chục của số cần tìm là x ( x > 0, x ∈ N ) .
⇒ Chữ số hàng đơn vị chức năng là 2 x
⇒ Số cần tìm bằng

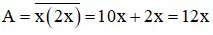
Sau khi viết thêm chữ số 1 vào giữa hai chữ số ta được số mới là :

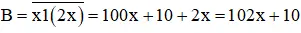
Theo đề bài ta có B = A + 370 nên ta có phương trình
102 x + 10 = 12 x + 370
⇔ 102 x – 12 x = 370 – 10
⇔ 90 x = 360
⇔ x = 4 ( thỏa mãn nhu cầu )
Vậy số cần tìm là 48 .
* Lưu ý : Vì chỉ có 4 số có hai chữ số thỏa mãn nhu cầu điều kiện kèm theo chữ số hàng đơn vị chức năng gấp đôi chữ số hàng chục là : 12 ; 24 ; 36 ; 48 nên ta hoàn toàn có thể đi thử trực tiếp mà không cần giải bằng cách lập phương trình .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 42 (trang 31 SGK Toán 8 tập 2): Tìm số tự nhiên có hai chữ số, biết rằng nếu viết thêm một chữ số 2 vào bên trái và một chữ số 2 vào bên phải số đó thì ta được một số lớn hơn gấp 153 lần số ban đầu.

Lời giải:

Gọi số có hai chữ số cần tìm là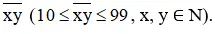

Khi viết thêm một chữ số 2 vào bên trái và một chữ số 2 vào bên phải thì ta được số mới là

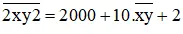
Theo đề bài, số mới gấp 153 lần số bắt đầu nên ta có phương trình :

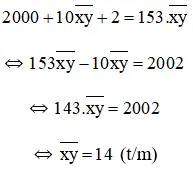
Vậy số cần tìm là 14 .

* Lưu ý : Ở bài toán này ta coi cả số 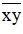là một ẩn.

Các bạn hoàn toàn có thể đặt ẩn đơn thuần là x hoặc A … nhưng khi phân tích số
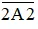thì các bạn cần lưu ý nó là số có 4 chữ số nên 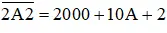, nếu bạn phân tích thành 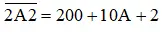là sai.
thì các bạn cần quan tâm nó là số có 4 chữ số nên, nếu bạn nghiên cứu và phân tích thànhlà sai .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 43 (trang 31 SGK Toán 8 tập 2): Tìm phân số có đồng thời các tính chất sau:

a) Tử số của phân số là số tự nhiên có một chữ số;

b ) Hiệu giữa tử số và mẫu số bằng 4 ;
c ) Nếu giữ nguyên tử số và viết thêm vào bên phải của mẫu số một chữ số đúng bằng tử số, thì ta được một phân số bằng phân số 1/5 .

Lời giải:

Gọi tử số của phân số cần tìm là x ( 0 < x < 10, x ∈ N ) . + Tử số là số tự nhiên có một chữ số nên ta có điều kiện kèm theo 0 < x < 10 . + Hiệu giữa tử số và mẫu số bằng 4 nên mẫu số bằng x – 4 .

+ Viết thêm chữ số đúng bằng tử số vào bên phải của mẫu số ta được mẫu số mới là: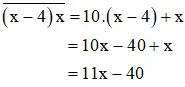

Phân số mới bằng 1/5 nên ta có phương trình :

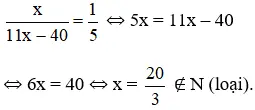
Vậy không có phân số thỏa mãn nhu cầu nhu yếu đề bài .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 44 (trang 31 SGK Toán 8 tập 2): Điểm kiểm tra Toán của một lớp được cho trong bảng dưới đây:

Điểm (x)	1	2	3	4	5	6	7	8	9	10
Tần số (f)	0	0	2	*	10	12	7	6	4	1	N = *

trong đó có 2 ô còn trống ( thay bằng dấu * ). Hãy điền số thích hợp vào ô trống, nếu điểm trung bình của lớp là 6,06 .

Lời giải:

Gọi x là tần số của điểm 4 ( x > 0 ; x ∈ N )
Số học sinh của lớp :
2 + x + 10 + 12 + 7 + 6 + 4 + 1 = 42 + x
Vì điểm trung bình bằng 6,06 nên :

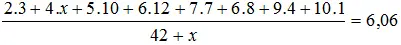
⇔ 6 + 4 x + 50 + 72 + 49 + 48 + 36 + 10 = 6,06 ( 42 + x )
⇔ 271 + 4 x = 254,52 + 6,06 x ⇔ 16,48 = 2,06 x
⇔ x = 8 ( thỏa mãn nhu cầu điều kiện kèm theo đặt ra )
Vậy ta có hiệu quả điền vào như sau :

Điểm (x)	1	2	3	4	5	6	7	8	9	10
Tần số (f)	0	0	2	8	10	12	7	6	4	1	N = 50

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 45 (trang 31 SGK Toán 8 tập 2): Một xí nghiệp kí hợp đồng dệt một số tấm thảm len trong 20 ngày. Do cải tiến kĩ thuật, năng suất dệt của xí nghiệp đã tăng 20%. Bởi vậy, chỉ trong 18 ngày, không những xí nghiệp đã hoàn thành số thảm cần dệt mà còn dệt thêm được 24 tấm nữa. Tính số tấm thảm len mà xí nghiệp phải dệt theo hợp đồng.

Lời giải:

Cách 1:

* Phân tích :
Ta có : Số mẫu sản phẩm dệt được = hiệu suất. số ngày dệt .

	Năng suất	Số ngày dệt	Tổng sản phẩm
Dự tính	x	20	20.x
Thực tế sau khi cải tiến	x + 20%.x = 1,2x	18	18.1,2.x

Thực tế dệt được nhiều hơn dự trù 24 tấm nên ta có phương trình :
18.1,2 x = 20 x + 24
* Giải :
Gọi x là hiệu suất dự trù của xí nghiệp sản xuất ( x > 0, loại sản phẩm / ngày ) .
⇒ Số thảm len dệt được theo dự trù là : 20 x ( thảm ) .
Sau khi nâng cấp cải tiến, hiệu suất của xí nghiệp sản xuất đã tăng 20 % nên hiệu suất trên thực tiễn là : x + 20 %. x = x + 0,2 x = 1,2 x ( mẫu sản phẩm / ngày ) .
Sau 18 ngày, xí nghiệp sản xuất dệt được : 18.1,2 x = 21,6. x ( thảm ) .
Vì sau 18 ngày, xí nghiệp sản xuất không những hoàn thành xong số thảm cần dệt mà còn dệt thêm được 24 tấm nên ta có phương trình :
21,6. x = 20 x + 24
⇔ 21,6 x – 20 x = 24
⇔ 1,6 x = 24
⇔ x = 15 ( thỏa mãn nhu cầu )
Vậy số thảm mà nhà máy sản xuất phải dệt khởi đầu là : 20.15 = 300 ( thảm ) .

Cách 2:

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 46 (trang 31-32 SGK Toán 8 tập 2): Một người lái ô tô dự định đi từ A đến B với vận tốc 48km/h. Nhưng sau khi đi được 1 giờ với vận tốc ấy, ô tô bị tàu hỏa chắn đường trong 10 phút. Do đó, để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm 6km/h. Tính quãng đường AB.

Lời giải:

* Phân tích :
Ta luôn có : Quãng đường = tốc độ. thời hạn

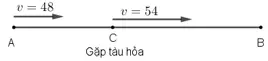
Gọi C là khu vực xe hơi gặp tàu hỏa .
Quãng đường AC xe hơi vẫn đi với tốc độ 48 km / h trong 1 h nên AC = 48 km .
Xét trên quãng đường BC, xe hơi dự trù vẫn đi với tốc độ 48 km / h nhưng gặp tàu hỏa nên trong trong thực tiễn xe hơi đi với tốc độ 48 + 6 = 54 ( km / h ) .
Vì xe hơi đến B đúng thời hạn đã định nên thời hạn thực tiễn xe hơi đi từ B đến C ít hơn thời hạn dự tính là 10 phút = 1/6 giờ ( là thời hạn chờ tàu hỏa ) .

	Quãng đường BC	Vận tốc	Thời gian
Dự tính	x	48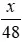
Thực tế	x	48 + 6 = 54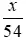

Ta có phương trình: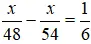

* Giải :

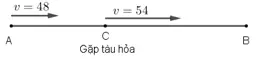
Gọi C là khu vực xe hơi gặp tàu hỏa .

Quãng đường AC xe hơi đi với tốc độ 48 km / h và đi trong 1 giờ
⇒ AC = 48.1 = 48 ( km ) .
Gọi quãng đường BC là x ( x > 0, km ) .
Vận tốc dự trù đi trên BC là : 48 km / h

⇒ Thời gian dự tính đi quãng đường BC hết: 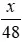(giờ).

Thực tế xe hơi đi quãng đường BC với tốc độ bằng 48 + 6 = 54 ( km / h ) .

⇒ Thời gian thực tế ô tô đi quãng đường BC là: 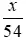(giờ).

Thời gian chênh nhau giữa dự trù và trong thực tiễn chính là thời hạn xe hơi đợi tàu hỏa là 10 phút = 1/6 ( giờ ) .

Do đó ta có phương trình: 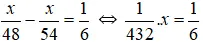⇔ x = 72 (thỏa mãn).

Vậy quãng đường AB = AC + BC = 48 + 72 = 120 ( km ) .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 47 (trang 32 SGK Toán 8 tập 2): Bà An gửi vào quỹ tiết kiệm x nghìn đồng với lãi suất mỗi tháng là a% (a là một số cho trước) và lãi tháng này được tính gộp vào vốn cho tháng sau.

a ) Hãy viết biểu thức biểu lộ :
+ Số tiền lãi sau tháng thứ nhất ;
+ Số tiền ( cả gốc lẫn lãi ) có được sau tháng thứ nhất ;
+ Tổng số tiền lãi có được sau tháng thứ hai .
b ) Nếu lãi suất vay là 1,2 % ( tức là a = 1,2 ) và sau 2 tháng tổng số tiền lãi là 48,288 nghìn đồng, thì lúc đầu bà An đã gửi bao nhiêu tiền tiết kiệm ngân sách và chi phí ?

Lời giải:

a ) Bà An gửi vào quỹ tiết kiệm ngân sách và chi phí : x đồng
Lãi suất là a % tháng nên số tiền lãi sau tháng thứ nhất bằng : a %. x
Số tiền có được sau tháng thứ nhất : x + a %. x = ( 1 + a % ) x
Số tiền lãi sau tháng thứ hai : ( 1 + a % ) x. a %
Tổng số tiền lãi sau hai tháng bằng : a %. x + ( 1 + a % ). x. a % ( đồng ) ( 1 )
b ) Vì sau hai tháng bà An lãi 48288 đồng với lãi suất vay 1,2 % ( tức là a = 1,2 ) nên thay vào ( 1 ) ta có phương trình :
1,2 %. x + ( 1 + 1,2 % ). x. 1,2 % = 48288
⇔ 0,012 x + 1,012. x. 0,012 = 48288
⇔ 0,024144. x = 48288
⇔ x = 2 000 000 ( đồng ) .
Vậy bà An đã gửi tiết kiệm chi phí 2 000 000 đồng .

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 48 (trang 32 SGK Toán 8 tập 2): Năm ngoái, tổng số dân của hai tỉnh A và B là 4 triệu. Năm nay, dân số của tỉnh A tăng thêm 1,1%, còn dân số của tỉnh B tăng thêm 1,2%. Tuy vậy số dân của tỉnh A năm nay vẫn nhiều hơn tỉnh B là 807200 người. Tính số dân năm ngoái của mỗi tỉnh.

Lời giải:

* Phân tích:

	Năm ngoái	Năm nay
Tỉnh A	x	x + x.1,1% = 1,011.x
Tỉnh B	4 – x	(4 – x) + (4 – x).1,2% = (4 – x).1,012

Dân số tỉnh A năm nay nhiều hơn dân số tỉnh B là 807200 người = 0,8072 ( triệu người ) nên ta có phương trình :
1,011. x – 1,012. ( 4 – x ) = 0,8072 .

* Giải:

Gọi x là số dân năm ngoái của tỉnh A ( 0 < x < 4 ; triệu người ) Số dân năm ngoái của tỉnh B : 4 – x ( triệu người ) . Số dân của tỉnh A năm nay : x + 1,1 % x = 1,011. x Số dân của tỉnh B năm nay : ( 4 – x ) + 1,2 % ( 4 – x ) = 1,012 ( 4 – x ) Vì số dân tỉnh A năm nay hơn tỉnh B là 807200 người = 0,8072 triệu người nên ta có phương trình : 1,011. x – 1,012 ( 4 – x ) = 0,8072 ⇔ 1,011 x – 4,048 + 1,012 x = 0,8072 ⇔ 2,023. x = 4,8552 ⇔ x = 2,4 ( thỏa mãn nhu cầu ) . Vậy dân số của tỉnh A là 2,4 triệu người, dân số tỉnh B là 4 – 2,4 = 1,6 triệu người

Bài 7: Giải bài toán bằng cách lập phương trình (tiếp)

Luyện tập (trang 31-32 sgk Toán 8 Tập 2)

Bài 49 (trang 32 SGK Toán 8 tập 2): Đố: Lan có một miếng bìa hình tam giác ABC vuông tại A, cạnh AB = 3cm. Lan tính rằng nếu cắt từu miếng bìa đó ra một hình chữ nhật có chiều dài 2cm như hình 5 thì hình chữ nhật ấy có diện tích bằng một nửa diện tích của miếng bìa ban đầu. Tính độ dài cạnh AC của tam giác ABC.

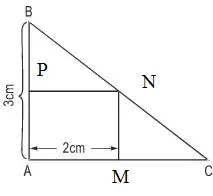
Lời giải:

Gọi x ( cm ) là cạnh AC ( x > 0 ) .
Gọi hình chữ nhật là MNPA thì MC = x – 2 ( cm )

Vì MN // AB nên ta có tỉ lệ:

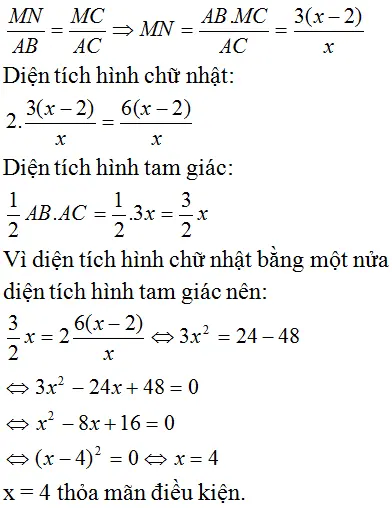
Vậy AC = 4cm.

Source: http://wp.ftn61.com
Category: Hỏi Đáp