Tóm tắt nội dung bài viết
Cách xác định nhanh góc giữa hai đường thẳng chéo nhau – Công thức và bài tập có đáp án
1. Định nghĩa góc giữa hai đường thẳng
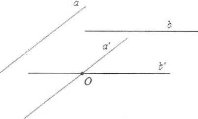
Trong khoảng trống cho 2 đường thẳng a, b bất kể .
Từ một điểm O nào đó ta vẽ 2 đường thẳng USD { a } ‘ USD, USD { b } ‘ USD lần lượt song song với a và b. Ta nhận thấy rằng khi điểm O đổi khác thì góc giữa 2 đường thẳng USD { a } ‘ USD và USD { b } ‘ USD không đổi khác .
Do đó ta có định nghĩa :
Định nghĩa: Góc giữa 2 đường thẳng a và b trong không gian là góc giữa 2 đường thẳng ${a}’$ và ${b}’$ cùng đi qua một điểm và lần lượt song song với a và b.
Bạn đang đọc: Cách xác định nhanh góc giữa hai đường thẳng chéo nhau – Công thức và bài tập có đáp án chi tiết
2. Cách xác định góc giữa hai đường thẳng
Để xác lập góc giữa 2 đường thẳng a và b ta hoàn toàn có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại .
Nếu USD \ overrightarrow { u } USD là vecto chỉ phương của đường thẳng a và USD \ overrightarrow { v } USD là vecto chỉ phương của đường thẳng b và USD \ left ( \ overrightarrow { u } ; \ overrightarrow { v } \ right ) = \ alpha USD thì góc giữa 2 đường thẳng a và b bằng USD \ alpha USD nếu USD 0 \ le \ alpha \ le 90 { } ^ \ circ USD và bằng USD 180 { } ^ \ circ – \ alpha USD nếu USD 90 { } ^ \ circ < \ alpha \ le 180 { } ^ \ circ USD. Nếu 2 đường thẳng a và b song song hoặc trùng nhau thì góc giữa chúng bằng USD 0 { } ^ \ circ USD. Góc giữa 2 đường thẳng là góc có số đo USD 0 \ le \ alpha \ le 90 { } ^ \ circ USD .
3. Phương pháp tính góc giữa hai đường thẳng
Để tính góc giữa hai đường thẳng trong khoảng trống tất cả chúng ta cần nhớ những công thức sau :
■ Định lý hàm số cosin trong tam giác ABC : USD \ cos \ widehat { BAC } = \ frac { A { { B } ^ { 2 } } + A { { C } ^ { 2 } } – B { { C } ^ { 2 } } } { 2. AB.AC } USD
Tương tự ta có : USD \ cos \ widehat { ABC } = \ frac { B { { A } ^ { 2 } } + B { { C } ^ { 2 } } – A { { C } ^ { 2 } } } { 2. BA.BC } USD và USD \ cos \ widehat { Ngân Hàng Á Châu } = \ frac { C { { A } ^ { 2 } } + C { { B } ^ { 2 } } – A { { B } ^ { 2 } } } { 2. CA.CB } USD
Chú ý: $\overrightarrow{AB}.\overrightarrow{AC}=AB.AC\cos \widehat{BAC}=\frac{1}{2}\left( A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}} \right)$
■ Tính góc giữa hai đường thẳng AB và CD ta tính góc giữa hai vectơ USD \ overrightarrow { AB } USD và USD \ overrightarrow { CD } USD dựa vào công thức USD \ cos \ left ( \ overrightarrow { AB } ; \ overrightarrow { CD } \ right ) = \ frac { \ overrightarrow { AB }. \ overrightarrow { CD } } { \ left | \ overrightarrow { AB } \ right |. \ left | \ overrightarrow { CD } \ right | } \ Rightarrow \ cos \ left ( AB ; CD \ right ) = \ frac { \ left | \ overrightarrow { AB }. \ overrightarrow { CD } \ right | } { \ left | \ overrightarrow { AB } \ right |. \ left | \ overrightarrow { CD } \ right | } USD từ đó suy ra góc giữa hai đường thẳng AB và CD .
Bài tập tính góc giữa hai đường thẳng d1 và d2 bằng có đáp án chi tiết
Bài tập 1: Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, $SA\bot \left( ABC \right)$ và $SA=a\sqrt{3}$. Gọi M, N lần lượt là trung điểm của AB và SC. Tính cosin góc giữa hai đường thẳng AN và CM.
Lời giải chi tiết
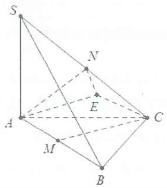
Cách 1: Dựng hình bình hành AMCE suy ra $AM=CE=\frac{a}{2}$.
Khi đó USD AE / / CM \ Rightarrow \ left ( \ widehat { AE ; CM } \ right ) = \ left ( \ widehat { AN ; AE } \ right ) = \ varphi. USD
Mặt khác USD SC = \ sqrt { S { { A } ^ { 2 } } + A { { C } ^ { 2 } } } = 2 a \ Rightarrow USD độ dài đường trung tuyến AN là USD AN = \ frac { SC } { 2 } = a. AE = CM = \ frac { a \ sqrt { 3 } } { 2 }. USD
Do USD \ Delta ABC USD đều nên USD CM \ bot AM \ Rightarrow USD AMCE là hình chữ nhật .
Khi đó USD CE \ bot AE USD mà USD CE \ bot SA \ Rightarrow CE \ bot \ left ( SAE \ right ) \ Rightarrow CE \ bot SE. USD
USD \ Delta SEC USD vuông tại E có đường trung tuyến USD EN = \ frac { 1 } { 2 } SC = a. USD
Ta có : USD \ cos \ widehat { NAE } = \ frac { A { { N } ^ { 2 } } + A { { E } ^ { 2 } } – N { { E } ^ { 2 } } } { 2. AN.AE } = \ frac { \ sqrt { 3 } } { 4 } > 0 \ Rightarrow \ cos \ varphi = \ frac { \ sqrt { 3 } } { 4 }. USD
Cách 2: Ta có: $\overrightarrow{AN}=\frac{1}{2}\left( \overrightarrow{AS}+\overrightarrow{AC} \right);\overrightarrow{CM}=\overrightarrow{AM}-\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}.$
Khi đó USD \ overrightarrow { AN }. \ overrightarrow { CM } = \ frac { 1 } { 2 } \ left ( \ overrightarrow { AS } + \ overrightarrow { AC } \ right ) \ left ( \ frac { 1 } { 2 } \ overrightarrow { AB } – \ overrightarrow { AC } \ right ) = \ frac { 1 } { 4 } \ overrightarrow { AB }. \ overrightarrow { AC } – \ frac { 1 } { 2 } A { { C } ^ { 2 } } = \ frac { 1 } { 4 } { { a } ^ { 2 } } \ cos 60 { } ^ \ circ – \ frac { { { a } ^ { 2 } } } { 2 } = \ frac { – 3 { { a } ^ { 2 } } } { 8 }. USD
Lại có : USD AN = \ frac { SC } { 2 } = a ; CM = \ frac { a \ sqrt { 3 } } { 2 } \ Rightarrow \ cos \ varphi = \ frac { \ left | \ frac { – 3 { { a } ^ { 2 } } } { 8 } \ right | } { a. \ frac { a \ sqrt { 3 } } { 2 } } = \ frac { \ sqrt { 3 } } { 4 }. USD
Bình luận: Dựa vào hai cách làm trên ta thấy rằng, trong một số trường hợp, việc sử dụng công cụ vectơ để tính góc giữa hai đường thẳng giúp bài toán trở nên dễ ràng hơn rất nhiều!.
Bài tập 2: Cho hình chóp S.ABC có $SA=SB=SC=AB=a;AC=a\sqrt{2}$ và $BC=a\sqrt{3}$. Tính cosin góc giữa hai đường thẳng SC và AB.
Lời giải chi tiết
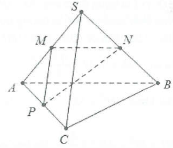
Cách 1: Gọi M, N, P lần lượt là trung điểm của SA, SB và AC. Khi đó $\left\{ \begin{array} {} MP//SC \\ {} N//AB \\ \end{array} \right.\Rightarrow \left( \widehat{SC;AB} \right)=\left( \widehat{MP;MN} \right).$
Ta có : USD MN = \ frac { AB } { 2 } = \ frac { a } { 2 } ; MP = \ frac { SC } { 2 } = \ frac { a } { 2 }. USD
Mặt khác USD \ Delta SAC USD vuông tại S USD \ Rightarrow SP = \ frac { AC } { 2 } = \ frac { a \ sqrt { 2 } } { 2 }. USD
$B{{P}^{2}}=\frac{B{{A}^{2}}+B{{C}^{2}}}{2}-\frac{A{{C}^{2}}}{4}=\frac{3}{2}{{a}^{2}}\Rightarrow BP=\frac{a\sqrt{6}}{2}.$
Xem thêm: Bảng tính toán kiểm tra độ võng của dầm
Suy ra USD P. { { N } ^ { 2 } } = \ frac { P. { { S } ^ { 2 } } + P. { { B } ^ { 2 } } } { 2 } – \ frac { S { { B } ^ { 2 } } } { 4 } = \ frac { 3 { { a } ^ { 2 } } } { 4 } \ Rightarrow NP = \ frac { a \ sqrt { 3 } } { 2 }. USD
Khi đó USD \ cos \ widehat { NMP } = \ frac { M { { N } ^ { 2 } } + M { { P } ^ { 2 } } – N { { P } ^ { 2 } } } { 2. MN.MP } = – \ frac { 1 } { 2 } \ Rightarrow \ widehat { NMP } = 120 { } ^ \ circ \ Rightarrow \ varphi = \ left ( \ widehat { SC ; AB } \ right ) = 60 { } ^ \ circ. USD
Cách 2: Ta có: $\overrightarrow{AB}=\overrightarrow{SB}-\overrightarrow{SA}\Rightarrow \overrightarrow{AB}.\overrightarrow{SC}=\left( \overrightarrow{SB}-\overrightarrow{SA} \right).\overrightarrow{SC}=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SC}$
USD = \ frac { 1 } { 2 } \ left ( S { { B } ^ { 2 } } + S { { C } ^ { 2 } } – A { { C } ^ { 2 } } \ right ) – \ frac { 1 } { 2 } \ left ( S { { A } ^ { 2 } } + S { { C } ^ { 2 } } – A { { B } ^ { 2 } } \ right ) = – \ frac { { { a } ^ { 2 } } } { 2 }. USD
Suy ra USD \ cos \ left ( SC ; AB \ right ) = \ frac { \ left | \ frac { – { { a } ^ { 2 } } } { 2 } \ right | } { a. a } = \ frac { 1 } { 2 } \ Rightarrow \ left ( SC ; AB \ right ) = 60 { } ^ \ circ. USD
Bài tập 3: Cho tứ diện ABCD có $AB={{x}_{1}},CD={{x}_{2}};AC={{y}_{1}},BD={{y}_{2}},BC={{z}_{1}},AD={{z}_{2}}$. Tính góc giữa hai đường thẳng BC và AD.
Lời giải chi tiết
Ta có : USD \ overrightarrow { BC }. \ overrightarrow { DA } \ text { } = \ text { } \ overrightarrow { BC } \ left ( \ overrightarrow { DC } + \ overrightarrow { CD } \ right ) = \ overrightarrow { CB }. \ overrightarrow { CD } – \ overrightarrow { CB }. \ overrightarrow { CD } USD
USD = \ frac { 1 } { 2 } \ left ( C { { B } ^ { 2 } } + C { { D } ^ { 2 } } – B { { D } ^ { 2 } } \ right ) – \ frac { 1 } { 2 } \ left ( C { { B } ^ { 2 } } + C { { A } ^ { 2 } } – A { { B } ^ { 2 } } \ right ) = \ frac { 1 } { 2 } \ left ( A { { B } ^ { 2 } } + C { { D } ^ { 2 } } – B { { D } ^ { 2 } } – C { { A } ^ { 2 } } \ right ). USD
Khi đó USD \ cos \ left ( BC ; DA \ right ) = \ frac { \ left | \ overrightarrow { BC }. \ overrightarrow { DA } \ right | } { BC.DA } = \ frac { x_ { 1 } ^ { 2 } + x_ { 2 } ^ { 2 } + y_ { 1 } ^ { 2 } – y_ { 2 } ^ { 2 } } { 2 { { z } _ { 1 } } { { z } _ { 2 } } }. USD
Đặc biệt: Nếu $AB=CD=x;AC=BD=y$ và $BC=AD=z$ ta đặt $\left\{ \begin{array} {} \alpha =\left( \widehat{BC;AD} \right) \\ {} \beta =\left( \widehat{AB;CD} \right) \\ {} \gamma =\left( \widehat{AC;BD} \right) \\ \end{array} \right.$ thì ta có:
USD \ cos \ alpha = \ frac { { { x } ^ { 2 } } – { { y } ^ { 2 } } } { { { z } ^ { 2 } } } ; \ cos \ beta = \ frac { \ left | { { y } ^ { 2 } } – { { z } ^ { 2 } } \ right | } { { { x } ^ { 2 } } } ; \ cos \ gamma = \ frac { { { z } ^ { 2 } } – { { z } ^ { 2 } } } { { { y } ^ { 2 } } }. USD
Bài tập 4: Cho hình chóp S.ABCD có đáy là hình vuông ABCD cạnh 2a, $SA\bot \left( ABCD \right)$ và $SB=a\sqrt{5}$. Gọi M là trung điểm của AB và N là trung điểm của BC. Tính cosin góc giữa 2 đường thẳng SM và DN .
Lời giải chi tiết
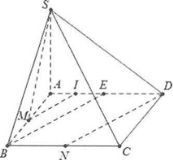
■ Cách 1: Do $SA\bot \left( ABCD \right).$
Ta có : $ SA = \ sqrt { S { { B } ^ { 2 } } – A { { B } ^ { 2 } } } = a USD. Gọi E là trung điểm của AD và I là trung điểm của AE. Dễ thấy BNDE là hình bình hành và MI là đường trung bình trong tam giác ABE. Khi đó USD Doanh Nghiệp / / BE / / MI. USD
Tacó : USD AM = a ; AI = \ frac { AE } { 2 } = \ frac { a } { 2 }. USD
Mặt khác : USD S { { M } ^ { 2 } } = S { { A } ^ { 2 } } + A { { M } ^ { 2 } } = 2 { { a } ^ { 2 } } ; S { { I } ^ { 2 } } = \ frac { 5 { { a } ^ { 2 } } } { 4 }. USD
USD MI = A { { I } ^ { 2 } } + A { { M } ^ { 2 } } = \ frac { 5 { { a } ^ { 2 } } } { 4 } USD. Do vậy USD \ cos \ widehat { SMI } = \ frac { S { { M } ^ { 2 } } + M { { I } ^ { 2 } } – S { { I } ^ { 2 } } } { 2. SM.MI } = \ frac { \ sqrt { 10 } } { 5 } = cos ( \ widehat { SM ; Doanh Nghiệp } ). USD
■ Cách 2: Ta có: $\overrightarrow{SM}.\overrightarrow{DN}\text{ }=\text{ }\overrightarrow{SM}.\left( \overrightarrow{SN}-\overrightarrow{SD} \right)=\overrightarrow{SM}.\overrightarrow{SN}\text{ }-\text{ }\overrightarrow{SM}.\overrightarrow{SD}$
USD \ text { = } \ frac { 1 } { 2 } \ left ( S { { M } ^ { 2 } } + S { { N } ^ { 2 } } – M { { N } ^ { 2 } } \ right ) – \ frac { 1 } { 2 } \ left ( S { { M } ^ { 2 } } + S { { D } ^ { 2 } } – M { { D } ^ { 2 } } \ right ) USD
Mặt khác : USD S { { N } ^ { 2 } } = S { { A } ^ { 2 } } + A { { N } ^ { 2 } } = S { { A } ^ { 2 } } + A { { B } ^ { 2 } } + B { { N } ^ { 2 } } = 6 { { a } ^ { 2 } }, MN = \ frac { AC } { 2 } = \ text { } a \ sqrt { 2 }, S { { D } ^ { 2 } } = 5 { { a } ^ { 2 } }, M { { D } ^ { 2 } } = 5 { { a } ^ { 2 } }. USD
Do đó USD \ overrightarrow { SM }. \ overrightarrow { Doanh Nghiệp } = 2 { { a } ^ { 2 } } \ Rightarrow \ cos \ left ( SM ; Doanh Nghiệp \ right ) = \ frac { \ left | 2 { { a } ^ { 2 } } \ right | } { SM.DN } = \ frac { 2 { { a } ^ { 2 } } } { a \ sqrt { 2 }. a \ sqrt { 5 } } = \ frac { \ sqrt { 10 } } { 5 }. USD
Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật có $AB=a;AD=a\sqrt{2},\text{ }SA\bot \left( ABCD \right)$ và $\text{SA=2a}\text{.}$
a ) Tính cosin góc giữa hai đường thẳng BC và SD .
b ) Gọi I là trung điểm của CD. Tính cosin góc giữa hai đường thẳng SB và AI .
Lời giải chi tiết
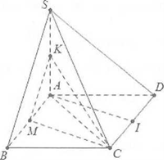
Xem thêm: Làm Thế Nào Để Active Windows 7
a ) Do USD BC / / AD \ Rightarrow ( \ widehat { SD ; BC } ) = ( \ widehat { SD ; AD } ) = \ widehat { SDA } USD
USD \ Delta SAD USD vuông tại A $ \ Rightarrow \ cos \ widehat { SDA } = \ frac { AD } { SD } = \ frac { AD } { \ sqrt { A { { D } ^ { 2 } } + S { { A } ^ { 2 } } } } = \ frac { 1 } { \ sqrt { 3 } }. USD
b ) Gọi M, K lần lượt là trung điểm của AB và SA thì MK là đường trung bình trong tam giác SAB .
Source: http://wp.ftn61.com
Category: Thủ Thuật



Để lại một bình luận