Bài 3. Phân tích hồi quy tuyến tính bội (Multiple Linear Regression)

1. Khi nào sử dụng?

Hồi quy tuyến tính bội là một phần lan rộng ra của hồi quy tuyến tính đơn. Nó được sử dụng khi tất cả chúng ta muốn Dự kiến giá trị của một biến phản hồi dựa trên giá trị của hai hoặc nhiều biến lý giải khác. Biến tất cả chúng ta muốn Dự kiến được gọi là biến phản hồi ( hoặc đôi lúc là biến phụ thuộc vào ). Các biến mà tất cả chúng ta đang sử dụng để Dự kiến giá trị của biến phản hồi được gọi là những biến lý giải ( hoặc đôi lúc là biến dự báo, biến nhờ vào ). Ví dụ, tất cả chúng ta hoàn toàn có thể sử dụng hồi quy bội số để hiểu liệu hoàn toàn có thể Dự kiến hiệu quả kỳ thi Toán lý giải dựa trên thời hạn ôn tập, và giới tính của sinh viên hay không .
Hồi quy bội cũng được cho phép tất cả chúng ta xác lập sự tương thích toàn diện và tổng thể của quy mô và góp phần tương đối của từng yếu tố dự báo vào tổng phương sai được lý giải. Ví dụ, tất cả chúng ta hoàn toàn có thể muốn biết mức độ biến hóa trong tác dụng kỳ thi cuối kì Toán lý giải hoàn toàn có thể được lý giải bằng thời hạn ôn tập và giới tính “ nói chung ”, nhưng cũng là “ góp phần tương đối ” của mỗi biến độc lập trong việc giải phương sai .

2. Giả thuyết vô hiệu và suy luận thống kê

Khi có nhiều hơn một biến độc lập, mô hình phù hợp tổng thể được đánh giá bằng thống kê F (F statistic). Giả thuyết vô hiệu được thử nghiệm liên quan đến tất cả các tham số hồi quy ngoại trừ điểm chặn. Ví dụ, nếu có ba biến giải thích trong mô hình thì giả thuyết vô hiệu sẽ là: H0: β1 = β2 = β3 = 0. Thống kê F được đánh giá là tỷ lệ giữa bình phương trung bình của mô hình so với bình phương trung bình của sai số.

3. Các giả định thống kê

Khi phân tích dữ liệu bằng cách sử dụng hồi quy tuyến tính, một phần của quy trình bao gồm việc kiểm tra để đảm bảo rằng dữ liệu muốn phân tích thực sự có thể được phân tích bằng hồi quy tuyến tính. Tập dữ liệu cần “vượt qua” các giả định cần thiết cho hồi quy tuyến tính để cung cấp kết quả hợp lệ.

• Việc đo lường biến phản hồi Y ít nhất phải liên tục về mặt lý thuyết. (Ví dụ: có thể sử dụng điểm trên thang đánh giá; 0, 1, 2, 3… n) và trong hồi quy bội, một hoặc nhiều biến giải thích có thể là nhị phân (ví dụ: trong hồi quy, chúng được gọi là biến giả – dummy variables, giới tính biến nhị phân có thể được mã hóa là 0 = nam, 1 = nữ) hoặc biến thứ tự.
• Mối quan hệ giữa các biến phản hồi và giải thích phải gần đúng tuyến tính. Xác minh bằng cách vẽ biểu đồ của biến phản hồi so với từng biến độc lập trong mô hình. Mối tương quan mạnh mẽ được biểu thị bằng xu hướng đường thẳng rõ ràng trong sự phân tán của các điểm.
• Sai số (error) trong mô hình hồi quy, ε, nên có phân phối xác suất chuẩn. Các phần dư (residuals) trong phân tích hồi quy đại diện cho các ước lượng mẫu của các sai số. Chúng phải có giá trị trung bình bằng 0 và phương sai không đổi (điều này được gọi là đồng nhất – homoscedasticity). Lưu ý rằng cả biến phản hồi hoặc biến giải thích đều không bắt buộc phải có phân phối chuẩn, chính các phần dư phù hợp mới là chuẩn.

– Xác minh giả định về tính chuẩn bằng cách thực thi vẽ biểu đồ Xác Suất chuẩn của những phần dư. Phân phối của phần dư chỉ cung ứng tín hiệu về sự phân bổ sai số cơ bản ( underlying error distribution ) trong dân số và hoàn toàn có thể không đáng an toàn và đáng tin cậy với những cỡ mẫu nhỏ. Cách diễn giải đồ thị Phần Trăm chuẩn theo cách tựa như như đã miêu tả trong bài ‘ Kiểm tra phân phối chuẩn ’ .
– Xác minh giả định về phương sai không đổi ( hoặc xác định sự như nhau ) bằng cách vẽ biểu đồ phần dư so với những giá trị Dự kiến. Sự phân tán ngẫu nhiên của những điểm về giá trị trung bình bằng 0 chỉ ra phương sai không đổi và thỏa mãn nhu cầu giả định này. Tức là những phương sai dọc theo đường tương thích nhất vẫn tương tự như khi bạn vận động và di chuyển dọc theo đường. Một quy mô hình phễu cho biết phương sai không hằng số. Những quan sát bên ngoài kì quặc hoàn toàn có thể thuận tiện phát hiện ra trên biểu đồ này .

• Không được có các điểm ngoại lệ đáng kể. Giá trị ngoại lệ là một điểm dữ liệu quan sát mà khiến giá trị biến phụ thuộc rất khác với giá trị được dự đoán bởi phương trình hồi quy. Để nhận điểm ngoại lệ (hoặc điểm dị biệt), xin vui lòng xem trong bài kiểm tra điểm ngoại lệ
• Dữ liệu không được xuất hiện đa cộng tuyến (multicollinearity), xảy ra khi có hai hoặc nhiều biến độc lập có tương quan cao với nhau. Điều này dẫn đến các vấn đề trong việc hiểu biến độc lập nào góp phần vào phương sai được giải thích trong biến phụ thuộc, cũng như các vấn đề kỹ thuật trong việc tính toán mô hình hồi quy bội số.

Tất cả các giả định đều quan trọng nhưng một số giả định còn hơn cả những giả định khác. Kinh nghiệm cho phép nhà nghiên cứu đánh giá xem các giả định có thể được nới lỏng đến mức nào trước khi các suy luận bị vô hiệu – đây cũng là một nghệ thuật giống như một môn khoa học. Ví dụ, việc thiếu tính chuẩn của các phần dư không phải là điều quan trọng, nhưng sai số chuẩn (standard errors) có thể bị thổi phồng. Tương tự, việc thiếu phương sai không đổi không có khả năng làm sai lệch nghiêm trọng các hệ số hồi quy nhưng các giá trị p liên quan sẽ cần được diễn giải một cách thận trọng. Vi phạm nghiêm trọng nhất là một sự ra đi đáng kể so với tuyến tính. Trong tình huống này, việc chuyển đổi dữ liệu hoặc một phương pháp phân tích thay thế nên được xem xét.

4. Phân tích hồi quy tuyến tính bội trong SPSS

Ví dụ, tất cả chúng ta hoàn toàn có thể sử dụng hồi quy tuyến tính để hiểu liệu tác dụng kỳ thi viết cuối kì của sinh viên hoàn toàn có thể được Dự kiến dựa trên thời hạn ôn tập cuối kì dành học môn Toán giải tích và yếu tố giới tính hay không. Có 20 sinh viên được mời tham gia một cuộc thử nghiệm, kể từ khi buổi học ở đầu cuối của môn Toán giải tích đến ngày thi cuối kì, họ được ý kiến đề nghị ghi lại tổng số giờ ôn bài ( cộng dồn của mỗi ngày ) dành cho môn Toán. Kết thúc kì thi, nhà điều tra và nghiên cứu tích lũy điểm số của 20 sinh viên này theo thang điểm 100, gán giá trị 1 = nữ, 2 = nam, và tổng hợp theo bảng dưới đây .

Các bước dưới đây hướng dẫn tất cả chúng ta cách phân tích hồi quy tuyến tính bội trong Thống kê SPSS .

– Bước 1: Click Analyze > Regression > Linear…

– Bước 2: Trong hộp thoại Linear Regression, chúng ta chuyển biến giải thích ‘giờ ôn tập‘ và ‘giới tính’ vào hộp Independent(s):, chuyến biến phản hồi ‘Diemthi‘ vào hộp Dependent(s):,

– Bước 3: Bây giờ chúng ta cần kiểm tra các giả định gồm: không có ngoại lệ đáng kể (điểm dị biệt), tính độc lập của các quan sát, tính đồng nhất, hiện tượng đa cộng tuyến và và phân phối chuẩn của sai số / phần dư. Chúng ta có thể thực hiện việc này bằng cách sử dụng các tính năng thống kê (Statistics) và biểu đồ (Plots), sau đó chọn các tùy chọn thích hợp trong hai hộp thoại này.

+ Trong nút Statistics, chúng ta nhấp chọn hộp Model fit cho độ phù hợp của mô hình, kiểm tra hiện tượng đa cộng tuyến Collinrearity diagnostics. Tại vùng Regression Coefficients, chúng ta nhấp mục ước lượng Estimates, khoảng tin cậy Confidence intervals (thường đặt ở 95%). Tại vùng Residuals, chúng ta nhấp chọn hộp Durbin-Watson về sự tương quan.

+ Để sử dụng kiểm định Durbin-Watson, thì phương trình hồi quy phải bao gồm hệ số chặn, do vậy, cần kiểm tra mục Inculde constant in equation ở nút Options.

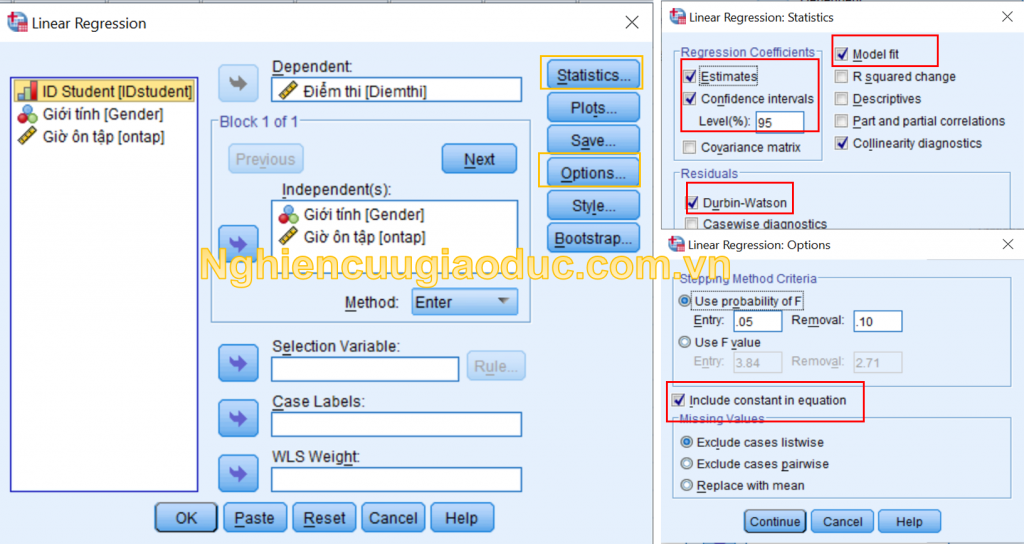
+ Trong nút Plots, chúng ta tiến hành vẽ đồ thị phần dư của ước lượng theo giá trị biến phải hồi để kiểm tra hiện tượng phương sai thay đổi và phân phối chuẩn của phần dư. Chúng ta chuyển mục *ZRESID vào hộp Y:, mục *ZPRED vào hộp X:. Sau đó nhấp chọn hộp Histogram, Normal Probability plot.

+ Sau mỗi bước thiết lập ở các nút, chúng ta click Continue để hoàn thành.

– Bước 4: Nhấp OK để chạy kết quả phân tích hồi quy.

Thống kê SPSS sẽ tạo ra khá nhiều bảng kết quả cho một hồi quy tuyến tính. Bảng quan tâm đầu tiên là bảng Model Summary.

Bảng này cung cấp các giá trị R và R2 (và R2 hiệu chỉnh), sai số của ước lượng và giá trị d của kiểm định Durbin-Watson. Giá trị R đại diện cho mối tương quan và trong ví dụ là R = 0.838, cho biết mức độ tương quan cao. Giá trị R2 (cột “R Square”) cho biết có bao nhiêu phần trăm trong tổng biến động trong các biến phản hồi, Diemthi, có thể được giải thích bằng các biến giải thích, Ontap, và gender. Trong trường hợp này, 70.2% có thể được giải thích, một con số rất lớn. Ngoài ra, giá trị thống kê d của kiểm định Durbin-Watson bằng 2.176 nằm trong khoảng 1.5 đến 2.5 thì cho thấy không có sự tương quan chuỗi (tự tương quan) bậc 1 giữa các phần dư. Trong trường hợp d nhỏ hơn 1.5 cho biết sự tương quan dương chuỗi bậc 1, và d lớn hơn 2.5 cho biết có sự tương quan âm chuỗi bậc 1.

Bảng tiếp theo là bảng ANOVA, báo cáo mức độ phù hợp của phương trình hồi quy với dữ liệu (tức là dự đoán biến phản hồi).

Bảng này chỉ ra rằng mô hình hồi quy dự đoán tốt biến phản hồi. Làm sao chúng ta biết được điều này? Nhìn vào hàng “Regression” và chuyển đến cột “Sig.“. Điều này cho thấy ý nghĩa thống kê của mô hình hồi quy đã được chạy. Ở đây, p <0.05, và chỉ ra rằng, về tổng thể, mô hình hồi quy dự đoán có ý nghĩa thống kê về các biến phản hồi (tức là nó phù hợp với dữ liệu).

Để khẳng định chắc chắn ý nghĩa thống kê cho sự phù hợp của mô hình hồi quy tổng thể, giá trị F thu được (F-test) được so sánh với giá trị F tới hạn (Critical F-value), xin vui lòng xem trong bảng giá trị tới hạn của phân phối F (F-distribution). Giá trị F tới hạn trong bảng phân phối F được xác định bằng sự giao cắt giữa cột V1 (df của tử số của F), và hàng V2 (df của mẫu số hoặc sai số của F).

V1 = số lượng tham số β trong quy mô hồi quy – 1 = 3-1 = 2
V2 = n – số lượng tham số β trong quy mô hồi quy = 20 – 3 = 17

Tra bảng phân phối F với mức ý nghĩa 5% tại cột 1 và hàng 18 thu được giá trị F tới hạn là 3.59.

Kết quả kiểm tra F trong bảng ANOVA là 20.022 > 3.59 cho thấy mô hình hồi quy tổng thể là có ý nghĩa thống kê, tức là biến giải thích “số giờ ôn tập” và “giới tính” là dự đoán đáng kể biến phản hồi “điểm thi cuối kì môn Toán giải thích của các sinh viên”.

Bảng Coefficients cung cấp cho chúng ta thông tin cần thiết để dự đoán ‘Điểm thi’ từ ‘Giới tính’ (X1) và ‘Giờ ôn tập’ (X2), cũng như xác định xem hai biến giải thích này có đóng góp đáng kể về mặt thống kê vào mô hình hay không (bằng cách xem cột “Sig.“). Hơn nữa, chúng ta có thể sử dụng các giá trị trong cột “B” trong cột “Standardized Coefficients“.

Trong bảng Coefficients, các hệ số của phương trình hồi quy tuyến tính đơn bao gồm 1 hằng số cắt là 42.5, và tham số β1 của ước lượng tham số giới tính là 7.942, và tham số β2 của ước lượng tham số giờ ôn tập là 3.235. Kết quả cho thấy cả hai hệ số này đều có ý nghĩa thống kê (p<0.05). Phương trình hồi quy là: Diemthi = 42.5 + 7.942 (gender) + 3.235 (ontap).

Mỗi thông số β cho biết mức tăng trung bình của điểm thi tương quan đến mức tăng 1 đơn vị chức năng trong một yếu tố lý giải ( biến lý giải ). Cụ thể, điểm thi cuối kì của sinh viên nam trung bình cao hơn sinh viên nữ là 7.942 điểm ( trên thang điểm 100 ). Hoặc tăng 1 giờ ôn tập ôn Toán lý giải có tương quan đến sự tăng điểm thi cuối kỳ là 3.235 điểm ( trên thang điểm 100 ) .

Khoảng tin cậy không bao gồm 0 và tất cả các giá trị đều dương, do đó, hợp lý khi kết luận rằng chúng ta tin tưởng 95% về việc tìm ra mối quan hệ thuận trong dân số giữa điểm thi cuối kì môn Toán giải thích với yếu tố giới tính và giờ ôn tập của các sinh viên. Cụ thể, chúng ta hy vọng điểm thi cuối kì Toán giải thích sẽ tăng lên với mỗi giờ ôn tập của sinh viên, mức tăng này có thể dao động từ 1.763 đến 4.707 với mức trung bình tăng đơn vị là 3.235, hoặc chúng ta kì vọng điểm thi cuối kì của sinh viên nam trung bình cao hơn sinh viên nữ là 7.942 điểm, có thể dao động từ 0.701 đến 15.183 điểm (mức dao động rất lớn). Điều này có thể là do cỡ mẫu nhỏ hoặc cần phải có các nghiên cứu giải thích hơn nữa.

Trong cột Collinearity Statistics, cột hệ số phóng đại phương sai VIF (variance inflation factor) < 2 cho thấy hiện tượng đa cộng tuyến bị loại bỏ. (Nếu hệ số phóng đại phương sai VIF (variance inflation factor) > 2 thì có dấu hiệu đa cộng tuyến, đây là điều không mong muốn. Nếu VIF > 10 thì chắc chắn có đa cộng tuyến). Chúng ta cũng có thể xem xét giá trị Tolerance bằng công thức Tolerance=1/VIF. Hệ số này nằm cột bên trái của hệ số VIF. Tương ứng là: nếu hệ số Tolerance bé hơn 0.5 thì có dấu hiệu đa cộng tuyến, đây là điều không mong muốn. Nếu giá trị Tolerance bé hơn 0.1 thì chắc chắn có đa cộng tuyến. Tuy nhiên, trong ví này hiện tượng đa cộng tuyến bị loại bỏ do các giá trị Tolerance > 0.5.

Bảng Collinearity Diagnostics cung cấp thống kê các giá trị liên quan đến hiện tượng đa cộng tuyến.

Bảng Residuals Statistics cung cấp thống kê các giá trị về phần dư với các mô tả về min, max, trung bình, độ lệch chuẩn. Trong ví dụ cho thấy giá trị trung bình của phần dư bằng 0 là đáp ứng giả định của phân tích hồi quy.

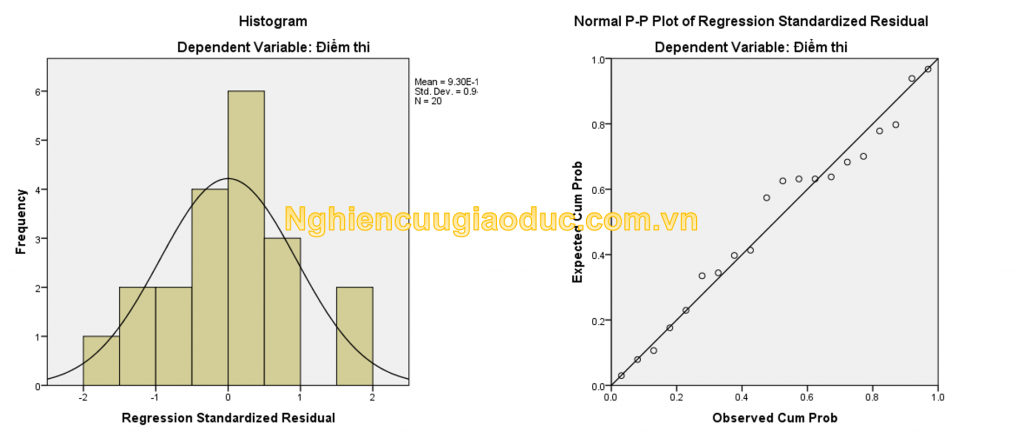
 Đồ thị phần dư chuẩn hóa hồi quy (Regression Standardized Residual) của biến phản hồi Y ‘Điểm thi’ cho biết phân phối của phần dư. Có thể thấy một vài thanh hơi cao và đâm xuyên qua đường cong chuẩn. Nhưng nói chung, mặc dù có một số sai lệch so với đường chuẩn nhưng không nhiều. Hầu hết các nhà phân tích sẽ kết luận rằng phần còn lại được phân phối gần như chuẩn (xấp xỉ/ gần đúng chuẩn). Ở đồ thị Normal P-P của phần dư chuẩn hóa hồi quy (Normal P-P Plot of Regression Standardized Residual) của biến phản hồi Y ‘Điểm thi’ cho thấy các giá trị quan sát phân phối xấp xỉ đường thẳng ứng với phân phối chuẩn. Kết quả này cho thấy phần dư có phân phối xấp xỉ chuẩn.

Ở đồ thị Scatter Plot của phần dư theo giá trị phản hồi (tức là mối quan hệ giữa Regression Standardized Residual với Regression Standardized Predicted value) thường được sử dụng để kiểm tra a) tính đồng nhất và b) các giả định về độ tuyến tính. Nếu cả hai giả định đều đúng, biểu đồ phân tán này sẽ không hiển thị bất kỳ đường mô hình mẫu nào.

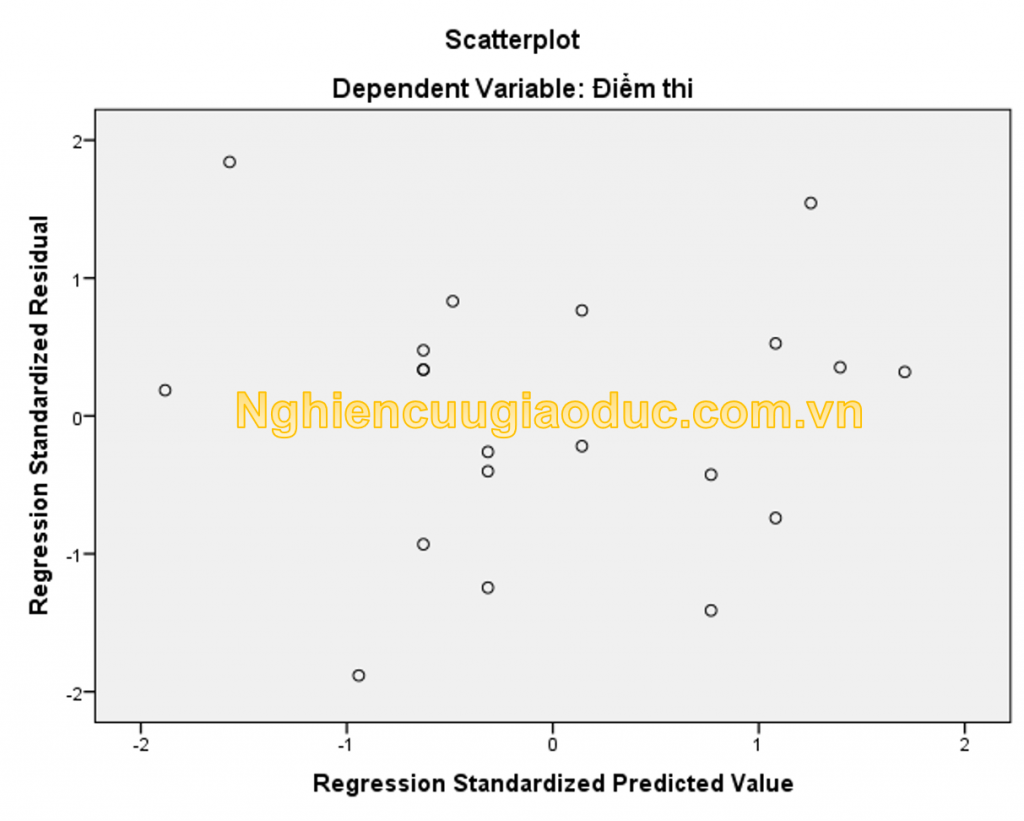
– Kiểm tra chung cho giả định về sự tuyến tính là kiểm tra xem các chấm trong biểu đồ phân tán này có hiển thị bất kỳ loại đường cong nào không. Đó không phải là trường hợp ở đây vì vậy sự tuyến tính dường như cũng được chấp nhận ở đây.

– Phương sai của phần dư là giống hệt chính do ước tính từ khoảng cách những chấm trong biểu đồ phân tán của tất cả chúng ta nằm cách nhau theo chiều dọc. Do đó, độ cao của biểu đồ phân tán của tất cả chúng ta không được tăng hoặc giảm khi tất cả chúng ta chuyển dời từ trái sang phải .

Tài liệu tham khảo

1. Coolican, H. (2018). Research methods and statistics in psychology. Routledge.
2. Hanneman, R. A., Kposowa, A. J., & Riddle, M. D. (2012). Basic statistics for social research (Vol. 38). John Wiley & Sons.
3. Jackson, S. L. (2015). Research methods and statistics: A critical thinking approach. Cengage Learning.
4. McQueen, R. A., & Knussen, C. (2006). Introduction to research methods and statistics in psychology. Pearson education.
5. Peers, I. (2006). Statistical analysis for education and psychology researchers: Tools for researchers in education and psychology. Routledge.
6. Wagner III, W. E. (2019). Using IBM® SPSS® statistics for research methods and social science statistics. Sage Publications.

Source: http://wp.ftn61.com
Category: Tin Tức