Bài 15,16 trang 45 Toán 9 tập 2: Công thức nghiệm của phương trình bậc hai

Đáp án và hướng dẫn Giải bài 15,16 trang 45 Toán 9 tập 2: Công thức nghiệm của phương trình bậc hai – Chương 4 phần Đại số.

Đối với phương trình ax2 + bx + c = 0 ( a ≠ 0 )
và biểu thức ∆ = b2 – 4 ac :

– Nếu ∆ > 0 thì phương trình có hai nghiệm phân biết:

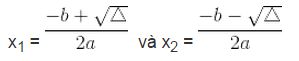
– Nếu ∆ = 0 thì phương trình có nghiệm kép

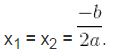
– Nếu ∆ < 0 thì phương trình vô nghiệm . Chú ý : Nếu phương trình ax2 + bx + c = 0 ( a ≠ 0 ) có a và c trái dấu, tức là ac < 0. Do đó ∆ = b2 – 4 ac > 0. Vì thế phương trình có hai nghiệm phân biệt .

Hướng dẫn giải bài tập công thức nghiệm của phương trình bậc hai Toán 9 tập 2 trang 45

Bài 15. Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức ∆ và xác định số nghiệm của mỗi phương trình sau:

a ) 7×2 – 2 x + 3 = 0 b ) 5×2 + 2 √ 10 x + 2 = 0 ;

d ) 1,7 x2 – 1,2 x – 2,1 = 0 .

Giải: a) 7×2 – 2x + 3 = 0 có a = 7, b = -2, c = 3

∆ = ( – 2 ) 2 – 4. 7. 3 = – 80 : Vô nghiệm
b ) 5×2 + 2 √ 10 x + 2 = 0
có a = 5, b = 2 √ 10, c = 2
∆ = ( 2 √ 10 ) 2 – 4. 5. 2 = 0 : nghiệm kép

d ) d ) 1,7 x2 – 1,2 x – 2,1 = 0 có a = 1,7 ; b = – 1,2 ; c = – 2,1
∆ = ( – 1,2 ) 2 – 4. 1,7. ( – 2,1 ) = 1,44 + 14,28 = 15,72 :

Phương trình có hai nghiệm phân biệt.

Bài 16. Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:

a ) 2×2 – 7 x + 3 = 0 ; b ) 6×2 + x + 5 = 0 ;
c ) 6×2 + x – 5 = 0 ; d ) 3×2 + 5 x + 2 = 0 ;
e ) y2 – 8 y + 16 = 0 ; f ) 16 z2 + 24 z + 9 = 0 .

Giải: a) 2×2 – 7x + 3 = 0 có a = 2, b = -7, c = 3

∆ = ( – 7 ) 2 – 4. 2. 3 = 49 – 24 = 25, √ ∆ = 5

b ) 6×2 + x + 5 = 0 có a = 6, b = 1, c = 5
∆ = 12 – 4. 6. 5 = – 119 < 0 : Phương trình vô nghiệm c ) 6x2 + x – 5 = 0 có a = 6, b = 5, c = - 5 ∆ = 12 – 4. 6. ( - 5 ) = 121, √ ∆ = 11

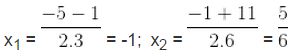
d ) 3×2 + 5 x + 2 = 0 có a = 3, b = 5, c = 2
∆ = 52 – 4. 3. 2 = 25 – 24 = 1, √ ∆ = 1

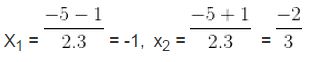
e) y2 – 8y + 16 = 0 có a = 1, b = -8, c = 16

∆ = ( – 8 ) 2 – 4. 1. 16 = 0

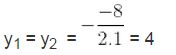
f ) 16 z2 + 24 z + 9 = 0 có a = 16, b = 24, c = 9
∆ = 242 – 4. 16. 9 = 0

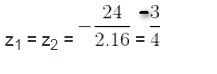
Source: http://wp.ftn61.com
Category: Hỏi Đáp