Cách giải và biện luận phương trình bậc nhất cực hay, chi tiết
Trang trước
Trang sau
Quảng cáo
Bạn đang đọc: phương trình ax+b=0 có bao nhiêu nghiệm
Cách giải và biện luận phương trình dạng ax + b = 0 được tóm tắt trong bảng sau
| ax + b = 0(1) | ||
| Hệ số | Kết luận | |
| a 0 | (1) có nghiệm duy nhất x = -b/a | |
| a = 0 | b 0 | (1) vô nghiệm |
| b = 0 | (1) nghiệm đúng với mọi x | |
Khi a 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn
Bài 1: Cho phương trình (m2 – 7m + 6)x + m2 – 1 = 0
a. Giải phương trình khi m = 0
b. Biện luận theo m số nghiệm của phương trình
Hướng dẫn:
a. Với m = 0 phương trình trở thành 6 x – 1 = 0 x = 1/6
Phương trình có nghiệm duy nhất x = 1/6
b. Ta có ( mét vuông – 7 m + 6 ) x + mét vuông – 1 = 0 ( m-1 ) ( m-6 ) x + ( m-1 ) ( m + 1 ) = 0
Nếu (m-1)(m-6) 0 thì phương trình có nghiệm duy nhất x = -(m+1)/(m-6)
Nếu m = 1 phương trình trở thành 0 = 0. Khi đó phương trình có vô số nghiệm .
Nếu m = 6 thì phương trình trở thành 35 = 0 ( Vô lí ). Khi đó phương trình vô nghiệm .
Quảng cáo
Bài 2: Tìm tất cả các giá trị thực của tham số m để phương trình (2m – 4)x = m – 2 có nghiệm duy nhất.
Hướng dẫn:
Phương trình đã cho có nghiệm duy nhất khi 2 m – 4 0 m 2
Bài 3: Tìm tất cả các giá trị thực của tham số m để phương trình (m2 – 5m + 6)x = m2 – 2m vô nghiệm.
Hướng dẫn:
Phương trình đã cho vô nghiệm khi
Bài 4: Tìm tất cả các giá trị thực của tham số m để phương trình (m2 – 1)x = m – 1 có nghiệm đúng với mọi x thuộc R.
Hướng dẫn:
Phương trình đã cho nghiệm đúng với x R hay phương trình có vô số nghiệm khi
Bài 5: Cho phương trình m2x + 6 = 4x + 3m. Tìm tất cả các giá trị thực của tham số m để phương trình đã cho có nghiệm.
Hướng dẫn:
Phương trình viết lại ( mét vuông – 4 ) x = 3 m – 6 .
Phương trình đã cho vô nghiệm khi
Do đó, phương trình đã cho có nghiệm khi m – 2
Bài 6: Cho hai hàm số y = (m + 1)2x – 2 và y = (3m + 7)x + m. Tìm tất cả các giá trị của tham số m để đồ thị hai hàm số đã cho cắt nhau.
Hướng dẫn:
Đồ thị hai hàm số cắt nhau khi và chỉ khi phương trình
( m + 1 ) 2 x – 2 = ( 3 m + 7 ) x + m có nghiệm duy nhất
( mét vuông – m – 6 ) x = 2 + m có nghiệm duy nhất
Quảng cáo
Bài 7: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 10] để phương trình (m2 – 9)x = 3m(m – 3) có nghiệm duy nhất ?
Hướng dẫn:
Phương trình đã cho có nghiệm duy nhất khi m2-9 0 m ± 3
Vì m Z, m [ – 10 ; 10 ] nên
m { – 10 ; – 9 ; – 8 ; … ; – 4 ; – 2 ; – 1 ; 0 ; 1 ; 2 ; 4 ; … ; 10 }
Vậy 19 giá trị của tham số m thỏa mãn nhu cầu nhu yếu bài toán .
Chuyên đề Toán 10 : khá đầy đủ kim chỉ nan và những dạng bài tập có đáp án khác :
Giới thiệu kênh Youtube Tôi
Trang trước
Trang sau
Video liên quan
Source: http://wp.ftn61.com
Category: Hỏi Đáp
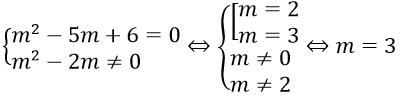
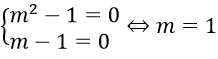
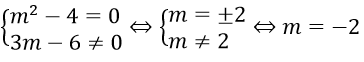
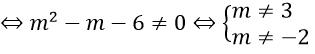



Để lại một bình luận