Phương trình đường thẳng trong không gian Oxyz – Toán học phổ thông

Viết phương trình đường thẳng trong không gian là chủ đề quan trọng trong chương trình toán học Trung học phổ thông. Để nắm chắc kiến thức về chuyên đề này, kiến thức lý thuyết cũng như các dạng toán và cách giải các loại bài tập, hãy cùng DINHNGHIA.VN tìm hiểu cụ thể qua bài viết dưới đây nhé!

Các dạng phương trình đường thẳng trong không gian

Bao gồm 2 dạng là phương trình chính tắc và phương trình tham số.

Đường thẳng d đi qua điểm \(M_{0}(x_{0},y_{0},z_{0})\) và có vec tơ chỉ phương \(\vec{u}=(a,b,c)\) có:

Phương trình tham số của đường thẳng d

\ ( \ left \ { \ begin { matrix } x = x_ { 0 } + at và \ \ y = y_ { 0 } + bt và \ \ z = z_ { 0 } + ct và \ end { matrix } \ right. \ )
Với \ ( t \ in R \ )

Phương trình chính tắc của đường thẳng d

\ ( \ frac { x-x_ { 0 } } { a } = \ frac { y-y_ { 0 } } { b } = \ frac { z-z_ { 0 } } { c } \ )
Với \ ( abc \ neq 0 \ )

Vị trí tương đối của hai đường thẳng

Vị trí tương đối của đường thẳng với mặt phẳng

Tìm hiểu về góc giữa hai đường thẳng

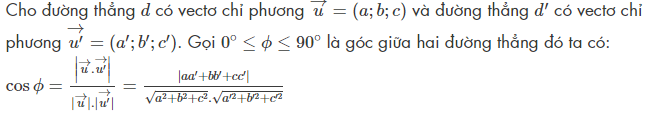
Tìm hiểu về góc giữa đường thẳng với mặt phẳng

Tìm hiểu khoảng cách giữa hai đường thẳng chéo nhau

Phương trình tổng quát đường thẳng trong không gian

Để viết được phương trình đường thẳng d ta quy d thành giao tuyến của mặt phẳng ( P ) và ( Q. ). Với
( P ) : \ ( A_ { 1 } x + B_ { 1 } y + C_ { 1 } z + D_ { 1 } = 0 \ )
( Q. ) : \ ( A_ { 2 } x + B_ { 2 } y + C_ { 2 } z + D_ { 2 } = 0 \ )
Thì phương trình tổng quát của d là :
\ ( \ left \ { \ begin { matrix } A_ { 1 } x + B_ { 1 } y + C_ { 1 } z + D_ { 1 } = 0 và \ \ A_ { 2 } x + B_ { 2 } y + C_ { 2 } z + D_ { 2 } = 0 và \ end { matrix } \ right. \ )
Khi đó vector chỉ phương của d là \ ( \ vec { u_ { d } } = \ left [ \ vec { n_ { P } }, \ vec { n_ { Q } } \ right ] \ )

Các dạng toán viết phương trình đường thẳng trong khoảng trống

Dạng 1 : Viết phương trình đường thẳng bằng cách xác lập vectơ chỉ phương

Dạng 2: Viết phương trình đường thẳng liên quan đến một đường thẳng khác

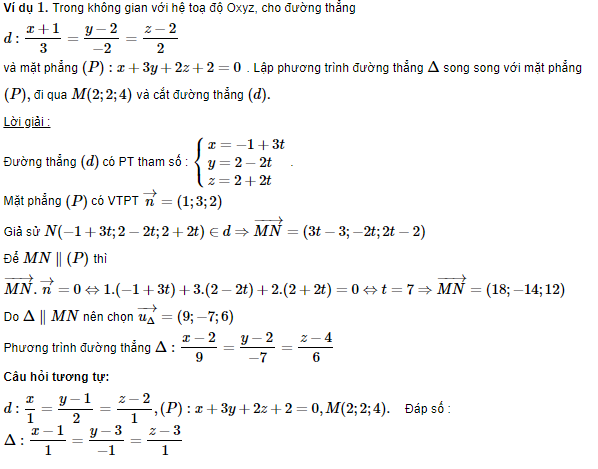
Dạng 3: Viết phương trình đường thẳng liên quan đến hai đường thẳng khác

Dạng 4: Viết phương trình đường thẳng liên quan đến khoảng cách

Phương trình đường thẳng Ox trong không gian

Đường thẳng Ox vuông góc với mặt phẳng Oyz nên nhận véc tơ ( 1,0,0 ) của trục Ox làm vector chỉ phương. Mặt khác Ox lại đi qua điểm O ( 0,0,0 ) nên phương trình đường thẳng Ox là : \ ( \ left \ { \ begin { matrix } x = t và \ \ y = 0 và \ \ z = 0 và \ end { matrix } \ right. \ )

Trên đây là bài viết tổng hợp kiến thức về phương trình đường thẳng trong không gian Oxyz. Nếu có bất kì đóng góp hay thắc mắc các bạn để lại bình luận bên dưới để cùng DINHNGHIA.VN trao đổi thêm nhé. Cảm ơn các bạn! Nếu thấy hay thì chia sẻ nha ^^

Xem thêm >>> Chuyên đề phương pháp tọa độ trong không gian: Lý thuyết và Bài tập

Xem thêm >>> Viết phương trình mặt phẳng trong không gian: Lý thuyết và Bài tập  
Xem chi tiết qua bài giảng sau:

(Nguồn: www.youtube.com)

5
/
5
(
2
bầu chọn

)

Please follow and like us :

Source: http://wp.ftn61.com
Category: Hỏi Đáp