








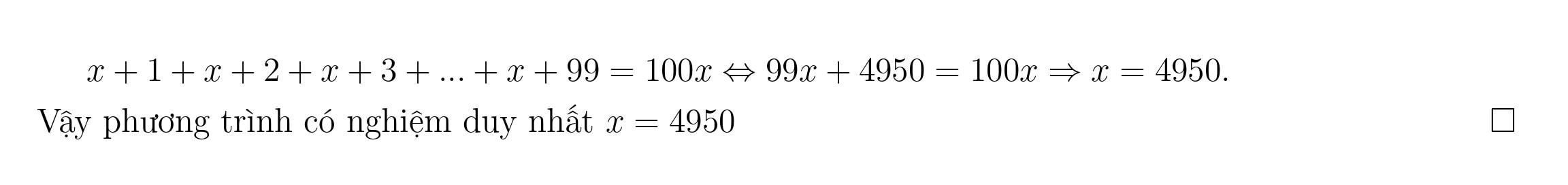
Nội dung bài viết Phương trình chứa ẩn trong dấu giá trị tuyệt đối:
Phương trình chứa ẩn trong dấu giá trị tuyệt đối. Nguyên tắc cơ bản trong giải phương trình chứa ẩn trong dấu giá trị tuyệt đối là phải tìm cách làm mất dấu giá trị tuyệt đối. Các phương pháp thường dùng là: Biến đổi tương đương, chia khoảng trên trục số. Phương pháp 1. Biến đổi tương đương. Với f(x), g(x) là các hàm số. Khi đó |f(x)| = g(x). Phương pháp 2. Chia khoảng trên trục số. Ta lập bảng xét dấu của các biểu thức trong dấu giá trị tuyệt đối rồi xét các trường hợp để khử dấu giá trị tuyệt đối. Một số cách khác. a) Đặt ẩn phụ. b) Sử dụng bất đẳng thức ta so sánh f(x) và g(x) từ đó tìm nghiệm của phương trình. c) Sử dụng đồ thị cần chú ý số nghiệm của phương trình f(x) = g(x) là số giao điểm của hai đồ thị hàm số y = f(x) và y = g(x). Phương pháp này thường áp dụng cho các bài toán biện luận nghiệm.
BÀI TẬP DẠNG 3. Phương pháp 1. Biến đổi tương đương. Ví dụ 1. Giải phương trình sau |2x − 3| = 5 − x. Vậy phương trình đã cho có hai nghiệm x = 8 và x = −2. Ví dụ 2. Giải phương trình |x − 2| = |3x + 2|. Vậy phương trình đã cho có hai nghiệm x = −2 và x = 0. BÀI TẬP TỰ LUYỆN. Bài 6. Giải và biện luận phương trình |x − 2m| = x + m. Kết luận: Với m 0 phương trình có nghiệm duy nhất x = 3m.
Phương pháp 2. Chia khoảng trên trục số. Ví dụ 4. Giải phương trình |x − 2| = 2x − 1. Ta xét hai trường hợp. TH1: Với x ≥ 2 phương trình trở thành x − 2 = 2x − 1 ⇒ x = −1 < 2 (loại). TH2: Với x < 2 phương trình trở thành −x + 2 = 2x − 1 ⇒ x = 1 < 2 (thỏa mãn). Vậy phương trình có nghiệm duy nhất x = 1. Ví dụ 5. Giải phương trình |x − 2| + |3x − 9| = |x + 1|. Lời giải. Lập bảng để khử dấu giá trị tuyệt đối. Khi đó ta xét từng trường hợp để khử dấu giá trị tuyệt đối như sau: TH1: Với x −1 ⇒ loại. TH2: Với −1 ≤ x < 2 phương trình trở thành −(x − 2) − (3x − 9) = x + 1 ⇔ x = 2 ⇒ loại. TH3: Với −2 ≤ x < 3 phương trình trở thành x − 2 − (3x − 9) = x + 1 ⇔ x = 2. TH4: Với x ≥ 3 phương trình trở thành x − 2 + 3x − 9 = x + 1 ⇔ x = 4. Vậy phương trình đã cho có hai nghiệm x = 2 và x = 4.
Ví dụ 6. Biện luận số nghiệm của phương trình |2x − 4m| = 3x + 2m. Lời giải. Ta sẽ xét từng trường hợp để loại bỏ dấu giá trị tuyệt đối TH1: Với x ≥ 2m thì phương trình trở thành 2x − 4m = 3x + 2m ⇒ x = −6m vì x ≥ 2m ⇒ −6m ≥ 2m ⇒ m ≤ 0. Vậy với m ≤ 0 thì phương trình có nghiệm x = −6m. TH2: Với x 0 thì phương trình có nghiệm x = 2m Kết luận: Với mọi m thì phương trình có một nghiệm. Bài 8. Giải phương trình |2x − 1| = |x + 2| + |x − 1|. Ta lập bảng để khử dấu giá trị tuyệt đối. Từ đó ta xét các trường hợp để bỏ dấu giá trị tuyệt đối. TH1: Với x < −2 phương trình trở thành −2x + 1 = −x − 2 − x + 1 ⇔ 0 = −3 ⇒ loại. TH2: Với −2 ≤ x < 1 phương trình trở thành −2x + 1 = x + 2 − x + 1 ⇔ x = −1. TH3: Với 1 ≤ x 1 ⇒ loại. TH4: Với x ≥ 1 phương trình trở thành 2x − 1 = x + 2 + x − 1 ⇔ −1 = 1 ⇒ loại. Vậy phương trình đã cho có một nghiệm x = −1.
Ví dụ 8. Biện luận số nghiệm của phương trình |x| + |x − 2| = m. Trước hết ta vẽ đồ thị hàm số y = |x| + |x − 2| lập bảng xét dấu. Từ đó vẽ đồ thị ứng với mỗi khoảng trong bảng xét dấu ta được đồ thị hình bên. Khi đó, số nghiệm của phương trình |x| + |x − 2| = m là số giao điểm của đồ thị hàm số y = |x| + |x − 2| và đường thẳng y = m. Dựa vào đồ thị ta thấy: Với m 2 thì phương trình luôn có hai nghiệm phân biệt. Ví dụ 9. Giải phương trình |x − 2016| + |x − 2017| = 1. Ta thấy x = 2016 hoặc x = 2017 là nghiệm của phương trình. TH1: Với x < 2016 ⇒ x − 2017 1 ⇒ |x − 2016| + |x − 2017| > 1 ⇒ phương trình không có nghiệm thỏa mãn x < 2016. TH2: Với 2016 < x < 2017 ⇒ phương trình không có nghiệm thỏa mãn 2016 < x < 2017.
Source: http://wp.ftn61.com
Category: Hỏi Đáp


Để lại một bình luận