[SGK Scan] ✅ Phương trình lượng giác cơ bản – Sách Giáo Khoa – Học Online Cùng http://wp.ftn61.com

Xem thêm các sách tham khảo liên quan:

Phương trình lượng giác cơ bản –
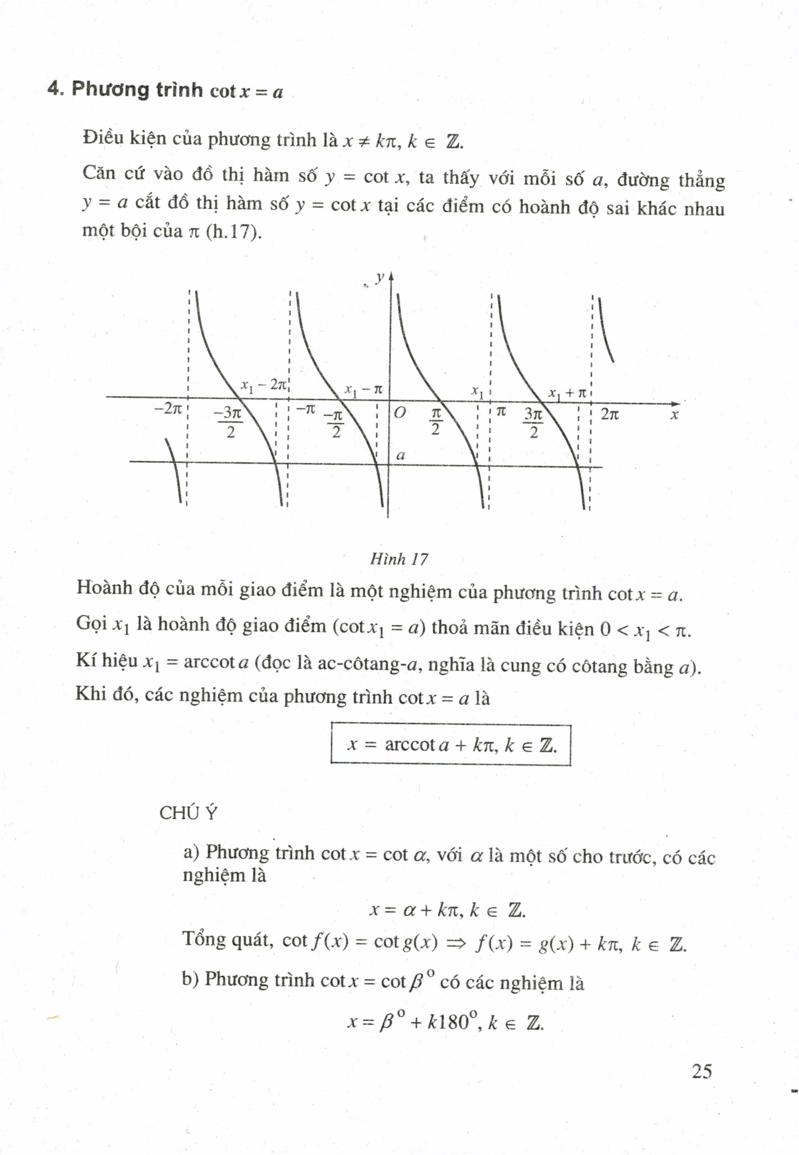
Trong trong thực tiễn, ta gặp những bài toán dẫn đến việc tìm tổng thể những giá trị của x nghiệm đúng những phương trình nào đó, như 3 sin 2 x + 2 = 0 hoặc 2 cos x + tan 2 x – l = 0, mà ta gọi là những phương trình lượng giác. Giải phương trình lượng giác là tìm tổng thể những giá trị của ẩn số thoả mãn phương trình đã cho. Các giá trị này là số đo của những cung ( góc ) tính bằng radian hoặc bằng độ. Việc giải những phương trình lượng giác thường đưa về việc giải những phương trình sau, gọi là những phương trình lượng giác cơ bản : sin x = a, cos x = a, tan v = a, cotx = a, trong đó a là một hằng số. 18 2 – ĐAI SỐ (, G | ẢI TÍCH 1 – o1. Phương trình sinx = a2 Có giá trị nào của x thoả mãn phương trình sinx = – 2 không ? Xét phương trình sin_x = a. ( 1 ) Trường hợp la | > 1 Phương trình ( 1 ) vô nghiệm, vì sinx | < 1 với mọi x. Trường hợp la | < 1V ẽ đường tròn lượng giác tâm O, trục hoành là trục côsin, trục tung là trục Sin. Trên trục sin lấy điểm K sao cho OK = a. Từ K kẻ đường vuông góc với trục sin, cắt đường tròn lượng giác tại M và M ' đối xứng với nhau qua trục sin ( nếu | a | = | thì M trùng với M " ) ( h. 14 ). A " / / ình 14 y Từ đó ta thấy số đo của những cung lượng giác AM và AM " là tổng thể những nghiệm của phương trình ( 1 ). - y مر Gọi C là số đo bằng radian của một cung lượng giác AM, ta có sd AM = oy + k27Li, k e = Z ; sd AM ' ' ' = TI - a + k2TT, k e Z. Vậy phương trình sinx = a có những nghiệm làΑ = α + K2π, k e Z ; x = л — ox + k. 2 л, k e = Z. - < a. s. .. .. - 2 2 thì ta Viết Cx = arcsin aNếu số thực và thoả mãn điều kiện kèm theo Sin Cx = a ( đọc là ac-sin-a, nghĩa là cung có Sin bằng a ). Khi đó, những nghiệm của phương trình sinx = a được viết là x = arcsin a + k2TT, k e Z và Y = ft – arcsin a + K27t, và = Z. 19 CHÚ Ý : a ) Phương trình sinx = sin C, với a là 1 số ít cho trước, có cácnghiệm làΑ = α + K2π, k e Z Và χ = π - α + K2π, k E Z. Tổng quát, f ( x ) = g ( x ) + k27t, k e Z f ( x ) = Tt — g ( x ) + k2Tt, k e Z. b ) Phương trình sinx = sin / 3 ” có những nghiệm là x = ( 3 ' + k360 ', k e Z và x = 180 ” – B ' + k360 ”, k. e. Z. c ) Trong một công thức về nghiệm của phương trình lượng giác không được dùng đồng thời hai đơn vị chức năng độ và radian. d ). Các trường hợp đặc biệt quan trọng : • a = 1 : Phương trình sinx = 1 có những nghiệm làsin f ( x ) = sin g ( x ) < => α = 5 + K2π, kε Ζ. 2 * a = – 1 ; Phương trình sinx = – 1 có những nghiệm là A = – + K2, kez. • a = 0 : Phương trình sinx = 0 có những nghiệm là x = kít, k e Z.Ví dụ 1. Giải những phương trình sau : а ) sin x = i ; b ) sin x = 1.5 Gidia ). Vì 1. sin ” nên Sin_ \ = 1. < > sin x = sin “ *. 2 6 2 6V ậy phương trình có những nghiệm làx = + k2ri, ke z và x = n – ; + k2n = o + k2r, ke Z.b ) Ta có sin \ = khi x = arcsin Vậy phương trình sinx – có những nghiệm làx = arcsin + k2rt, k e z và x = Fe – arcsin + k2rt, ke Z. 3. 汽 。 những phương trình sau : V2а ) b ) sin ( x + 45 ° = 一す 。 2. Phương trình cosx = a. Trường hợp a > 1 Phương trình cos \ = a vô nghiệm vì lcosx | < 1 với mọi x. Trường hợp la | < 1 Tương tự trường hợp phương trình sinx = a, ta lấy điểm H trên trục côsin sao cho OH = a. Từ H kẻ đường vuông góc với trục côsin, cắt đường tròn lượng giác tại M và M ' đối xứng với nhau qua trục côsin ( nếu | al = 1 thì M = M " ) ( h. 15 ). Hình 15T ừ đó ta thấy số đo của những cung lượng giác AM và AM " là toàn bộ những nghiệm của phương trình cos \ = a. Gọi a là Số đo bằng radian của một cung lượng giác ÁM, ta có : sd AM = a + k27t, ke Z ; sd AM = - a + k2t, ke Z. Vậy phương trình cosx = a có những nghiệm làχ = Eα + K2π. K E Z. 21 CHÚ Ý : a ) Phương trình cos \ = cos C, với Cx là 1 số ít cho trước, có những nghiệm là x = 土a + k2T 、 ke Z. Tổng quát, cos f ( x ) = cos g ( x ) f ( x ) = + g ( x ) + k2tt, ke Z. b ) Phương trình cosx = cos / ? ” có những nghiệm là x = + 6 ′ + k360 ”, k. e. Z. c ). Nếu số thực và thoả mãn những điều kiện kèm theo 0 < or < лEthì ta viết Cx = arccosa ( đọc là ac-cÔsin-a, có nghĩa là cung cócôsin bằng a ). Khi đó, những nghiệm của phương trình cosx = a còn được viết làx = + arccos a + k27t, k e Z.d ). Các trường hợp đặc biệt quan trọng : * a = 1 : Phương trình cosx = 1 có những nghiệm là X = k2π, k E Z. • a = − 1 : Phương trình cosx = - 1 có những nghiệm là α = π + K2π, k E Z. * a = 0 : Phương trình cosx = 0 có những nghiệm làx = + kit, kez. 2V í dụ 2. Giải những phương trình sau : a ) cosx = cos " b ) cos 3 x = _V2 6 2 c ) cosx = d ) cos ( x + 60 ' ) = Gidia ) coSv = cos ့ ် x = 士 ; + K2π. K E Z.b ). Vì v2. – cos nên 2 4. cos 3. x = – < > cos 3 x = cos ; < > 3 x = + + K2π. ; x = + “ ” + k2f, ke Z ج > 4. 3 c ) cos x = x = | accos + K2π, Κ Ε Ζ : V2d ). Vì = cos 45 ° nêncos ( x + 60 o ) = cos ( x + 60 ° ) = cos 45 ° < => x + 60 ° = + 45 ° + k360 ° x = – 15 ′ o –, ) κε Ζ ( “ ” “ | جيx = – 105 ′ + k360 ′ 4. Giải những phương trình sau : b ) cos x = 3 c ) cos ( x + 30 o ) = J31 a ) cos x = – ; 23. Phương trình tanx = aĐiều kiện của phương trình là Y Z s + Kπ ( k E Z ). Căn cứ vào đồ thị hàm số y = tanx, ta thấy với mỗi số a, đồ thị hàm số y = tanx cắt đường thẳng y = a tại những điểm có hoành độ sai khác nhau một bội của It ( h. 16 ). y3π. 흥 풍丁一n – 2 / – 2 n х ) — л O2 % / x1 + n 2 % 、 + 2 nHình 16H oành độ của mỗi giao điểm là một nghiệm của phương trình tan x = a. Gọix là hoành độ giao điểm ( tanx = a ) thoả mãn điều kiện kèm theo – < x < 5. Kí hiệu x = arctan a ( đọc là ac-tang-a, nghĩa là cung có tang bằng a ). Khi đó, nghiệm của phương trình tan_x = a làx = arctana + kt, kie Z.a ) Phương trình tan_x = tan o, với a là một số ít cho trước, có những nghiệm làCHÚ Ý : Α = α + Kπ, kε Ζ. Tổng quát, tan f ( x ) = tang ( x ) => f ( x ) = g ( x ) + kft, k e Z. b ) Phương trình tanx = tan / ? ” có những nghiệm là x = 6 ′ + k180 ”, k. e. Z Ví dụ 3. Giải những phương trình sau : a ) tanx = tan ; ; b ) tan 2 x = – c ) tan ( 3 x + 15 ″ ) = V3i. 1. 3 Giải a ) tanx = tant Wー л + kant, k e Z. 5 5 b ) tan 2 x = – x = – arctan – – + k -, k e Z. 2 3 2 c ) Vì N3 = tan 60 ° nên tan ( 3 x + 15 ° ) = N3 < > tan ( 3 x + 15 ° ) = tan 60 ° “ 3 x = 45 ” + k180 < > x = 15 ′ + kó0 ”, k. e. Z. I5 * những phương trình sau : a ) tan x = 1 ; b ) tanx = – 1 ; c ) tanx = 0.244. Phương trình cotx = aĐiều kiện của phương trình là x z kft, k e Z. Căn cứ vào đồ thị hàm số y = cotix, ta thấy với mỗi số a, đường thẳng y = a cắt đồ thị hàm số y = cotx tại những điểm có hoành độ sai khác nhau \ một bội của Tt ( h. 17 ). Hình 17 Hoành độ của mỗi giao điểm là một nghiệm của phương trình cotx = a. Gọi \ ! là hoành độ giao điểm ( cotxt = a ) thoả mãn điều kiện kèm theo 0 < x < 1. Kí hiệu x = arccota ( đọc là ac-côtang-a, nghĩa là cung có côtang bằng a ). Khi đó, những nghiệm của phương trình cot. x = a làCHÚ Ýa ) Phương trình cot \ = cot a, với a là một số ít cho trước, có cácnghiệm là Α = α + Kπ, k E Z.Tổng quát, cot f ( x ) = cot g ( x ) => f ( x ) = g ( x ) + kft, k = Z. b ) Phương trình cotx = cot / ? ” có những nghiệm là A = 6 ’ + k180 ”, k. e. Z. 25V í dụ 4. Giải những phương trình sau : a ) cot 4 x = cot 27 t7 b ) cot3 = – 2 : 1 c ) cot ( 2 x – 10 ″ ) = –. J3 Gidi27t 2 π. 7. a ) cot 4 x = cot – -> 4 x = – + k7 -> y = k k e Z.b ) cot 3. x = – 2 ke 3. x = arccot ( – 2 ) + kit X ニ arccot ( – 2 ) + ki, e Z.c ). Vì = cot 60 ° nênJ3 1 o cot ( 2 x – 10 ″ ) = – cot ( 2 x – 10 ′ ) = cot60 -> 2 x – 10 ′ = 60 ′ + k 180 ″ x = 35 ° + k90 ′, k = Z = 6 汽 。 những phương trình sau : a ) cotx = 1 ; b ) cotx = – 1 ; c ) cotx = 0. GHINHỞ Mỗi phương trình sin x = a ( la s 1 ) ; cos x = a ( la < 1 ) ; tan x = a ; cotx = a có vô số nghiệm. Giải những phương trình trên là tìm toàn bộ những nghiệm của chúng. B Ả I ĐQ C TH Ê MG | ẢI PHƯơNG TRìNH LƯợNG GIÁC CO BẢN | BẢNG MÁY TÍNH BỞ TÚ | Có thể sử dụng máy tính bỏ túi ( MTBT ) để giải những phương trình lượng giác cơ bản. Tuy nhiên, so với phương trình sin \ = a máy chỉ cho hiệu quả là arcsin a với đơn vị chức năng là radian hoặc đã được đổi ra độ. Lúc đó, theo công thức nghiệm ta viết Các nghiệm làx = arcsin a + k2TT, k e Z Và x = Tt — arcsin a + k2Tt, k e = Z. Tương tự, so với phương trình cosx = a máy chỉ cho tác dụng là arccosa, so với phương trình tan_x = a máy chỉ cho tác dụng là arctana. Ví dụ. Dùng MTBT CASIO fX – 500 MS, giải những phương trình sau : a ) sin x = 0,5 ; b ) cos x = - C ) tanx = v3. Giải a ). Nếu muốn có đáp số bằng độ thì bấm ba lần phím rồi bấm phím " 1 " để màn hình hiển thị hiện ra chữ D. Sau đó bấm liên tiếpiena E a B Dòng thứ nhất trên màn hình hiển thị hiện ra sin 0.5 ( có nghĩa là arcsin 0,5 ) và hiệu quả ở dòng thứ hai là 30 ° 0 ° 0 ( arcsin 0,5 đã được đổi ra độ ). Vậy phương trình sinx = 0,5 có những nghiệm làx = 30 ° + k360 °, ke Z Và x = 180 ՞ — 30 " + k360 ° = 150 " + k360 °, k = Z, b ) Bấm liên tiếpFt ( ) ( cos ) ( ( ) ) ( 1 ) ( GBR ) ( 3 ) G = GCDDòng thứ nhất trên màn hình hiển thị là cos " — ( 1 - 3 ) ( Có nghĩa là arccos ( và kết quảl 3. ở dòng thứ hai là 109 ° 28 ' 16.3 " ( arccos ( ) đã được đổi ra độ ). 27 1.2.3. Vậy phương trình cos \ -- có những nghiệm là Y s + 109 ° 28 ' 16 " + k360 °, ke Z.SHIFT C ) Bấm liên tép ■ @ 屬 @ o ) dòng thứ nhất trên màn hình hiển thị là tan " N3 ( có nghĩa là arctan \ 3 ) và tác dụng ở dòng thứ hai là 60 ° 0 ' 0 ( arctan \ 3 đã được đổi ra độ ). Vậy phương trình tan x = N3 có những nghiệm là x = 60 ° + { 180 °, k = Z. = CHU Y a ) Để giải phương trình sinx = 0,5 với hiệu quả là radian, ta bấm ba Moo lần phím rồi bấm phím @ shift Sau đó, bấm liên tục 鳕 ta được tác dụng gần đúng là 0,5236 ( arcsin 0,5 s 0.5236 ), Vậy phương trình sin_x = 0,5 có những nghiệm là χε 0,5236 + K2π, Κ, Ε. ΖVà x = r = 0,5236 + k2rt, keZ. b ) Để giải phương trình cotx = a bằng MTBT, ta đưa về giải phươngmàn hình hiện ra chữ R.trình tan_ \ = l Bời tộp Giải những phương trình sau : a ) sin ( x + 2 ) = 1 ; b ) sin 3 x = 1 ; c ) n -- 0 d ) sin ( 2 x + 20 ° ) = - Với những giá trị nào của Y thì giá trị của những hàm số y = sin3. x và y = sinx bằng nhau ? Giải những phương trình sau : b ) cos 3 x = cos 12 ” ; 2 - 1 ) = : a ) cos ( x - 1 ) 3.oo --- - d ) cos * 2 x = 28 Giải những phương trình sau : a ) sin 3 x — cos 5 x = 0 ; b ) tan 3 x tanx = 1 .

Source: http://wp.ftn61.com
Category: Hỏi Đáp