Điều Kiện Để Phương Trình Có 2 Nghiệm Thực, Khi Đó Delta Cần Thỏa Điều Kiện Gì

Khi những em học tới phương trình bậc 2 một ẩn, thì việc ghi nhớ cách tính biệt thức delta là điều tất yếu có vai trò chính để giải được phương trình bậc 2, cách tính biệt thức delta này những em đã ghi nhớ nằm lòng chưa ?

Bài viết này sẽ vấn đáp cho những em câu hỏi : Phương trình bậc 2 có nghiệm khi nào ? khi đó delta thỏa điều kiện kèm theo gì ? .

Đang xem: điều kiện để phương trình có 2 nghiệm thực

I. Phương trình bậc 2 – kiến thức cơ bản cần nhớ

• Xét phương trình bậc hai : ax2 + bx + c = 0 ( a ≠ 0 )
• Công thức nghiệm tính delta ( ký hiệu : Δ )
Δ = b2 – 4 ac
+ Nếu Δ > 0 : Phương trình có 2 nghiệm phân biệt :

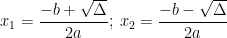
+ Nếu Δ = 0 : Phương trình có nghiệm kép :

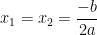
+ Nếu Δ 2 – ac với b = 2 b ” .
+ Nếu Δ ” > 0 : Phương trình có 2 nghiệm phân biệt :

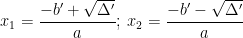
+ Nếu Δ ” = 0 : Phương trình có nghiệm kép :

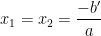
+ Nếu Δ” Phương trình bậc 2 có nghiệm khi nào?

– Trả lời: Phương trình bậc 2 có nghiệm khi biệt thức delta ≥ 0. (khi đó phương trình có nghiệm kép, hoặc có 2 nghiệm phân biệt).

> Lưu ý: Nếu cho phương trình ax2 + bx + c = 0 và hỏi phương trình có nghiệm khi nào? thì câu trả lời đúng phải là: a=0 và b≠0 hoặc a≠0 và Δ≥ 0.

• Thực tế so với bài toán giải phương trình bậc 2 thường thì ( không chứa tham số ), thì tất cả chúng ta chỉ cần tính biệt thức delta là hoàn toàn có thể đo lường và thống kê được nghiệm. Tuy nhiên bài viết này đề sẽ đề cập đến dạng toán hay làm những em hoảng sợ hơn, đó là tìm điều kiện kèm theo để phương trình bậc 2 có chứa tham số m có nghiệm .

II. Một số bài tập tìm điều kiện để phương trình bậc 2 có nghiệm

* Phương pháp giải:

– Xác định những thông số a, b, c của phương trình, đặc biệt quan trọng là thông số a. Phương trình ax2 + bx + c = 9 là phương trình bậc 2 chỉ khi a ≠ 0 .
– Tính biệt thức delta : Δ = b2 – 4 ac
– Xét dấu của biệt thức để Kết luận sự sống sót nghiệm, hoặc vận dụng công thức để viết nghiệm .

* Bài tập 1: Chứng minh rằng phương trình: 2×2 – (1 – 2a)x + a – 1 = 0 luôn có nghiệm với mọi giá trị của a.

* Lời giải:

– Xét phương trình : 2 × 2 – ( 1 – 2 a ) x + a – 1 = 0 có :
a = 2 ; b = – ( 1 – 2 a ) = 2 a – 1 ; c = a – 1 .
Δ = ( 2 a – 1 ) 2 – 4.2. ( a – 1 ) = 4 a2 – 12 a + 9 = ( 2 a – 3 ) 2 .
– Vì Δ ≥ 0 với mọi a nên phương trình đã cho luôn có nghiệm với mọi a .
Xem thêm : Diện Tích Xây Dựng Chung Cư Theo Tt Bxd Mới Nhất, Cách Xác Định Diện Tích Sàn Căn Hộ Chung Cư

* Bài tập 2: Cho phương trình mx2 – 2(m – 1)x + m – 3 = 0 (*). Tìm giá trị của m để phương trình trên có nghiệm.

* Lời giải:

– Nếu m = 0 thì phương trình đã cho trở thành : 2 x – 3 = 0 là phương trình bậc nhất một ẩn, có nghiệm x = 3/2 .
– Xét m ≠ 0. Khi đó phương trình đã cho là phương trình bậc 2 một ẩn, khi đó, ta có :
a = m ; b = – 2 ( m – 1 ) ; c = m – 3 .
Và Δ = 2 – 4. m. ( m-3 ) = 4 ( mét vuông – 2 m + 1 ) – ( 4 mét vuông – 12 m )
= 4 mét vuông – 8 m + 4 – 4 mét vuông + 12 m = 4 m + 4
– Như vậy, m = 0 thì pt ( * ) có nghiệm và với m ≠ 0 để phương trình ( * ) có nghiệm thì Δ ≥ 0 ⇔ 4 m + 4 ≥ 0 ⇔ m ≥ – 1 .
⇒ Kết luận : Phương trình ( * ) có nghiệm khi và chỉ khi m ≥ – 1 .

* Bài tập 3: Chứng minh rằng phương trình x2 – 2(m + 4)x + 2m + 6 = 0 luôn có nghiệm với mọi giá trị của m.

* Bài tập 4: Xác định m để các phương trình sau có nghiệm: x2 – mx – 1 = 0.

* Bài tập 5: Tìm giá trị của m để phương trình sau có nghiệm: 3×2 + (m – 2)x + 1 = 0.

* Bài tập 6: Tìm điều kiện của m để phương trình sau có nghiệm: x2 – 2mx – m + 1 = 0.

* Bài tập 7: Với giá trị nào của m thì phương trình sau: mx2 – 4(m – 1)x + 4m + 8 = 0 có nghiệm.

Xem thêm: Các Dạng Bài Tập Viết Phương Trình Tiếp Tuyến Chung Của 2 Đồ Thị Hàm Số

Như vậy với bài viết đã giải đáp được vướng mắc : Phương trình bậc 2 có nghiệm khi nào ? khi đó delta cần thỏa điều kiện kèm theo gì ? cùng những bài tập về tìm điều kiện kèm theo để phương trình bậc 2 có nghiệm ở trên đã giúp những em dễ hiểu hơn hay chưa ? Các em hãy cho góp ý và nhìn nhận ở dưới bài viết để tất cả chúng ta cùng trao đổi thêm nhé, chúc những em học tốt .

Xem thêm bài viết thuộc chuyên mục: Phương trình

Điều hướng bài viết

Source: http://wp.ftn61.com
Category: Hỏi Đáp