Phương trình đối xứng, phản đối xứng đối với sinx và cosx
A. Phương pháp giải
+ Phương trình đối xứng đối với sinx và cosx có dạng :
a (sinx+ cosx)+ b.sinx. cosx + c = 0
Để giải phương trình này ta làm như sau :
+ Phương trình phản đối xứng đối với sinx và cosx có dạng :
a ( sinx – cosx ) + b.sinx. cosx + c = 0
Để giải phương trình này ta làm như sau :

B. Ví dụ minh họa
Ví dụ 1: Phương trình sinx + cosx – 4.sinx.cosx – 1= 0 có bao nhiêu họ nghiệm
A. 2
B. 1
C. 3
D. 4
Lòi giải
Ta có : sinx + cosx – 4 sinx. cosx – 1 = 0
Chọn D .
Ví dụ 2: Giải phương trình sin2x – 12(sinx – cosx) + 12 = 0
A.
B.
C.
D. Tất cả sai
Lời giải
Đặt t = sinx – cosx = √ 2 sin ( x – π / 4 ) với | t | ≤ √ 2
⇒ sin2 x + cos2 x – 2sinx.cosx = t2
⇒ 1 – sin2x = t2 ⇒ sin2x = 1 – t2
Thay vào phương trình đã cho ta được : 1 – t2 – 12. t + 12 = 0
⇒ – t2 – 12 t + 13 = 0
Chọn C .
Ví dụ 3: Giải phương trình cos3 x + sin3 x= cos2 x- sin2x
A.
B.
C.
D. Đáp án khác
Lời giải
Ta có : cos3 x + sin3 x = cos2 x – sin2x
⇒ ( cosx + sinx ). ( cos2 x – cosx. sinx + sin2 x ) = ( cosx – sinx ). ( cosx + sinx )
⇒ ( cosx + sinx ). ( 1 – cos x. sinx ) – ( cosx – sinx ). ( cosx + sinx ) = 0
⇒ ( cosx + sinx ). ( 1 – cosx. sinx – cosx + sinx ) = 0
⇒ ( cosx + sinx ). [ ( 1 – cosx ) + ( sinx – cosx. sinx ) ] = 0
⇒ ( cosx + sinx ). [ ( 1 – cosx ) + sinx ( 1 – cos ) ] = 0
⇒ ( cosx + sinx ). ( 1 – cosx ). ( 1 + sinx ) = 0
Chọn C .
Ví dụ 4: Giải phương trình sin3 x – cosx + cos3 x- sinx = 2sin2x
A. x = kπ
B. x = kπ / 2
C. x = kπ / 4
D. Đáp án khác
Lời giải
Ta có : sin3 x – cosx + cos3 x – sinx = 2 sin2x
⇒ ( sin3 x + cos3 x ) – ( cosx + sinx ) – 2 sin2x = 0
⇒ ( sinx + cosx ). ( sin2 x – sinx.cosx + cos2 x ) – ( cosx + sinx ) – 2 sin2x = 0
⇒ ( sinx + cosx ). ( 1 – sinx. cosx ) – ( cosx + sinx ) – 2.2.sinx. cosx = 0
⇒ ( sinx + cosx ). ( 1 – sinx.cosx – 1 ) – 4.sinx. cosx = 0
⇒ – ( sinx + cosx ). sinx. cosx – 4.sinx.cosx = 0 ( * )
⇒ – sinx. cosx [ sinx + cosx + 4 ] = 0
Chọn B .
Ví dụ 5: Giải phương trình
A.
B.
C.
D. Đáp án khác
Lời giải
Đặt t = sinx-cosx = √ 2 sin ( x – π / 4 ) với | t | ≤ √ 2
⇒ sin2 x + cos2 x – 2 sinx. cosx = t2
⇒ 1 – 2 sinx. cosx = t2
⇒ 2sinx.cosx = 1 – t2
Chọn C .
Ví dụ 6. Giải phương trình
A.
B.
C.
D. Đáp án khác
Lời giải
+ Điều kiện : sinx ≠ 0
Chọn A .
Ví dụ 7. Phương trình: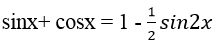
A.
B.
C.
D.
Lời giải
Đặt sinx + cosx = t ( | t | ≤ √ 2 )
⇒ sin 2 x + cos2 x + 2sinx.cosx = t2
⇒ 1 + sin2x = t2 ⇒ sin2x = t2 – 1
Thay vào phương trình đã cho ta được :
Chọn D .
Ví dụ 8. Phương trình 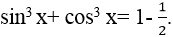
A.
B.
C.
D.Đáp án khác
Lời giải
Ta có : sin3 x + cos3 x = 1 – 50%. sin2x
⇒ ( sinx + cosx ). ( sin2 x – sinx. cosx + cos2 x ) = 1 – 50%. 2 sinx. cosx
⇒ ( sinx + cosx ). ( 1 – sinx. cosx ) = 1 – sinx. cosx
⇒ ( sinx + cosx ). ( 1 – sinx. cosx ) – ( 1 – sinx.cosx ) = 0
⇒ ( sinx + cosx – 1 ). ( 1 – sinx.cosx ) = 0
Chọn A .
Ví dụ 9. Giải phương trình |sinx-cosx|+4.sinx.cosx-1=0
A. x = kπ / 2
B. x = kπ
C. x = π / 2 + kπ
D. x = k2π
Lời giải
Đặt t = | sinx-cosx | = √ 2 | sin ( x – π / 4 ) | ( 0 ≤ t ≤ √ 2 )
⇒ sin2 x + cos2 x – 2 sinx. cosx = t2
⇒ 1 – 2 sinx. cosx = t2
⇒ 2 sinx. cosx = 1 – t2
Khi đó ; ta có : t + 2 ( 1 – t2 ) – 1 = 0
⇒ – 2 t2 + t + 1 = 0
C. Bài tập vận dụng
Câu 1:Tìm nghiệm dương bé nhất của phương trình :
A. x=
B. x=
C. x=
D. x=
Câu 2:Cho phương trình 5sin2x+sinx+cosx+6=0. Trong các phương trình sau, phương trình nào tương đương với phương trình đã cho?
A. sin x = 1/2
B. cosx = 1
C.cot x = 1
D. 1 + sin2x = 0
Câu 3:Câu 5.Giải phương trình: cos3 x+ sin3 x= cos2x
A.
B.
C.
D. Đáp án khác
Câu 4:Giải phương trình; sin(x+ π/4)+sin2x+1=0
A.
B.
C.
D.
Câu 5:Giải phương trình
A.
B.
C.
D.
Câu 6:Giải phương trình
A. x = + kπ
B.
C.
D.
Câu 7:Cho phương trình sinx.cosx – sinx- cosx + m= 0 trong đó m là tham số thực. Để phương trình có nghiệm, các giá trị thích hợp của m là
A. – √ 2-1 / 2 ≤ m ≤ 1
B. √ 2-1 / 2 ≤ m ≤ 1
C. – √ 2-1 / 2 < m < 1
D. Đáp án khác
Câu 8:Phương trình 2sin2x-3√6 |sinx+cosx|+8=0 có nghiệm là
A.
B.
C.
D. Đáp án khác
Câu 9:Giải phương trình sinx.cosx + 2(sinx+ cosx) = 2.
A.
B.
C.
D.
Source: http://wp.ftn61.com
Category: Hỏi Đáp
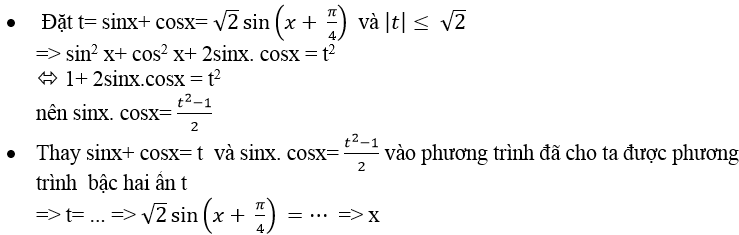
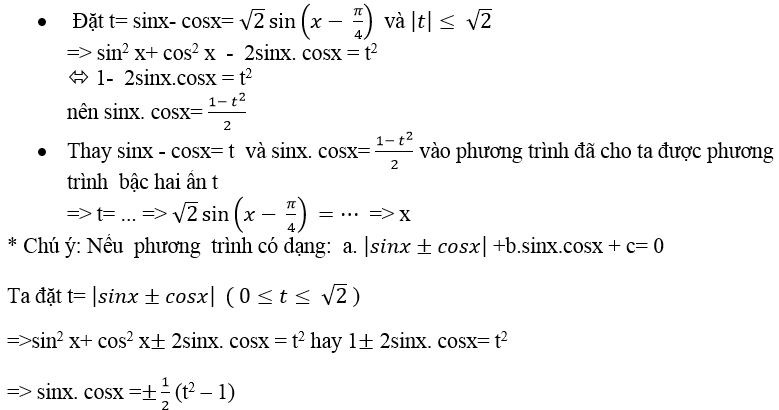
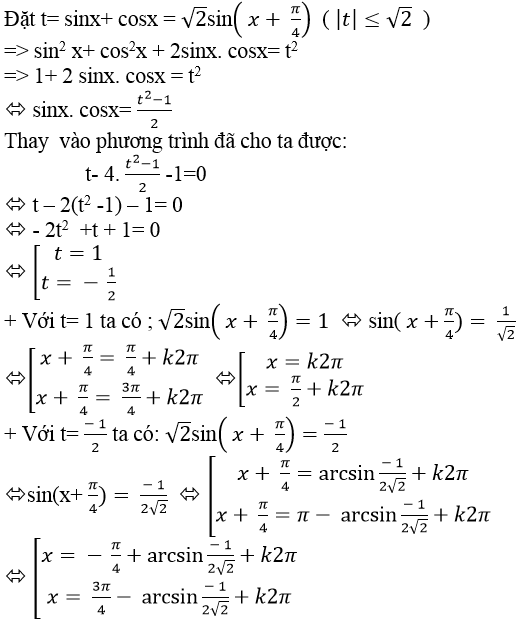
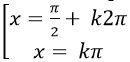
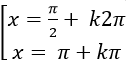
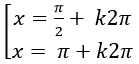
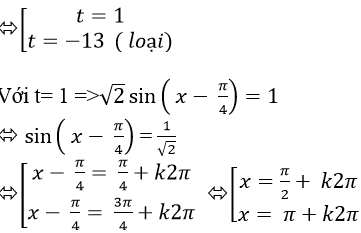
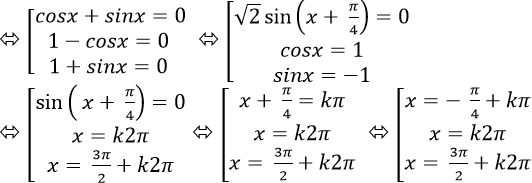
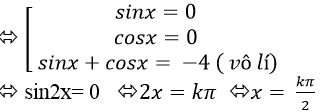
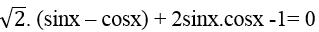
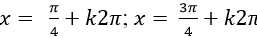

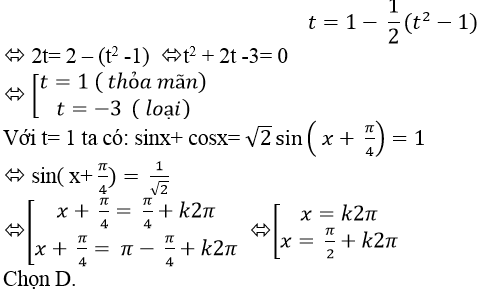
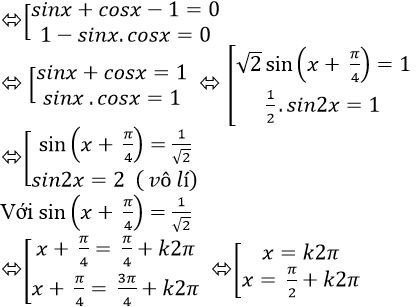



Để lại một bình luận