Bài viết phương trình đường thẳng trong không gian bao gồm: các dạng phương trình đường thẳng trong không gian, cách viết phương trình đường thẳng trong không gian, ví dụ bài tập viết phương trình đường thẳng trong không gian…
Tóm tắt nội dung bài viết
- Các dạng phương trình đường thẳng trong không gian
- Phương trình tham số
- Phương trình chính tắc
- Phương trình tổng quát đường thẳng trong không gian
- Phương trình đường thẳng Ox trong không gian
- Vị trí tương đối của hai đường thẳng
- Vị trí tương đối của đường thẳng với mặt phẳng
- Góc giữa hai đường thẳng
- Góc giữa đường thẳng với mặt phẳng
- Khoảng cách từ điểm đến đường thẳng có vectơ chỉ phương
- Khoảng cách giữa hai đường thẳng chéo nhau
- Ví dụ bài tập viết phương trình đường thẳng trong không gian
- Cách viết phương trình đường thẳng trong không gian
- Dạng I: Viết phương trình đường thẳng bằng cách xác định vectơ chỉ phương
- Dạng II: Viết phương trình đường thẳng liên quan đến một đường thẳng khác
- Dạng III: Viết phương trình đường thẳng liên quan đến hai đường thẳng khác
- Dạng IV: Viết phương trình đường thẳng liên quan đến khoảng cách
Các dạng phương trình đường thẳng trong không gian
Bao gồm 2 dạng là phương trình chính tắc và phương trình tham số .
Đường thẳng d đi qua điểm ![]()
và có vec tơ chỉ phương ![]() có:
có:
Phương trình tham số
và có vec tơ chỉ phươngcó :
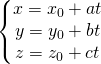
Với ![]()
Phương trình chính tắc
![]()
Với ![]()
Phương trình tổng quát đường thẳng trong không gian
Để viết được phương trình đường thẳng d ta quy d thành giao tuyến của mặt phẳng ( P ) và ( Q. ). Với
(P): ![]()
(Q): ![]()
Thì phương trình tổng quát của d là :
![]()
Khi đó vector chỉ phương của d là ![]()
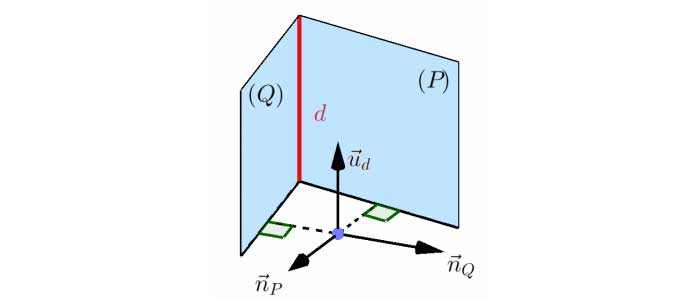
Phương trình đường thẳng Ox trong không gian
Đường thẳng Ox vuông góc với mặt phẳng Oyz nên nhận véc tơ (1,0,0) của trục Ox làm vector chỉ phương. Mặt khác Ox lại đi qua điểm O (0,0,0) nên phương trình đường thẳng Ox là: 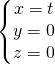
Vị trí tương đối của hai đường thẳng
Đường thẳng ![]() đi qua
đi qua ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() và đường thẳng
và đường thẳng ![]() đi qua
đi qua ![]() và có vectơ chỉ phương
và có vectơ chỉ phương ![]() . Khi đó:
. Khi đó:
+ và cùng nằm trong một mặt phẳng ![]() .
.
+ và cắt nhau ![Rendered by QuickLaTeX.com \Leftrightarrow\begin{cases}\left[ {\overrightarrow{u},\overrightarrow{u'}} \right].\overrightarrow{M_0M'_0}=0\\ \left[ {\overrightarrow{u},\overrightarrow{u'}} \right] \ne\overrightarrow{0} \end{cases}](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-e62d874f137819b47d8bb27fef818ca4_l3.png) .
.
+ ![Rendered by QuickLaTeX.com d \parallel d' \Leftrightarrow\begin{cases}\left[ {\overrightarrow{u},\overrightarrow{u'}} \right]=\overrightarrow{0}\\ \left[ {\overrightarrow{u},\overrightarrow{M_0M'_0}} \right] \ne\overrightarrow{0} \end{cases}](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-58826c6eb149f89ab1ee9221414b755e_l3.png) .
.
+ ![]()
+ và ![]() chéo nhau
chéo nhau ![]()
Vị trí tương đối của đường thẳng với mặt phẳng
Đường thẳng đi qua và có vectơ chỉ phương và mặt phẳng ![]() có vectơ pháp tuyến
có vectơ pháp tuyến ![]() . Khi đó:
. Khi đó:
+ cắt ![]()
+ 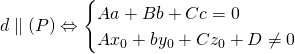
+ 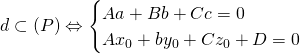
+ ![]()
Góc giữa hai đường thẳng
Cho đường thẳng có vectơ chỉ phương và đường thẳng có vectơ chỉ phương. Gọi ![]() là góc giữa hai đường thẳng đó ta có:
là góc giữa hai đường thẳng đó ta có:
![]()
Góc giữa đường thẳng với mặt phẳng
Cho đường thẳng có vectơ chỉ phương và mặt phẳng ![]() có vectơ pháp tuyến . Gọi
có vectơ pháp tuyến . Gọi ![]() là góc hợp bởi đường thẳng và mặt phẳng ta có:
là góc hợp bởi đường thẳng và mặt phẳng ta có:
![]()
Khoảng cách từ điểm 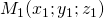 đến đường thẳng
đến đường thẳng 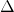 có vectơ chỉ phương
có vectơ chỉ phương 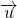
+ Cách ![]()
– Viết phương trình mặt phẳng ![]() qua
qua ![]() và vuông góc với .
và vuông góc với .
– Tìm tọa độ giao điểm ![]() của và mặt phẳng .
của và mặt phẳng .
– d![]() .
.
+ Cách ![]() Sử dụng công thức: d
Sử dụng công thức: d![]()
Khoảng cách giữa hai đường thẳng chéo nhau
Cho hai đường thẳng chéo nhau đi qua và có vectơ chỉ phương và đường thẳng ![]() đi qua và có vectơ chỉ phương
đi qua và có vectơ chỉ phương ![]() .
.
+ Cách
– Viết phương trình mặt phẳng chứa và song song với .
– Tính khoảng cách từ ![]() tới mặt phẳng .
tới mặt phẳng .
– d![]() d
d![]() .
.
+ Cách Sử dụng công thức: d![Rendered by QuickLaTeX.com (\Delta,\Delta')=\frac{\left| {\left[ {\overrightarrow{u},\overrightarrow{u'}} \right].\overrightarrow{M_0M'_0}} \right|}{\left| {\left[ {\overrightarrow{u},\overrightarrow{u'}} \right]} \right|}](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-93b19b84b67e2299535d5a7d2c5ea735_l3.png) .
.
Ví dụ bài tập viết phương trình đường thẳng trong không gian
Ví dụ 1. Viết phương trình đường thẳng d đi qua điểm ![]() và song song với giá của vectơ
và song song với giá của vectơ ![]() .
.
Giải
Vì d song song với giá của vectơ ![]() nên d nhận làm vectơ chỉ phương.
nên d nhận làm vectơ chỉ phương.
d đi qua điểm và có vectơ chỉ phương là nên có phương trình tham số :
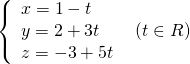
Ví dụ 2. Viết phương trình đường thẳng d đi qua hai điểm ![]() ,
, ![]() .
.
Giải
![]()
Vì d đi qua hai điểm M và N nên vectơ ![]() có giá trùng với d
có giá trùng với d ![]() là vectơ chỉ phương của d.
là vectơ chỉ phương của d.
d đi qua điểm và có vectơ chỉ phương là nên có phương trình tham số :
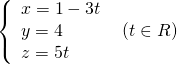
Ví dụ 3. Cho đường thẳng d có phương trình: ![]() . Tìm tọa độ điểm M thuộc d sao cho OM vuông góc với d (với O là góc tọa độ).
. Tìm tọa độ điểm M thuộc d sao cho OM vuông góc với d (với O là góc tọa độ).
Giải
Từ phương trình tham số của d, ta thấy d đi qua điểm ![]() và có VTCP là
và có VTCP là ![]() nên có phương trình tham số là:
nên có phương trình tham số là:
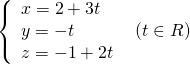
Vì ![]() .
.
![]()
Vì ![]()
![]()
![]()
Vậy ![]()
Cách viết phương trình đường thẳng trong không gian
Dạng I: Viết phương trình đường thẳng bằng cách xác định vectơ chỉ phương
Ví dụ ![]() Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
![]() và mặt phẳng
và mặt phẳng ![]() . Viết phương trình đường thẳng đi qua
. Viết phương trình đường thẳng đi qua ![]() , song song với mặt phẳng và vuông góc với đường thẳng
, song song với mặt phẳng và vuông góc với đường thẳng ![]()
Lời giải :
Để tìm một VTCP của ta phải tìm hai VTPT không cùng phương của nó rồi tìm tích có hướng của hai vectơ này.
Như vậy, ![]()
Trong đó ![]()
đi qua và có VTCP ![]() nên có phương trình
nên có phương trình
![]()
Ví dụ ![]() Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
![]() và mặt phẳng . Viết phương trình đường thẳng đi qua
và mặt phẳng . Viết phương trình đường thẳng đi qua ![]() , cắt và vuông góc với .
, cắt và vuông góc với .
Lời giải :
![]() . Gọi
. Gọi ![]() .
.
Do ![]() nên có thể giả sử
nên có thể giả sử ![]() .
.
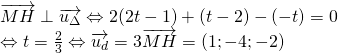
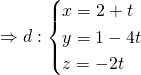
Dạng II: Viết phương trình đường thẳng liên quan đến một đường thẳng khác
Ví dụ Trong không gian với hệ toạ độ Oxyz, cho đường thẳng
![]()
và mặt phẳng ![]() . Lập phương trình đường thẳng song song với mặt phẳng
. Lập phương trình đường thẳng song song với mặt phẳng ![]() đi qua
đi qua ![]() và cắt đường thẳng
và cắt đường thẳng ![]()
Lời giải :
Đường thẳng ![]() có PT tham số :
có PT tham số : 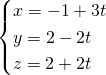 .
.
Mặt phẳng có VTPT ![]()
Giả sử ![]()
Để ![]() thì
thì 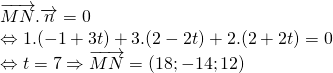
Do ![]() nên chọn
nên chọn ![]()
Phương trình đường thẳng ![]()
Dạng III: Viết phương trình đường thẳng liên quan đến hai đường thẳng khác
Ví dụ Trong không gian với hệ toạ độ Oxyz, viết phương trình đường thẳng đi qua điểm ![]() và cắt cả hai đường thẳng:
và cắt cả hai đường thẳng: 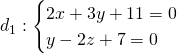 và
và ![]()
Lời giải :
Viết lại phương trình các đường thẳng: 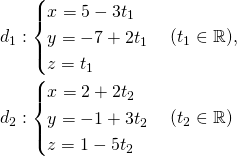
Gọi 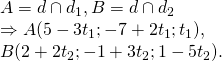
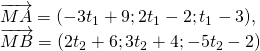
![Rendered by QuickLaTeX.com \left[ {\overrightarrow{MA},\overrightarrow{MB}} \right] = (-13t_1t_2 - 8t_1 +13t_2 +16;\\-13t_1t_2 + 39t_2;-13t_1t_2 - 24t_1 + 31t_2 + 48)](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-046323b79447a6423d85b6ede1d6987e_l3.png)
![]() thẳng hàng
thẳng hàng ![]() cùng phương
cùng phương ![]()
![]()
Đường thẳng qua ![]() và có VTCP
và có VTCP ![]()
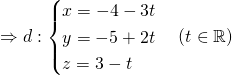
Dạng IV: Viết phương trình đường thẳng liên quan đến khoảng cách
Ví dụ Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 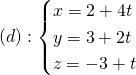 và mặt phẳng
và mặt phẳng ![]() . Viết phương trình đường thẳng
. Viết phương trình đường thẳng ![]() nằm trong song song với và cách một khoảng là
nằm trong song song với và cách một khoảng là ![]() .
.
Lời giải :
Chọn ![]() mà thấy rằng
mà thấy rằng ![]() nên
nên ![]()
Gọi là VTCP của ![]() , qua
, qua ![]() và vuông góc với thì
và vuông góc với thì 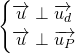
nên ta chọn ![]() .
.
Phương trình của đường thẳng 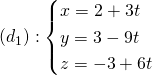
Lấy ![]() . là đường thẳng qua
. là đường thẳng qua ![]() và song song với
và song song với
Theo đề : ![]()
Với ![]()
Với ![]()
Ví dụ Trong không gian với hệ tọa độ Oxyz, cho đường thẳng 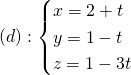 và mặt phẳng
và mặt phẳng ![]() . Gọi
. Gọi ![]() là giao điểm của và
là giao điểm của và ![]() Viết phương trình của đường thẳng nằm trong, vuông góc với sao cho khoảng cách từ đến bằng
Viết phương trình của đường thẳng nằm trong, vuông góc với sao cho khoảng cách từ đến bằng ![]() .
.
Lời giải :
có VTPT ![]() và có VTCP
và có VTCP ![]()
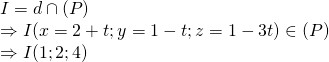
Vì ![]() có véc tơ chỉ phương
có véc tơ chỉ phương ![]()
Gọi là hình chiếu của trên ![]() qua và vuông góc
qua và vuông góc
![]() Phương trình
Phương trình ![]()
Gọi ![]() có VTCP
có VTCP ![]() và
và ![]() qua
qua 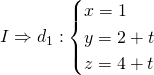
Giả sử ![]()
Ta có:
![]()
Với ![]()
Với ![]()
Sotayhoctap chúc các bạn học tốt!
5
/
5 ( 3 bầu chọn )
Source: http://wp.ftn61.com
Category: Hỏi Đáp



Để lại một bình luận