Tóm tắt nội dung bài viết
- Tóm tắt lý thuyết phương trình đường thẳng
- Vectơ pháp tuyến và phương trình tổng quát của đường thẳng
- Vectơ pháp tuyến của đường thẳng
- Phương trình tổng quát của đường thẳng Bạn đang đọc: #1 Toán 10: Phương Trình đường Thẳng đi Qua 2 điểm Trong Không Gian – Món Miền Trung
- Vectơ chỉ phương và phương trình tham số, phương trình chính tắc của đường thẳng
- Vectơ chỉ phương của đường thẳng
- Phương trình tham số của đường thẳng
- Phương trình chính tắc của đường thẳng
- Phương trình đường thẳng đi qua 2 điểm
- Khoảng cách từ 1 điểm tới 1 đường thẳng
- Vị trí tương đối của 2 đường thẳng
- Các dạng toán về phương trình đường thẳng
- Bài tập áp dụng phương trình đường thẳng
Tóm tắt lý thuyết phương trình đường thẳng
Vectơ pháp tuyến và phương trình tổng quát của đường thẳng
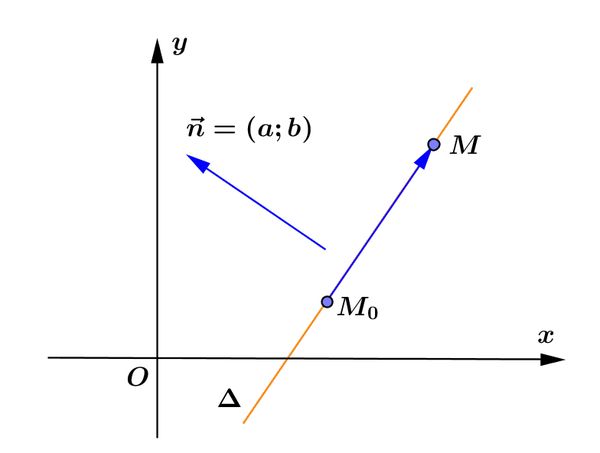
Vectơ pháp tuyến của đường thẳng
Vectơ n khác 0 và có giá vuông góc với đường thẳng được xem là vectơ pháp tuyến của đường thẳng. Khi đó, với k khác 0, vecto kn cũng là vectơ pháp tuyến của đường thẳng đó
Phương trình tổng quát của đường thẳng
Để viết phương trình tổng quát của đường thẳng d ta cần xác lập :
– Điểm A ( x0 ; y0 ) thuộc d
– Một vectơ pháp tuyến n ( a ; b ) của d
Khi đó phương trình tổng quát của d là : a ( x-x0 ) + b ( y-y0 ) = 0
* Cho đường thẳng d : ax + by + c = 0 nếu đường thẳng d / / ∆ thì đường thẳng ∆ có dạng : ax + by + c ’ = 0 ( c ’ ≠ c ) .
Vectơ chỉ phương và phương trình tham số, phương trình chính tắc của đường thẳng
Vectơ chỉ phương của đường thẳng
Vectơ a khác 0 và có giá song song hoặc trùng với đường thẳng được xem là vectơ chỉ phương của đường thẳng. Khi đó, với k khác 0 và vecto ka cũng là vectơ chỉ phương của đường thẳng đó .
Phương trình tham số của đường thẳng
Để viết phương trình tham số của đường thẳng ∆ ta cần xác lập
– Điểm A ( x0, y0 ) ∈ ∆
Để viết phương trình chính tắc của đường thẳng ∆ ta cần xác lập
– Điểm A ( x0, y0 ) ∈ ∆
( trường hợp ab = 0 thì đường thẳng không có phương trình chính tắc )
Chú ý :
– Nếu hai đường thẳng song song với nhau thì chúng có cùng VTCP và VTPT .
– Hai đường thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại
Hãy tìm hiểu thêm video sau đây để hiểu hơn về phương trình đường thẳng nhé !
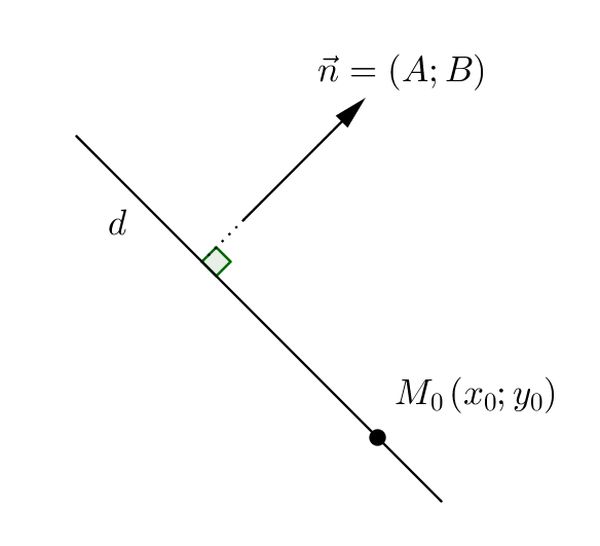
Phương trình chính tắc của đường thẳng
Trong mặt phẳng với hệ trục toạ độ vuông góc OxyOxy, cho đường thẳng dd
qua M0 ( x0 ; y0 ) và nhận
làm vectơ chỉ phương. Phương trình tham số của đường thẳng dd là
Trong trường hợp a và b đều khác 0 thì
ta có phương trình chính tắc của đường thẳng d là
Phương trình đường thẳng đi qua 2 điểm
Cách 1 :
Giả sử 2 điểm A và B cho trước có tọa độ là : A ( a1 ; a2 ) và B ( b1 ; b2 )
Gọi phương trình đường thẳng có dạng d : y = ax + b
Vì A và B thuộc phương trình đường thẳng d nên ta có hệ
Thay a và b ngược lại phương trình đường thẳng d sẽ được phương trình đường thẳng cần tìm .
Cách 2 giải nhanh
Tổng quát dạng bài viết phương trình đường thẳng đi qua 2 điểm : Viết phương trình đường thẳng đi qua 2 điểm A ( x1 ; y1 ) và B ( x2 ; y2 ) .
Cách giải :
Giả sử đường thẳng đi qua 2 điểm A ( x1 ; y1 ) và B ( x2 ; y2 ) có dạng : y = ax + b ( y * )
Vì ( y * ) đi qua điểm A ( x1 ; y1 ) nên ta có : y1 = ax1 + b ( 1 )
Vì ( y * ) đi qua điểm B ( x2 ; y2 ) nên ta có : y2 = ax2 + b ( 2 )
Từ ( 1 ) và ( 2 ) giải hệ ta tìm được a và b. Thay vào sẽ tìm được phương trình đường thẳng cần tìm .
Xem thêm : Công thức tính diện tích quy hoạnh, tính chu vi tam giác thường và những tam giác đặc biệt quan trọng đúng mực nhất
Xem thêm : Các giải pháp nghiên cứu và phân tích đa thức thành nhân tử và bài tập vận dụng
Khoảng cách từ 1 điểm tới 1 đường thẳng
Cho đường thẳng d: ax + by + c = 0 và điểm M ( x0; y0). Khi đó khoảng cách từ điểm M đến đường thẳng d là: d(M; d) =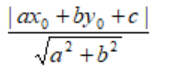 
+ Cho điểm A ( xA ; yA ) và điểm B ( xB ; yB ). Khoảng cách hai điểm này là :
AB = 
Chú ý : Trong trường hợp đường thẳng d chưa viết dưới dạng tổng quát thì tiên phong ta cần đưa đường thẳng d về dạng tổng quát .
Vị trí tương đối của 2 đường thẳng
Cho hai đường thẳng d1 : a1x + b1y + c1 = 0 và d2 : a2x + b2y + c2 = 0. Xét vị trí tương đối của hai đường thẳng d1 và d2 :
+ Cách 1 : Áp dụng trong trường hợp a1. b1. c1 ≠ 0 :
Cách 2: Dựa vào số điểm chung của hai đường thẳng trên ta suy ra vị trí tương đối của hai đường thẳng
Giao điểm của hai đường thẳng d1 và d2 ( nếu có ) là nghiệm hệ phương trình :
Nếu hệ phương trình trên có một nghiệm duy nhất thì 2 đường thẳng cắt nhau .
Nếu hệ phương trình trên có vô số nghiệm thì 2 đường thẳng trùng nhau .
Nếu hệ phương trình trên vô nghiệm thì 2 đường thẳng song song .
Các dạng toán về phương trình đường thẳng
Dạng 1 : Viết PT đường thẳng ( d ) qua 1 điểm và có VTCP
– Điểm M0(x0;y0;z0), VTCP 
* Phương pháp :
– Phương trình tham số của ( d ) là :
– Nếu a. b. c ≠ 0 thì ( d ) có PT chính tắc là :
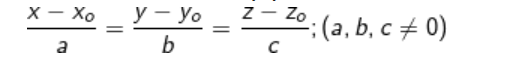
Ví dụ: Viết phương trình đường thẳng (d) đi qua điểm A(1;2;-1) và nhận vec tơ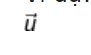 
(1;2;3) làm vec tơ chỉ phương.
* Lời giải :
– Phương trình tham số của ( d ) là :
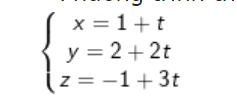
Dạng 2 : Viết PT đường thẳng đi qua 2 điểm A, B
* Phương pháp
– Bước 1 : Tìm VTCP
– Bước 2: Viết PT đường thẳng (d) đi qua A và nhận 
làm VTCP .
Ví dụ : Viết PTĐT ( d ) đi qua những điểm A ( 1 ; 2 ; 0 ), B ( – 1 ; 1 ; 3 ) ;
* Lời giải :
– Ta có :
(-2;-1;3)
– Vậy PTĐT ( d ) đi qua A có VTCP là
có PT tham số :
Dạng 3 : Viết PT đường thẳng đi qua A và song song với đường thẳng Δ
* Phương pháp
– Bước 1 : Tìm VTCP
– Bước 2 : Viết PT đường thẳng ( d ) đi qua A và nhận vecto u làm vecto chỉ phương .
Ví dụ : Viết phương trình đường thẳng đi qua A ( 2 ; 1 ; – 3 ) và song song với đường thẳng Δ :
làm VTCP
– Phương trình tham số của ( d ) :
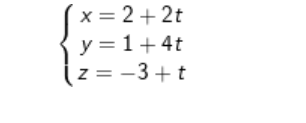
Dạng 4 : Viết PT đường thẳng ( d ) đi qua A và vuông góc với mp ( ∝ ) .
* Phương pháp
– Bước 1 : Tìm VTPT vecto n của mp ( ∝ )
– Bước 2 : Viết PT đường thẳng ( d ) đi qua A và nhận vecto n làm vecto chỉ phương .
Bài tập áp dụng phương trình đường thẳng
Bài tập 1 : Viết phương trình đường thẳng đi qua hai điểm A ( 1 ; 2 ) và B ( 0 ; 1 ) .
Bài giải :
Gọi phương trình đường thẳng là d : y = ax + by = ax + b
Vì đường thẳng d đi qua hai điểm A và B nê n ta có :
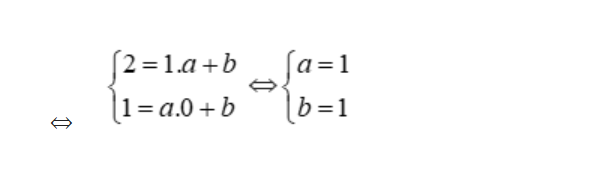
Thay a = 1 và b = 1 vào phương trình đường thẳng d thì d là : y = x + 1
Vậy phương trình đường thẳng đi qua 2 điểm A và B là : y = x + 1
Bài tập 2 : Cho Parabol ( P ) : y = – × ². Viết phương trình đường thẳng đi qua hai điểm A và B biết A và B là hai điểm thuộc ( P ) và có hoành độ lần lượt là 1 và 2 .
Bài giải
Với bài toán này chúng ta chưa biết được tọa độ của A và B là như nào. Tuy nhiên bài toán lại cho A và B thuộc (P) và có hoành độ rồi. Chúng ta cần đi tìm tung độ của điểm A và B là xong.
Tìm tọa độ của A và B :
Vì A có hoành độ bằng – 1 và thuộc ( P ) nên ta có tung độ y = − ( 1 ) ² = – 1 => A ( 1 ; − 1 )
Bài viết trên đã gửi đến bạn triết lý cũng như những bài tập về phương trình đường thẳng. Hy vọng bài viết trên hoàn toàn có thể giúp ích được cho bạn trong việc giải bài tập. Phương trình đường thẳng là nhu yếu của rất nhiều bài tập cũng như trong đề thi nên những bạn hãy quan tâm nhé !
Source: http://wp.ftn61.com
Category: Hỏi Đáp
Để lại một bình luận