Phương trình đường vuông góc chung

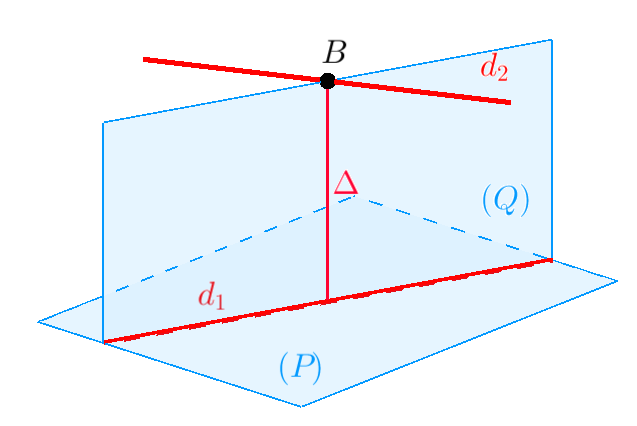
Hình 1. Đường vuông góc chung

Đường vuông góc chung.

Trong không gian cho hai đường thẳng chéo nhau $d_1$ và $d_2$. Khi đó tồn tại đường thẳng $\Delta$ vuông góc và cắt cả hai đường thẳng $d_1$ và $d_2$.

Cách dựng đoạn vuông góc chung .

Bước 1. Dựng mặt phẳng $\left( P \right)$ chứa $d_1$ và song song với $d_2$.
Bước 2. Dựng mặt phẳng $\left( Q \right)$ chứa $d_1$ và vuông góc với $\left( P \right)$.
Bước 3. Tìm giao điểm $B = {d_2} \cap \left( Q \right).$ Đường vuông góc chung $\Delta$ đi qua $B$ và vuông góc với $\left( P \right)$.

Viết phương trình đường vuông góc chung trong khoảng trống – Cách 1. Cũng chính là cách dựng. Trong không gian $Oxyz$ giả sử đường thẳng $d_1$, $d_2$ lần lượt có vector chỉ phương là ${{\vec u}_1},{{\vec u}_2}$.

Bước 1. Viết phương trình mặt phẳng $\left( P \right)$ chứa $d_1$ và song song với $d_2$. Cặp vector chỉ phương của $\left( P \right)$ là ${{\vec u}_1},{{\vec u}_2}$. Suy ra $${\vec n_P} = \left[ {{{\vec u}_{{d_1}}},{{\vec u}_{{d_2}}}} \right].$$
Bước 2. Viết phương trình mặt phẳng $\left( Q \right)$ chứa $d_1$ và vuông góc với $\left( P \right)$. Cặp vector chỉ phương của $\left( Q \right)$ là ${{{\vec u}_{{d_1}}},{{\vec n}_P}}$. Suy ra $${\vec n_Q} = \left[ {{{\vec u}_{{d_1}}},{{\vec n}_P}} \right].$$
Bước 3. Tìm giao điểm $B = {d_2} \cap \left( Q \right).$ Viết phương trình đường vuông góc chung $\Delta$ đi qua $B$ và vuông góc với $\left( P \right)$.

Bạn đang đọc: Phương trình đường vuông góc chung

Ví dụ 1.

Viết phương trình đường vuông góc chung của $\left( {{d_1}} \right):\left\{ \begin{array}{l}
x = t\\
y = 5 – 2t\\
z = 14 – 3t
\end{array} \right.$ và $\left( {{d_2}} \right):\left\{ \begin{array}{l}
x = 9 – 4\lambda \\
y = 3 + \lambda \\
z = – 1 + 5\lambda
\end{array} \right..$
Giải. Gọi mặt phẳng $\left( P \right)$ chứa $d_1$ và song song với $d_2$. Khi đó cặp vector chỉ phương của $\left( P \right)$ là ${{\vec u}_{{d_1}}} = \left( {1; – 2; – 3} \right),\;\;{{\vec u}_{{d_2}}} = \left( { – 4;1;5} \right)$. Suy ra ${\vec n_P} = \left[ {{{\vec u}_{{d_1}}},{{\vec u}_{{d_2}}}} \right] = \left( { – 7;7; – 7} \right) = – 7\left( {1; – 1;1} \right).$
Chọn $M\left( {0;5;14} \right) \in {d_1} \subset \left( P \right).$ Phương trình mặt phẳng $\left( P \right)$ là $$\left( P \right):1 \cdot \left( {x – 0} \right) – 1 \cdot \left( {y – 5} \right) + 1 \cdot \left( {z – 14} \right) = 0 \Leftrightarrow x – y + z – 9 = 0.$$ Gọi $\left( Q \right)$ chứa $d_1$ và vuông góc với $\left( P \right)$. Cặp vector chỉ phương của $\left( Q \right)$ là ${{\vec u}_1} = \left( {1; – 2; – 3} \right),\;{{\vec n}_P} = \left( {1; – 1;1} \right)$. Suy ra ${\vec n_Q} = \left[ {{{\vec u}_{{d_1}}},{{\vec n}_P}} \right] = \left( { – 5; – 4;1} \right).$ Mặt khác $M\left( {0;5;14} \right) \in {d_1} \subset \left( Q \right).$ Phương trình của mặt phẳng $\left( Q \right)$ là $$\left( Q \right): – 5 \cdot \left( {x – 0} \right) – 4 \cdot \left( {y – 5} \right) + 1 \cdot \left( {z – 14} \right) = 0 \Leftrightarrow – 5x – 4y + z + 6 = 0.$$ Gọi $B = {d_2} \cap \left( Q \right)$. Từ phương trình của $d_2$ và $\left( Q \right)$ ta được $ – 5\left( {9 – 4\lambda } \right) – 4\left( {3 + \lambda } \right) – 1 + 5\lambda – 9 = 0 \Leftrightarrow \lambda = \frac{{52}}{{21}}$. Thay $\lambda = \frac{{52}}{{21}}$ vào phương trình $d_2$ ta được $x = – \frac{{19}}{21};y = \frac{{115}}{{21}};z = \frac{{239}}{{21}} \Rightarrow B\left( { – \frac{{19}}{21};\frac{{115}}{{21}};\frac{{239}}{{21}}} \right).$
Đường thẳng $\Delta$ và vuông góc với $\left( P \right)$ nên

Xem Thêm Tổng bí thư Nguyễn Phú Trọng ‘đốt lò’ trong Hội nghị Trung ương 3

${{\vec u}_\Delta } = {{\vec n}_P} = \left( {1; – 1;1} \right)$

, và đi qua $ B $ nên có phương trình là

$$\left\{ \begin{array}{l}
x = – \frac{{19}}{21} + t\\
y = \frac{{115}}{{21}} – t\\
z = \frac{{239}}{{21}} + t
\end{array} \right.$$

Viết phương trình đường vuông góc chung trong khoảng trống – Cách 2 .Dùng quang hệ vuông góc.

Bước 1. Viết phương trình đường thẳng $d_1$ và $d_2$ dưới dạng tham số.

$$\left( {{d_1}} \right):\left\{ \begin{array}{l}
x = {x_1} + {a_1}t\\
y = {y_1} + {b_1}t\\
z = {z_1} + {c_1}t
\end{array} \right.{\rm{ }}\left( {{d_2}} \right):\left\{ \begin{array}{l}
x = {x_2} + {a_2}\lambda \\
y = {y_2} + {b_2}\lambda \\
z = {z_2} + {c_2}\lambda
\end{array} \right.{\rm{ }}$$
Bước 2. Giả sử $A = {d_1} \cap \Delta ,{\rm{ }}B = {d_2} \cap \Delta .$ $$\begin{array}{l}
A \in {d_1} \Rightarrow A\left( {{x_1} + {a_1}t,{y_1} + {b_1}t,{z_1} + {c_1}t{\rm{ }}} \right),\\
B \in {d_2} \Rightarrow B\left( {{x_2} + {a_2}\lambda ,{y_2} + {b_2}\lambda ,{z_2} + {c_2}\lambda } \right).
\end{array}$$
Bước 3. Dùng quan hệ vuông góc để tìm $A$ và $B$
$$\left\{ \begin{array}{l}
AB \bot {d_1}\\
AB \bot {d_2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} \bot {{\vec u}_{{d_1}}}\\
\overrightarrow {AB} \bot {{\vec u}_{{d_2}}}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
\overrightarrow {AB} \cdot {{\vec u}_{{d_1}}} = 0\\
\overrightarrow {AB} \cdot {{\vec u}_{{d_2}}} = 0
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
t,A\\
\lambda ,B
\end{array} \right..$$

Ví dụ 2.

Xem thêm: Tại sao đọc truyện cổ tích tiếng anh là phương pháp được lựa chọn?

Giải. Gọi $\Delta$ là đường vuông góc chung của $d_1$ và $d_2$. Giả sử $A = {d_1} \cap \Delta ,{\rm{ }}B = {d_2} \cap \Delta .$
Ta có $A \in {d_1} \Rightarrow A\left( {t;5 – 2t;14 – 3t{\rm{ }}} \right),B \in {d_2} \Rightarrow B\left( {9 – 4\lambda ;3 + \lambda ; – 1 + 5\lambda } \right).$
Suy ra $\overrightarrow {AB} = \left( {9 – 4\lambda – t; – 2 + \lambda + 2t; – 15 + 5\lambda + 3t} \right)$.
Vì $\overrightarrow {AB} \bot {d_1},\overrightarrow {AB} \bot {d_1}$ nên ta có

Xem Thêm " Cái Cân Tiếng Anh Là Gì - Cái Cân Trong Tiếng Anh Là Gì

$$\left\{ \begin{gathered}
\overrightarrow {AB} \cdot {{\vec u}_{{d_1}}} = 0 \hfill \\
\overrightarrow {AB} \cdot {{\vec u}_{{d_2}}} = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
1\left( {9 – 4\lambda – t} \right) – 2\left( { – 2 + \lambda + 2t} \right) – 3\left( { – 15 + 5\lambda + 3t} \right) = 0 \hfill \\
– 4\left( {9 – 4\lambda – t} \right) + \left( { – 2 + \lambda + 2t} \right) + 5\left( { – 15 + 5\lambda + 3t} \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\lambda = \frac{{52}}{{21}} \hfill \\
t = \frac{{3}}{7} \hfill \\
\end{gathered} \right..$$
Lần lượt thay

$t = \frac{{3}}{7},\lambda = \frac{{52}}{{21}}$ vào phương trình của USD d_1 USD và $ d_2 $ ta được$A\left( { \frac{{3}}{7};\frac{{29}}{7};\frac{{89}}{7}} \right)$ và $B\left( { – \frac{{19}}{{21}};\frac{{115}}{{21}};\frac{{239}}{{21}}} \right).$ Đường thẳng $\Delta$ qua $A$ và $B$ nên ${{\vec u}_\Delta } = \overrightarrow {AB} = \left( {-\frac{{4}}{{3}}; \frac{{4}}{{3}}; – \frac{4}{{3}}} \right)$ $= – \frac{4}{3}\left( {1; – 1;1} \right).$ Vì $\Delta$ qua $B$ nên có phương trình $$\left\{ \begin{array}{l}
x = – \frac{{19}}{21} + t\\
y = \frac{{115}}{{21}} – t\\
z = \frac{{239}}{{21}} + t
\end{array} \right.$$

Bài tập

(nhiều bài tập hơn khi đăng ký học tại Trung tâm Cùng học toán)

Xem thêm: Nước Úc Tiếng Anh Là Gì – Nước Úc Trong Tiếng Anh Là Gì

USD { { \ vec u } _ \ Delta } = { { \ vec n } _P } = \ left ( { 1 ; – 1 ; 1 } \ right ) USD

Source: http://wp.ftn61.com
Category: Hỏi Đáp