Giải Sách Bài Tập Toán 11 Bài 3: Một Số Phương Trình Lượng Giác Thường Gặp

Xem toàn bộ tài liệu Lớp 11: tại đây

Xem thêm các sách tham khảo liên quan:

Sách Giải Sách Bài Tập Toán 11 Bài 3 : Một số phương trình lượng giác thường gặp giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 11 sẽ giúp bạn rèn luyện năng lực suy luận hài hòa và hợp lý và hợp logic, hình thành năng lực vận dụng kết thức toán học vào đời sống và vào những môn học khác :

Bài 1.25 trang 37 Sách bài tập Đại số 11: Giải các phương trình sau

a) cos2x – sinx – 1 = 0

b ) cosx. cos2x = 1 + sinx. sin2x
c ) 4sinx.cosx. cos2x = – 1
d ) tanx = 3 cotx

Lời giải:

a ) cos2x – sinx – 1 = 0
⇔ 1 – 2 sin2x – sinx – 1 = 0
⇔ sinx ( 2 sinx + 1 ) = 0

b ) cosx. cos2x = 1 + sinx. sin2x
⇔ cosx. cos2x – sinx. sin2x = 1
⇔ cos3x = 1 ⇔ 3 x = k2π

c ) 4sinx.cosx. cos2x = – 1
⇔ 2 sin2x. cos2x = – 1
⇔ sin4x = – 1

d ) tanx = 3 cotx ( Điều kiện cosx ≠ 0 và sinx ≠ 0 )
Ta có :

Các phương trình này thỏa mãn nhu cầu điều kiện kèm theo của phương trình nên là nghiệm của phương trình đã cho .

Bài 1.26 trang 37 Sách bài tập Đại số 11: Giải các phương trình sau

a ) 3 cos2x – 2 sinx + 2 = 0
b ) 5 sin2x + 3 cosx + 3 = 0
c ) sin6x + cos6x = 4 cos22x
d ) – 0,25 + sin2x = cos4x

Lời giải:

a ) 3 cos2x – 2 sinx + 2 = 0
⇔ 3 ( 1 – sin2x ) – 2 sinx + 2 = 0
⇔ 3 sin2x + 2 sinx – 5 = 0
⇔ ( sinx – 1 ) ( 3 sinx + 5 ) = 0
⇔ sinx = 1
⇔ x = π / 2 + k2π, k ∈ Z
b ) 5 sin2x + 3 cosx + 3 = 0
⇔ 5 ( 1 – cos2x ) + 3 cosx + 3 = 0
⇔ 5 cos2x – 3 cosx – 8 = 0
⇔ ( cosx + 1 ) ( 5 cosx – 8 ) = 0
⇔ cosx = – 1
⇔ x = ( 2 k + 1 ) π, k ∈ Z
c ) sin6x + cos6x = 4 cos22x
⇔ ( sin2x + cos2x ) 3 – 3 sin2x. cos2x ( sin2x + cos2x ) = 4 cos22x

Bài 1.27 trang 37 Sách bài tập Đại số 11: Giải các phương trình sau

a ) 2 tanx – 3 cotx – 2 = 0 ;
b ) cos2x = 3 sin2x + 3 ;
c ) cotx – cot2x = tanx + 1 .

Lời giải:

a ) 2 tanx – 3 cotx – 2 = 0 ( Điều kiện cosx ≠ 0 và sinx ≠ 0 )
Ta có

Các giá trị này thỏa mãn nhu cầu điều kiện kèm theo nên là nghiệm của phương trình
b ) cos2x = 3 sin2x + 3
Ta thấy cosx = 0 không thỏa mãn nhu cầu phương trình. Với cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được :

c ) cotx – cot2x = tanx + 1 ( 1 )
Điều kiện : sinx ≠ 0 và cosx ≠ 0. Khi đó :

Các giá trị này thỏa mãn nhu cầu điều kiện kèm theo nên là nghiệm của phương trình

Bài 1.28 trang 38 Sách bài tập Đại số 11: Giải các phương trình sau

a ) cos2x + 2sinx.cosx + 5 sin2x = 2 ;
b ) 3 cos2x – 2 sin2x + sin2x = 1 ;
c ) 4 cos2x – 3sinx.cosx + 3 sin2x = 1 .

Lời giải:

a ) cos2x + 2sinx.cosx + 5 sin2x = 2
Rõ ràng cosx = 0 không thỏa mãn nhu cầu phương trình. Với cosx ≠ 0, chia hai vế cho cos2x ta được :
1 + 2 tanx + 5 tan2x = 2 ( 1 + tan2x )
⇔ 3 tan2x + 2 tanx – 1 = 0

b ) 3 cos2x – 2 sin2x + sin2x = 1
Với cosx = 0 ta thấy hai vế đều bằng 1. Vậy phương trình có nghiệm x = 0,5 π + kπ, k ∈ Z
Trường hợp cosx ≠ 0, chia hai vế cho cos2x ta được :
3 – 4 tanx + tan2x = 1 + tan2x
⇔ 4 tanx = 2

⇔ tanx = 0,5
⇔ x = arctan 0,5 + kπ, k ∈ Z
Vậy nghiệm của phương trình là x = 0,5 π + kπ, k ∈ Z và x = arctan 0,5 + kπ, k ∈ Z
c ) 4 cos2x – 3sinx.cosx + 3 sin2x = 1
Rõ ràng cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được :
4 – 3 tanx + 3 tan2x = 1 + tan2x
⇔ 2 tan2x – 3 tanx + 3 = 0
Phương trình cuối vô nghiệm so với tanx, do đó phương trình đã cho vô nghiệm

Bài 1.29 trang 38 Sách bài tập Đại số 11: Giải các phương trình sau

a ) 2 cosx – sinx = 2 ;
b ) sin5x + cos5x = – 1 ;
c ) 8 cos4x – 4 cos2x + sin4x – 4 = 0 ;
d ) sin6x + cos6x + sin4x / 2 = 0 .

Lời giải:

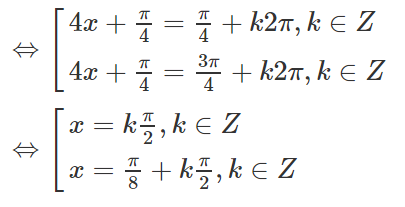
Bài 1.30 trang 38 Sách bài tập Đại số 11: Giải các phương trình sau:

Lời giải:

a ) 1 + sinx – cosx – sin2x + 2 cos2x = 0 ( 1 )
Ta có :
1 – sin2x = ( sinx – cosx ) 2
⇔ 2 cos2x = 2 ( cos2x – sin2x ) = – 2 ( sinx – cosx ) ( sinx + cosx )
Vậy ( 1 ) ⇔ ( sinx – cosx ) ( 1 + sinx – cosx – 2 sinx – 2 cosx ) = 0
⇔ ( sinx – cosx ) ( 1 – sinx – 3 cosx ) = 0

Điều kiện sinx ≠ 0

( thỏa mãn nhu cầu điều kiện kèm theo )
c ) cosx. tan3x = sin5x
Điều kiện : cos3x ≠ 0. Khi đó ,
( 3 ) ⇔ cosx. sin3x = cos3x. sin5x

Kết hợp với điều kiện kèm theo ta được nghiệm của phương trình là :

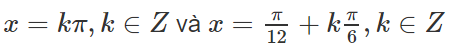
d ) 2 tan2x + 3 tanx + 2 cot2x + 3 cotx + 2 = 0 ( 4 )
Điều kiện : cosx ≠ 0 và sinx ≠ 0. Khi đó ,
( 4 ) ⇔ 2 ( tan2x + cot2x ) + 3 ( tanx + cotx ) + 2 = 0 ⇔ 2 [ ( tanx + cotx ) 2 − 2 ] + 3 ( tanx + cotx ) + 2 = 0
Đặt t = tanx + cotx ta được phương trình
2 t2 + 3 t − 2 = 0 ⇒ t = − 2, t = 0,5
Với t = – 2 ta có tanx + cotx = – 2
⇔ tan2x + 2 tanx + 1 = 0 ⇒ tanx = − 1 ⇒ x = − π / 4 + kπ, k ∈ Z
( thỏa mãn nhu cầu điều kiện kèm theo )
Với t = 0,5 ta có tanx + cotx = 0,5 ⇔ 2 tan2x − tanx + 2 = 0
Phương trình này vô nghiệm .
Vậy nghiệm của phương trình ( 4 ) là x = − π / 4 + kπ, k ∈ Z

Bài 1.31 trang 38 Sách bài tập Đại số 11: Giải phương trình cotx – tanx + 4sin2x = 2/sin2x

Lời giải:

Đối với những phương trình lượng giác chứa tanx, cotx, sin2x hoặc cos2x, ta hoàn toàn có thể đưa về phương trình chứa cosx, sinx, sin2x, hoặc cos2x ngoài những cũng hoàn toàn có thể đặt ẩn phụ t = tanx để đưa về một phương trình theo t .
Cách 1 : Điều kiện của phương trình :
sin2x ≠ 0 ⇔ cos2x ≠ 1 hoặc cos2x ≠ – 1 ( 1 )
Ta có :

Cách 2. Đặt t = tanx
Điều kiện t ≠ 0

Phương trình đã cho có dạng

Bài tập trắc nghiệm trang 38, 39 Sách bài tập Đại số 11:

Bài 1.32: Nghiệm của phương trình 3cotx – √3 = 0 là:

Lời giải:

Ta có cotx = 1 / √ 3 ⇒ x = π / 3 + kπ, k ∈ Z .

Chọn đáp án: B

Bài 1.33: Nghiệm của phương trình sin4x – cos4x = 0 là

Lời giải:

Ta có sin4 x – cos4 x = 0 ⇔ ( sin2 x + cos2x ) ( sin2 x – cos2 x ) = 0
⇔ sin2 x – cos2x = 0 ⇔ cos2x = 0 ⇔ 2 x = π / 2 + kπ ⇔ x = π / 4 + kπ / 2 .

Chọn đáp án: C

Bài 1.34: Cho phương trình 4cos22x + 16sinx.cosx – 7 = 0 (1)

Xét những giá trị

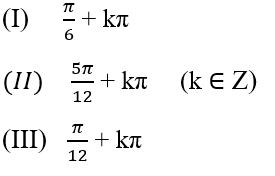
Trong những giá trị trên, giá trị nào là nghiệm của phương trình ( 1 ) ?
A. Chỉ ( I ) B. Chỉ ( II )
C. Chỉ ( III ) D. Chỉ ( II ) và ( III )

Lời giải:

Ta có ( 1 ) ⇔ 4 ( 1 – sin2 2 x ) + 8 sin2x – 7 = 0 ⇔ 4 sin2 2 x – 8 sin2x + 3 = 0

Chọn đáp án: D

Bài 1.35: Nghiệm của phương trình cosx.cos7x = cos3x.cos5x là

Lời giải:

Ta có : cosx. cos7x = cos3x. cos5x
⇔ cos8x + cos6x = cos8x + cos2x ⇔ cos6x = cos2x ⇔ 6 x = ± 2 x + k2π .

Vì tập hợp giá trị kπ / 4 bao tập những giá trị kπ / 2 nên nghiệm của phương trình là kπ / 4, k ∈ Z .

Chọn đáp án:

Bài 1.36: Nghiệm của phương trình 3tan2x + 6cotx = -tanx là

Lời giải:

Điều kiện của phương trình :
x ≠ kπ, x ≠ π / 2 + kπ, x ≠ π / 4 + kπ / 2 ( k ∈ Z )
Xét những giải pháp .
– Vì π / 4 và π / 2 không thỏa mãn nhu cầu điều kiện kèm theo của phương trình nên hai giải pháp A và D bị loại .
– Với x = π / 6 thì vế phải của phương trình đã cho âm, còn vế trái dương, nên giải pháp C bị loại .

Chọn đáp án: B

Bài 1.37: Nghiệm của phương trình 2sinx = 3cotx là

Lời giải:

Điều kiện của phương trình : x ≠ kπ ( k ∈ Z )
Cách 1. Giải trực tiếp .
Biến đổi phương trình đã cho ta được

Cách 2. Xét những giải pháp .
– Với x = π / 6 thì vế trái của phương trình bằng 1, còn vế phải là 3 √ 3 nên giải pháp A bị loại .
– Giá trị kπ / 2 với k = 2 không thỏa mãn nhu cầu điều kiện kèm theo của phương trình nên giải pháp B bị loại .
– Với x = π / 4 thì vế trái của phương trình bằng √ 2, còn vế phải bằng 3, nên giải pháp C bị loại .

Chọn đáp án: D

Bài 1.38: Cho phương trình √3.cosx + sinx = 2(∗)

Xét những giá trị

Trong những giá trị trên, giá trị nào là nghiệm của phương trình ( ∗ )
A. Chỉ ( I ) B. Chỉ ( II )
C. Chỉ ( III ) D. Chỉ ( I ) và ( III )

Lời giải:

Ta có (*) ⇔ 2(√3/2 cosx+ 1/2 sinx) = 2

⇔ cos ( x – π / 6 ) = 1 ⇔ x = π / 6 + k2π, k ∈ Z.

Chọn đáp án: C

Bài tập trắc nghiệm

Bài tập trắc nghiệm

Bài tập trắc nghiệm

Bài tập trắc nghiệm

Source: http://wp.ftn61.com
Category: Hỏi Đáp