Công thức giải phương trình lượng giác cơ bản chi tiết nhất – Toán lớp 11

Với Công thức giải phương trình lượng giác cơ bản Toán lớp 11 chi tiết cụ thể nhất giúp học viên thuận tiện nhớ hàng loạt những công thức giải phương trình lượng giác cơ bản từ đó biết cách làm bài tập Toán 11. Mời những bạn đón xem :

Công thức giải phương trình lượng giác cơ bản chi tiết nhất – Toán lớp 11

1. Lí thuyết

* Công thức nghiệm cơ bản

a ) Phương trình sin x = m
Trường hợp 1 : | m | > 1. Phương trình vô nghiệm .
Trường hợp 2 : m ≤ 1. Phương trình có nghiệm .
– Nếu m trình diễn được dưới dạng sin của những góc đặc biệt quan trọng thì :
sinx = m ⇔ sinx = sinα ⇔ x = α + k2πx = π − α + k2πk ∈ ℤ
– Nếu m không trình diễn được dưới dạng sin của những góc đặc biệt quan trọng thì :
sinx = m ⇔ x = arcsinm + k2πx = π − arcsinm + k2πk ∈ ℤ
– Các trường hợp đặc biệt quan trọng :
sinx = 0 ⇔ x = kπk ∈ ℤsinx = 1 ⇔ x = π2 + k2πk ∈ ℤsinx = − 1 ⇔ x = − π2 + k2πk ∈ ℤ
b ) Phương trình cos x = m
Trường hợp 1 : | m | > 1. Phương trình vô nghiệm .
Trường hợp 2 : m ≤ 1. Phương trình có nghiệm .
– Nếu m trình diễn được dưới dạng cos của những góc đặc biệt quan trọng thì :
cosx = m ⇔ cosx = cosα ⇔ x = α + k2πx = − α + k2πk ∈ ℤ
– Nếu m không trình diễn được dưới dạng cos của những góc đặc biệt quan trọng thì :
cosx = m ⇔ x = arccosm + k2πx = − arccosm + k2πk ∈ ℤ
– Các trường hợp đặc biệt quan trọng :
cosx = 0 ⇔ x = π2 + kπk ∈ ℤcosx = 1 ⇔ x = k2πk ∈ ℤcosx = − 1 ⇔ x = π + k2πk ∈ ℤ
c ) Phương trình : tan x = m. Điều kiện : x ≠ π2 + kπk ∈ ℤ
– Nếu m trình diễn được dưới dạng tan của những góc đặc biệt quan trọng thì :
tanx = m ⇔ tanx = tanα ⇔ x = α + kπk ∈ ℤ
– Nếu m không màn biểu diễn được dưới dạng tan của những góc đặc biệt quan trọng thì :
tanx = m ⇔ x = arctanm + kπk ∈ ℤ
d ) Phương trình : cot x = m. Điều kiện : x ≠ kπk ∈ ℤ
– Nếu m trình diễn được dưới dạng cot của những góc đặc biệt quan trọng thì :
cotx = m ⇔ cotx = cotα ⇔ x = α + kπk ∈ ℤ
– Nếu m không màn biểu diễn được dưới dạng cot của những góc đặc biệt quan trọng thì :
cotx = m ⇔ x = arccotm + kπk ∈ ℤ
* Mở rộng công thức nghiệm, với u ( x ) và v ( x ) là hai biểu thức của x .

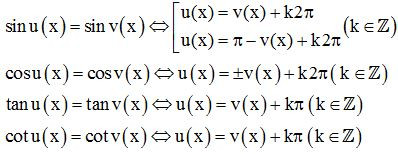
2. Công thức

Khi đã cho số m, ta hoàn toàn có thể tìm những giá trị arcsin m, arccos m, arctan m, arccot m bằng máy tính bỏ túi với những phím sin-1 ; cos-1 ; tan-1 .
Bước 1. Chỉnh chính sách rad hoặc độ
– Muốn tìm số đo radian :
ta ấn qw4 ( so với Casio fx – 570VN )
ta ấn qw22 ( so với Casio fx – 580VN X )
– Muốn tìm số đo độ :
ta ấn qw3 ( so với Casio fx – 570VN )
ta ấn qw21 ( so với Casio fx – 580VN X )
Bước 2. Tìm số đo góc
Tìm góc α khi biết sin của góc đó bằng m, ta ấn lần lượt qj m = .
Tương tự so với cos và tan .
Chú ý : Muốn tìm góc α khi biết cot của góc đó bằng m, ta ấn lần lượt ql1a m USD ) = .
Sau đó vận dụng công thức lượng giác để giải phương trình .

3. Ví dụ minh họa

Ví dụ 1: Giải phương trình sau:

a ) sinx = 22
b ) cosx − π3 = 12

c) cot2x=3

Lời giải

a ) sinx = 22
⇔ sinx = sinπ4 ( Bấm máy SHIFT + SIN + 22 )
⇔ x = π4 + k2πx = 3 π4 + k2πk ∈ ℤ
Vậy họ nghiệm của phương trình là : x = π4 + k2π ; x = 3 π4 + k2π ; k ∈ ℤ .
b ) cosx − π3 = 12
⇔ cosx − π3 = cosπ3 ( Bấm máy SHIFT + COS + 12 )
⇔ x − π3 = π3 + k2πx − π3 = − π3 + k2π ⇔ x = 2 π3 + k2πx = k2πk ∈ ℤ
Vậy họ nghiệm của phương trình là : x = 2 π3 + k2π ; x = k2π ; k ∈ ℤ .
c ) cot2x = 3
Điều kiện xác lập : sin2x ≠ 0 ⇔ 2 x ≠ kπ ⇔ x ≠ kπ2k ∈ ℤ .
Ta có cot2x = cotπ6 ( Bấm máy SHIFT + Tan + 13 )
⇔ 2 x = π6 + kπ
⇔ x = π12 + kπ2k ∈ ℤ ( Thỏa mãn điều kiện kèm theo xác lập )
Vậy họ nghiệm của phương trình là : x = π12 + kπ2 ; k ∈ ℤ .

Ví dụ 2: Giải phương trình sau:

a ) cos2x − π3 = cosx + π6
b ) tan3x + π4 = tanx

Lời giải

a ) cos2x − π3 = cosx + π6
⇔ 2 x − π3 = x + π6 + k2π2x − π3 = − x − π6 + k2π ⇔ x = π2 + k2π3x = π6 + k2π ⇔ x = π2 + k2πx = π18 + k2π3k ∈ ℤ
Vậy họ nghiệm của phương trình là : x = π2 + k2π ; x = π18 + k2π3 ; k ∈ ℤ .
b ) Điều kiện xác lập :
cos3x + π4 ≠ 0 cosx ≠ 0 ⇔ 3 x + π4 ≠ π2 + kπx ≠ π2 + kπ ⇔ x ≠ π12 + kπ3x ≠ π2 + kπk ∈ ℤ
Ta có : tan3x + π4 = tanx
⇔ 3 x + π4 = x + kπ ⇔ 2 x = − π4 + kπ
⇔ x = − π8 + kπ2k ∈ ℤ ( Thỏa mãn điều kiện kèm theo xác lập )
Vậy họ nghiệm của phương trình là : x = − π8 + kπ2 ; k ∈ ℤ .

4. Bài tập tự luyện

Câu 1. Phương trình lượng giác 2cosx2+3=0 có nghiệm là

A. x=±5π6+k2π;k∈ℤ

B. x=±5π3+k2π;k∈ℤ

C. x=±5π3+k4π;k∈ℤ

D. x=±5π6+k4π;k∈ℤ

Câu 2. Phương trình sinx+π4=1 có bao nhiêu nghiệm thuộc đoạn π;2π?

A. 0

B. 1

C. 2

D. 3

Câu 3. Cho phương trình cot3x=cot(x+3). Nghiệm của phương trình là:

A. 32+kπ;k∈ℤ

B. 32+kπ2;k∈ℤ

C. −32+kπ;k∈ℤ

D. −32+kπ2;k∈ℤ

Đáp án:

1 – C, 2 – A, 3 – B

Xem thêm tổng hợp công thức môn Toán lớp 9 đầy đủ và chi tiết khác:

Công thức, cách biến hóa biểu thức a sinx + b cosx

Công thức, cách gộp nghiệm phương trình lượng giác

Công thức hoán vị
Công thức chỉnh hợp
Công thức tổng hợp

Source: http://wp.ftn61.com
Category: Hỏi Đáp